一:定义
首先回忆一下二分法,猜一个100以内的整数,先从50开始,然后获得结果,结果有三种,大,小,相等;我们忽略结果,考虑过程,那就只有大和小,类似的还有true or false,等等两种走向的分支都可以用二叉树来描述.
1.二叉树的每个节点最多有2个子节点.
2.二叉树是有序树,左右子节点有顺序,左右子树自然也是有顺序的.
3.即使只有一个子节点,也是区分左右的.
二叉树的五种基本形态:
1.空树;
2.只有一个根节点;
3.根节点和左子树;
4.根节点和右子树;
5.根节点和左子树和右子树.
特殊的二叉树:
1.斜树,所有节点只有左子树的叫做左斜树,相反叫右斜树;
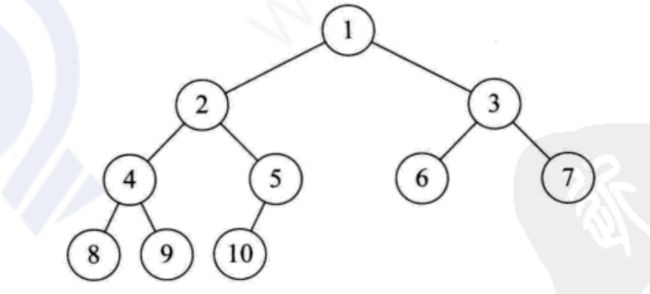
2.满二叉树:所有的节点都有左右子树,所有的叶节点都在同一层,也就是说每个节点左右子树节点都相等,是对称的.
3.完全二叉树:二叉树按层编号,从上到下从左到右,如果满足满二叉树的子集,那么称为完全二叉树
总结一些完全二叉树的特点:
叶节点一定在最下面两层
最下层的叶节点一定在左边
倒数第二层的叶节点一定在右边
如果度是1,那就只有左子树
完全二叉树不一定是满二叉树,满二叉树一定是完全二叉树,包含关系
二:二叉树的性质
首先满二叉树每一层节点数是等比数列,因此:
1.第i层的节点数<=2ⁱ⁻¹个;
2.深度为k的二叉树节点数<=2ᴷ - 1个;
其次:
3.对与任何一个二叉树T,总节点数n,其中叶节点个数为n₀,度为1的节点数为n₁,度为2的节点数为n₂;
因此n=n₀+n₁+n₂;
分支总数s = n-1 = n₀+n₁+n₂-1 = n₁+2*n₂,因此得到n₀=n₂+1.
另外对于完全二叉树:
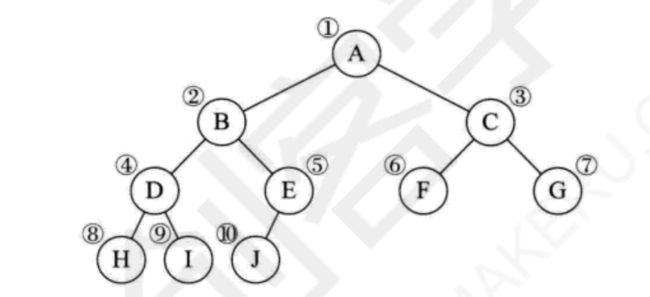
一个节点总数为n的完全二叉树,深度为
如果i=1,则是根节点;如果i>1,那么i的父节点是;
如果2i>n,则i没有孩子;否则i的左孩子是2i;
如果2i+1>n,则i没有右孩子,否则i的右孩子是2i+1;
三:二叉树存储结构
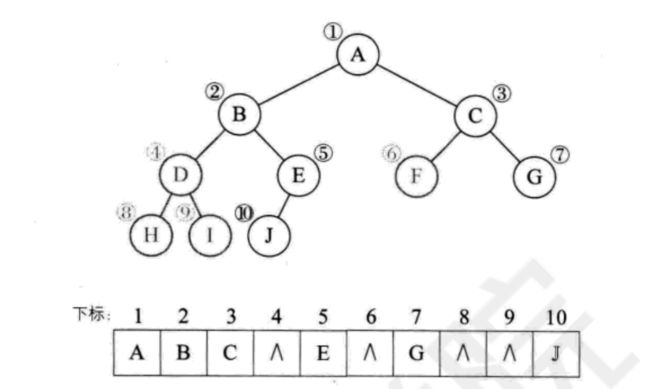
1.顺序存储
对于完全二叉树,我们把节点存储在数组中
可以看到由于完全二叉树的性质,即使顺序存储也能体现出来.
但是如果不是完全二叉树,可以选择把没有孩子的地方空出来,虽然会有空间的浪费,如果是一个所有节点都只有右孩子的二叉树,深度是k的同时节点数也是k,缺需要分配2ᴷ-1个空间.
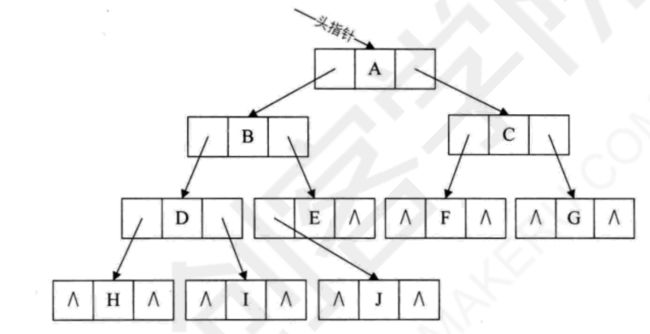
2.二叉链表
二叉树固定0~2个孩子,整个树都是可以分解成这个结构,因此定义一个这样的结构来表示节点,数据域,左孩子的指针域和右孩子指针域.
四:遍历二叉树
既然是遍历,那就得雨露均沾每个节点都要访问,而且每个节点还只能访问一次.
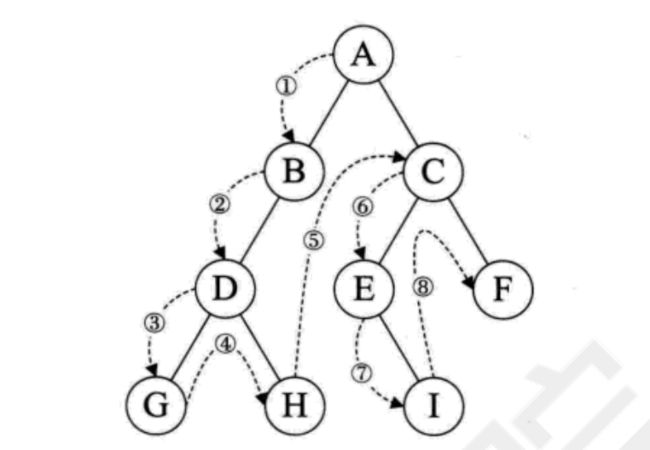
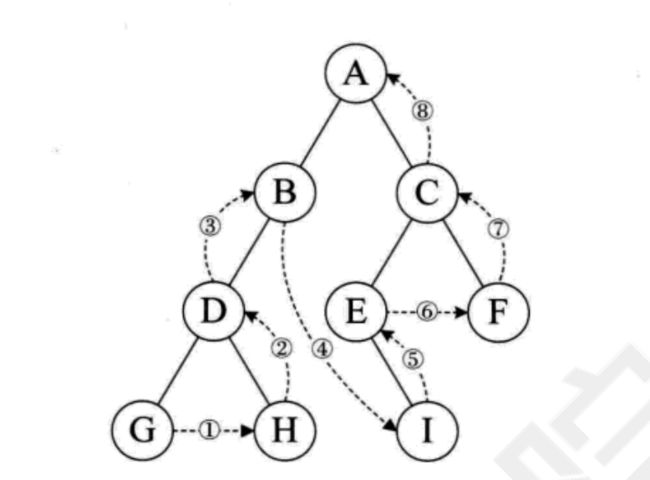
1.前序遍历
父节点 -> 左孩子 -> 右孩子
从根节点开始,先到达根节点的左孩子,然后左孩子的左孩子,一直到叶节点,接着是叶节点的兄弟,然后向上回溯,找到右孩子,重复这个过程.
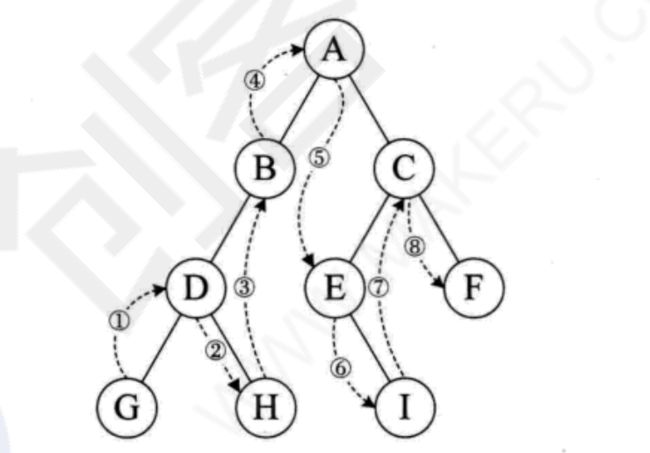
2.中序遍历
左孩子 -> 父节点 -> 右孩子
从最左边的叶节点开始,然后父节点,然后右孩子,然后到父节点的右兄弟,一路回到根节点,接着是右子树,重复这个过程.
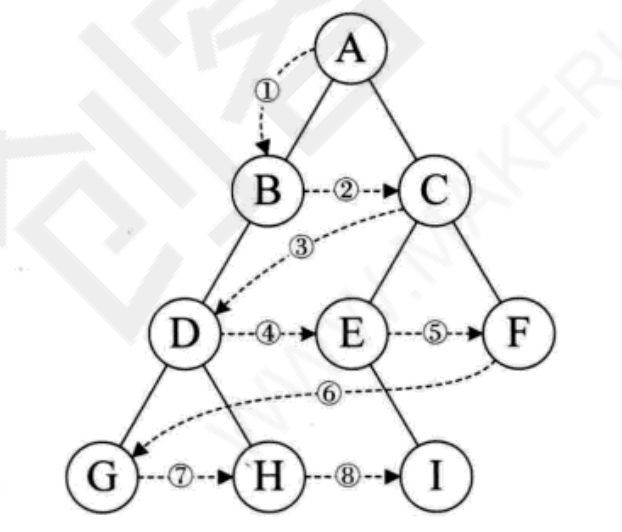
3.后序遍历
左孩子 -> 右孩子 -> 父节点
后序遍历关键在于兄弟节点,首先从最左边的叶节点开始,然后兄弟节点,然后回到父节点,然后是父节点的右兄弟,重复之前的过程.
4.层序遍历
简单直接,从上到下从左到右
五:算法实现
1.使用递归实现前序遍历
当节点访问左孩子的时候,左孩子再去访问左孩子,一直到子节点,函数才会返回,之后再访问右孩子,右孩子又是继续访问左孩子,一直到叶节点.
swift实现
//首先定义节点,节点有数据域,和两个孩子指针
class Node{
var name : String
var leftChild : Node?
var rightChild : Node?
init(_ dataName:String) {
name = dataName
}
}
//定义遍历的方法,如果没有孩子,则函数返回,如果有,就输出,然后继续访问孩子
func binaryTreeForEach(_ root : Node?){
guard let node = root else {
return
}
print(node.name)
binaryTreeForEach(node.leftChild)
binaryTreeForEach(node.rightChild)
}
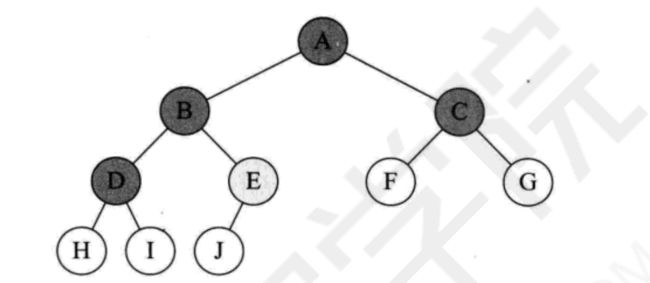
//然后组织一个二叉树,简化一下直接手写一个
let n1 = Node.init("A")
let n2 = Node.init("B")
let n3 = Node.init("C")
let n4 = Node.init("D")
let n5 = Node.init("E")
let n6 = Node.init("F")
let n7 = Node.init("G")
let n8 = Node.init("H")
let n9 = Node.init("I")
let n10 = Node.init("J")
n1.leftChild = n2
n1.rightChild = n3
n2.leftChild = n4
n4.rightChild = n5
n3.leftChild = n6
n3.rightChild = n7
n6.rightChild = n8
n7.leftChild = n9
n7.rightChild = n10
//调用函数
binaryTreeForEach(n1)
这个二叉树结构是这样的
_______A
____B_____C
_D______F___G
__E____H___I__J
总结前序遍历是父(左)(右),其中左可以递归(父(左)(右)),得到父(父(左)(右))(右),最左边一定是根节点,最右边是右孩子
2.使用递归实现中序遍历
通过递归可以发现,第一个被调用的,不一定是第一个被处理的,因此运用递归的特性,虽然中序遍历从叶节点开始,但是函数入口依然是根节点.
当节点访问完了左孩子时,输出并返回
swift实现(还是上面的那个二叉树
func binaryTreeForEach(_ root : Node?){
guard let node = root else {
return
}
binaryTreeForEach(node.leftChild)
print(node.name)
binaryTreeForEach(node.rightChild)
}
可见就改了一行代码,调换了输出位置.
总结中序遍历是(左)父(右),递归之后是((左)父(右))父(右),最左边是左孩子或者父节点,最右边是右孩子或父节点
3.用递归实现后续遍历
到这里就可以明白了,肯定是把输出放到最后去,当节点访问完了左右孩子时,函数输出并返回
swift实现
func binaryTreeForEach(_ root : Node?){
guard let node = root else {
return
}
binaryTreeForEach(node.leftChild)
binaryTreeForEach(node.rightChild)
print(node.name)
}
总结中序遍历是(左)(右)父,递归是((左)(右)父)(右)父,最右边一定是根节点.
- 根据遍历推导二叉树的结构,例如一个二叉树前序遍历是ABCDEF,中序遍历是CBAEDF,那么它的后序遍历是什么:
首先根节点是A;
BC可能性很多但是B一定在左或者在C上面,CB可以是C左B父,也可以C父B右,BC和CB结合起来答案是B是父节点,C是左孩子;
CBA可见回到了根节点A,那么EDF自然是右子树,同理DEF可以看出D是父节点,那么根据EDF得知E是左孩子F是右孩子.
二叉树结构如下
______A
___B_____D
C_____E____F
那么后序遍历顺序是CBEFDA.
根据中序遍历,我们能分出那些可能是左子树,那些可能是右子树,再根据前序后续就可以推断出二叉树,因此:
前序+中序或者后序+中序可以推断二叉树,而前序+后序不行
六:生成二叉树
遍历二叉树得到了一个序列,那么反过来遍历这个序列就可以生成二叉树.
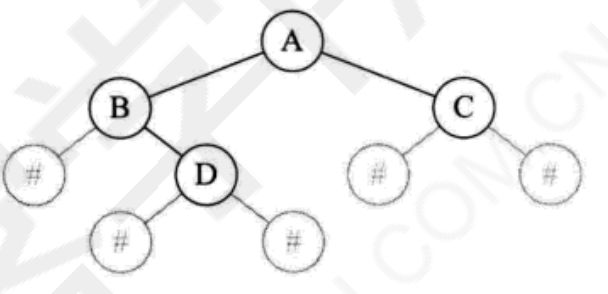
因此,给定一个序列和遍历方法,可以生成二叉树,但是只是这样还不行,因为经常不能确定是左孩子还是右孩子,因此要把每个节点的左右孩子都占位补满,叫做扩展,比如用特殊符号占位"AB#D##C##"
swift也是利用递归来实现
//调用
let node = createBinaryTree(["A","B","#","D","#","#","C","#","#"])
//正序遍历输出
binaryTreeForEach(node)
//实现
func createBinaryTree(_ list:[String]) -> Node?{
if(list.count == 0){
return nil
}
var index = 0
func createTree() -> Node?{
let str = list[index]
var tree : Node?
index += 1;
if index < list.count && str != "#"{
tree = Node.init(str)
tree!.leftChild = createTree()
tree!.rightChild = createTree()
}
return tree
}
return createTree()
}
扩展后的先序遍历可以确定一个二叉树,但是中序遍历不行,中序遍历一定会出现#..#..#..#..#..#的情况.