LeetCode刷题 最长递增子序列

LeetCode上最长递增子序列，中等难度记录下解题思路

这是一道LIS题目，LIS（Longest Increasing Subsequence）最长上升（不下降）子序列。

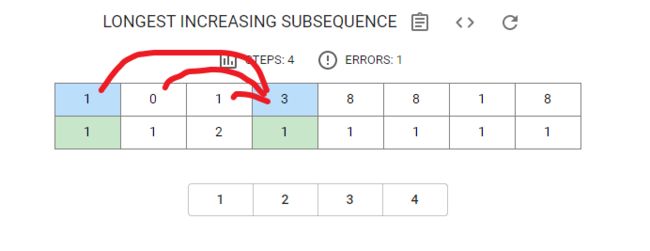
假设传入一个数组nums = [1,0,1,3,8,8,1,8]从i = 0开始取子数组，要计算能取到的最长递增子数组
这里开始引入动态规划的概念，拥有一个数组dp，dp中的dp[i]对应的是i位置的数组能获取的最长递增数组

这里发现了一个不错的线上LIS演示网站，结合这个网站来看整个过程

通过内外两层循环来解题外层循环i和内层循环j
例如

当求i = 3 nums[3] = 3的情况，需要遍历[0,3-1]的数和3对比
对比j= 0 nums[0] = 1和i = 3 nums[3] = 3的情况
3 > 1所以这个子串是能够成立的，并且由于dp[0] = 1，那么当j= 0 i =3的情况下最大的子串为Math.max(dp[i],dp[j]+1) 此时dp[3] = 2，之后j++
对比j= 1 nums[1] = 0和i = 3 nums[3] = 3的情况
3 > 0，但此时Math.max(dp[i],dp[j]+1) = Math.max(2,1+1)此时还是dp[3] = 2
对比j= 2 nums[2] = 1和i = 3 nums[3] = 3的情况
3 > 1，但此时Math.max(dp[i],dp[j]+1) = Math.max(2,2+1)此时还是dp[3] = 3

所以最后总结下来

1. 需要一个dp数组，默认全部填充1
2. 用双重循环填充dp数组，每次i位置的填充需要遍历nums[0,i-1]范围内的数据，同时比较dp[j] = Math.max(dp[i],dp[j]+1)

var lengthOfLIS = function(nums) {
    // 保存长度
    let n = nums.length;
    if(n == 0) return 0
    // 创建个对应长度的数组，并且都填充1,
    // 填充1是子数组最差也是包含自己，那么长度怎么都是1
    let dp = new Array(n).fill(1);
    // 需要返回的值
    let max = 0;
    // 遍历整个数组
    for(let i = 0;i < n;i++){
        // 遍历[0,i-1]范围的数
        for(let j = 0;j < i;j++){
            //如果成立nums[j] < nums[i]，那么这个数组就是递增的
            if(nums[j] < nums[i]){
                // 对比下之前的长度，和这次能够生成的长度
                dp[i] = Math.max(dp[i],dp[j]+1);
            }
        }
        max = Math.max(max,dp[i]);
    }
    return max;
};