学习笔记--数据结构与算法基础（青岛大学-王卓）--第六章图

视频链接:

数据结构与算法基础（青岛大学-王卓）–第六章图

本章知识框架:

1.图的定义和基本术语

• 图表示多对多关系
• 图是由顶点(V集合)和边(E集合)构成,G=(V,E)
• 无向图:每条边都是无方向的
• 有向图:每条边都是有方向的

上图G1的顶点V集合={V1,V2,V3,V4};E集合={V1->V3,V1->V2,V3->V4,V4->V5}
上图G2的顶点V集合={V1,V2,V3,V4};E集合={E1,E2,E3,E4,E5,E6,E7}

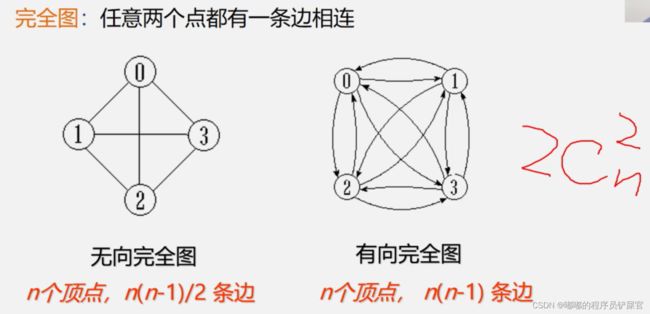
• 完全图:任意二个点都有一条边相连

• 稀疏图,稠密图,网,邻接,关联(依附)

弧:有向图中的边(为了区分有向图和无向图的边)

稀疏图(e表示边,n表示顶点的数目):

稠密图:
(e>=nlogn)

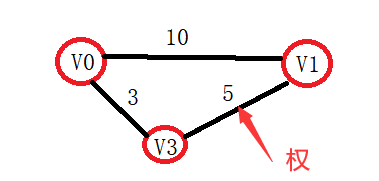
网:边/弧带权值

邻接：
(V1,V2)表示V1,V2互为邻接点

V1邻接到V2或V2邻接于V1

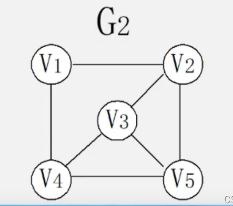
• 有向图和无向图的度

无向图V0的度为2(红色边的数量):

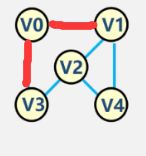
有向图V0的入度为1:

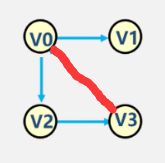
有向图V0的出度为2:

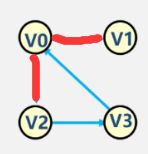
• 有向树:在有向图中仅有一个顶点的入度为0其余顶点的入度为1的图

• 路径,路径长度,回路(环),简单路径,简单回路(简单环)

• 连通图

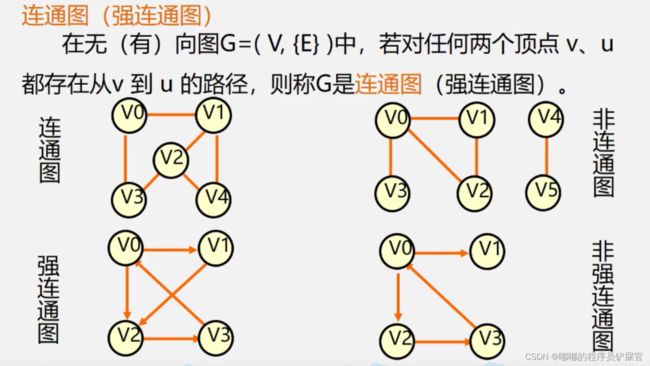
无向图的连通图:
下图连通图:V0可以去到任意顶点V1,V2,V3,V4,同理V1,V2,V3,V4也可以

下图非连通图:V0,V1,V2,V3无法去到V4,V5同理V4,V5无法去到V0~V3

有向图的连通图:
下图强连通图:V0可以去到任意顶点V1,V2,V3,同理V1,V2,V3也可以

下图非强连通图:V1无法去到V0,V2,V3

• 权与网

• 子图

• 无向图连通分量

G1,G2为G的连通子图并且都为极大连通子图(不管是G2或G1的顶点只要加入另外一个子图就会不在连通),G1,G2也称为G的连通分量

• 有向图强连通分量

下图是一个非强连通图(V1无法到达V0,V2,V3),将V1去掉看成一个子图,这时候V1和(V0,V2,V3)分别为G的强连通分量

• 极小连通子图,生成树,生成森林

极小连通子图:该子图是G的连通子图，在该子图中删除任何一条边子图不再连通

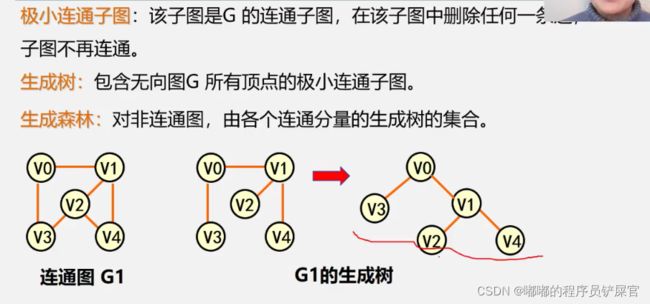
下图就是一个极小连通子图,删除任意一条边就不再连通

连通图G1的生成树:包含G1中所有顶点的极小连通子图

2.案例引入

• 六度空间理论
  
• 六度空间理论的验证
  

3.图的类型定义(抽象数据类型)

• 属性

• 操作

4.图的存储结构

• 顺序存储结构,图是没有顺序存储结构的,但是可以通过二维数组来表示元素之间的关系,这种方式称为数组表示法(邻接矩阵)
• 链式存储结构,链式存储结构的前驱和后驱不知道要定义多少(图是多对多关系)所以无法使用多重链表,但是可以通过邻接表,邻接多重表，十字链表来表示

数组表示法(邻接矩阵)

• 无向图的邻接矩阵表示法

• 有向图的邻接矩阵表示法
  
  

• 网(即有全图)的邻接矩阵表示法
  

• 邻接矩阵利与弊
  利:
  弊:
  
  邻接表表示法(链式)
  
  

• 无向图
  

• 有向图
  

邻接表(指针域指向出度方向接收顶点)
V1对应上图的V1->V3(数组下标为2),V1->V2(数组下标为1)

特点:

逆邻接表(指针域指向入度方向发出顶点)
V1对应上图的V4->V1(数组下标为3)

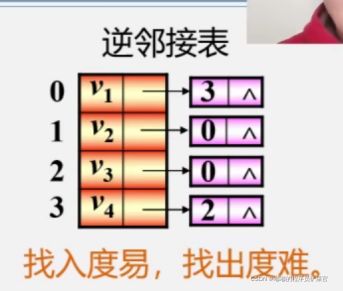
特点:

• 邻接表的特点

• 邻接矩阵与邻接表表示法的关系

• 邻接表中存在的问题

十字链表

• 什么是十字链表

• 十字链表结构

邻接多重表


上图V1指向V4和V2,(V1,V4)和(V1,V2)

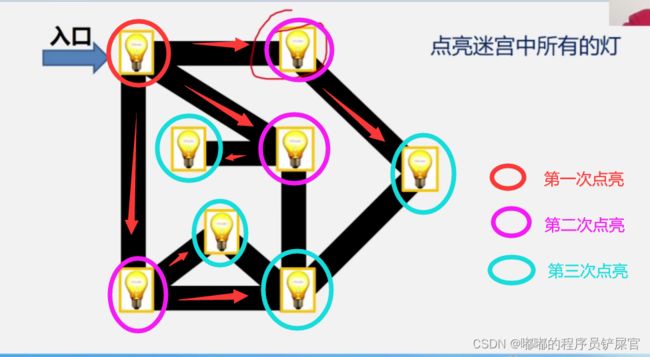
5.图的遍历

• 什么是图的遍历
  
  
  如何避免重复访问
  

• 图的遍历算法
  深度优先遍历(DFS)
  广度优先搜索( BFS)

深度优先遍历(DFS)

• 邻接矩阵表示的无向图深度遍历实现
  辅助数组用来避免重复访问
  
  

• 非连通图的遍历
  

• 深度优先遍历(DFS)效率分析
  
  广度优先搜索( BFS)
  
  

• 非连通图的广度遍历
  
• 实现(通过队列实现)
  
  
• BFS算法效率分析
  
• DFS并BFS算法效率比较
  

6.图的应用

最小生成树

• 什么是最小生成树

• 最小生成树的作用
  
• 构造最小生成树
  
• MST
  
• 构造最小生成树方法一: 普里姆(Prim)算法
  
• 构造最小生成树方法二:克鲁斯卡尔(Kruskal)算法。
  
• 两种算法比较
  

最短路径

• 最短路径
  

• 问题抽象

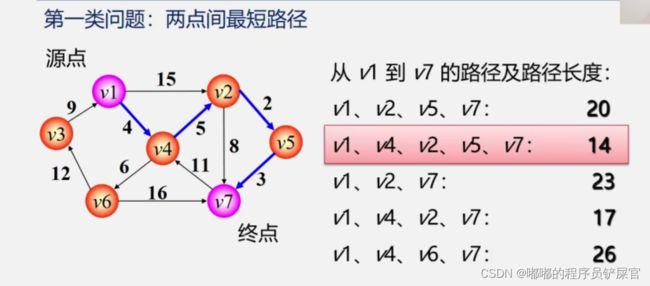
• 第一类问题:两点间最短路径

• 第二类问题某源点到其他各点最短路径
  
• 针对上述二个问题的算法

• 艾兹格.W:迪杰斯特拉(Edsger Wybe Dijkstra)
  
• Dijkstra算法

• 问题二的解决办法
  
• Floyd算法
  
  拓扑排序
• 有向无环图

• 有向无环图及其应用

• AOV网
  
  

• AOE网

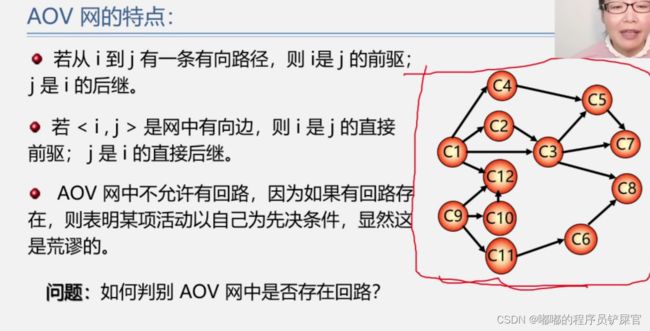
• 什么是拓扑排序

• 拓扑排序例子

• 拓扑排序的方法
  
• 拓扑排序的一一个重要应用
  

关键路径

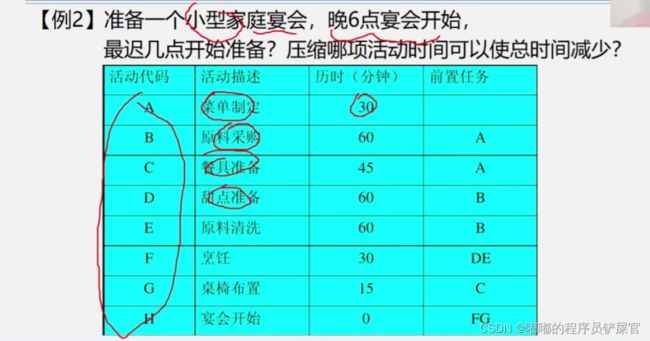
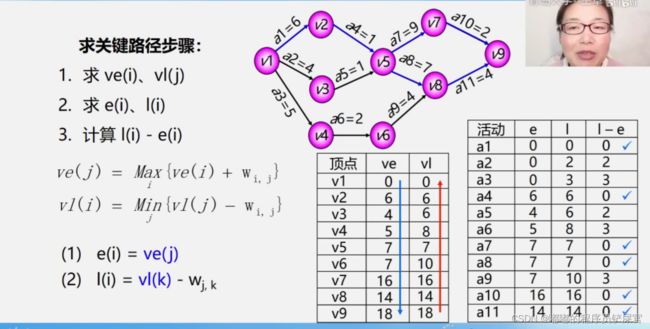
• 关键路径

• 对于AOE网,需要关心的二个问题

• 通过4个描述量确定关键路径