视觉检测设计与实践答题卡检测实验报告
一、实验目的
1、提取答题卡的信息
2、能够有效辨识答题卡的信息
二、实验内容
1、实验步骤
①配置python在实现图像处理下的运行环境,配置opencv-python,opencv-contrib-python,numpy库,这些库可以保证对于图像二值化的基本实现,在这些库的基础上,为了方便图像更加直观的可视化,又添加了matplotlib,wheel,pipllow库来实现数据的可视化。
②查阅资料,了解python编程语言下的opencv方法使用方式以及代码编写方法.
③根据实验要求,读取图像,生成灰度图,迭代阈值算法,计算阈值,图像二值化,显示处理结果
④找到连通域 v计算连通域的面积、中心、外接矩形 利用连通域提取答题框部分ROI
⑤hough直线提取,矩形框顶点定位
2、关键代码的设计、实现与执行
【报告要体现出设计思路】
【报告简要给出关键代码,注意,关键代码,关键代码,关键代码,禁止贴上代码原文或截屏】
【关键代码要具有可读性,可附上简单的说明或者程序流程图】
【可附上实验过程数据的截图,同时请注明截图内容】
【可以给出不同的实现版本,对比分析】
(1)图像二值化
首先将获得的图像进行灰度处理,可使用公式Gray=R0.299+G0.587+B*0.114,python+opencv库中可以直接调用cv2.cvtColor(image,cv2.COLOR_BGRA2GRAY)使图片转换为灰度图效果如下

原图 灰度图
转换为灰度图后有三种方式可以将其二值化:
①手动赋予全局阈值
ret, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
Cv2.threshold中第一个参数为目标灰度图,第二个为手动设置的阈值,第三个为最大值,最后一个为阈值类型,阈值常用类型有如下几种:
• cv2.THRESH_BINARY(黑白二值)
• cv2.THRESH_BINARY_INV(黑白二值反转)
• cv2.THRESH_TRUNC (得到的图像为多像素值)
手动设置全局阈值得到的效果图如上。
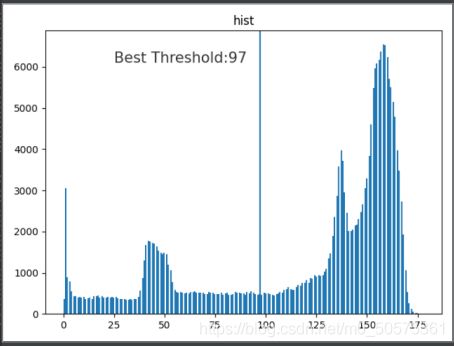
②迭代阈值分割算法
迭代阈值算法的流程图如下
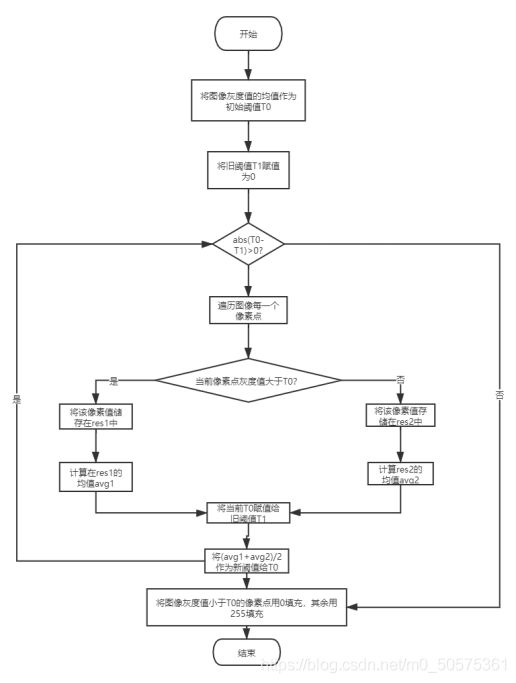
用代码描述则是首先读入图片并转化为矩阵,然后求出矩阵的大小,根据得到的矩阵求出初始阈值
zmin = np.min(im)
zmax = np.max(im)
t0 = int((zmin+zmax)/2)
使用迭代法计算最佳阈值
while abs(t0-t1)>0:
#遍历每一个像素点
for i in range(0,l-1):
for j in range(0,w-1):
#判断是否大于t0,分别存入两个数组res1和res2
if im[i,j]<t0:
res1=res1+im[i,j]
s1=s1+1
elif im[i,j]>t0:
res2=res2+im[i,j]
s2=s2+1
avg1=res1/s1
avg2=res2/s2
res1 = 0
res2 = 0
s1 = 0
s2 = 0
t1 = t0 #旧阈值储存在t1中
t0=int((avg1+avg2)/2) #计算新阈值
③自适应阈值分割
自适应阈值分割可以通过滤波器处理后二值化图片,也可以通过去除阴影,图像拉伸后二值化处理
滤波器处理可以在python+opencv下的
dst = cv2.adaptiveThreshold(src, maxval, thresh_type, type, Block Size, C)方法下进行
这个方法代表自适应阈值二值化
src: 输入图,只能输入单通道图像,通常来说为灰度图
dst: 输出图
maxval: 当像素值超过了阈值(或者小于阈值,根据type来决定),所赋予的值
thresh_type: 阈值的计算方法,包含以下2种类型:cv2.ADAPTIVE_THRESH_MEAN_C; cv2.ADAPTIVE_THRESH_GAUSSIAN_C.其中第一个代表均值像素计算
type:二值化操作的类型,与固定阈值函数相同,包含以下5种类型: cv2.THRESH_BINARY; cv2.THRESH_BINARY_INV; cv2.THRESH_TRUNC; cv2.THRESH_TOZERO;cv2.THRESH_TOZERO_INV.
Block Size: 图片中分块的大小
C :阈值计算方法中的常数项
效果图如下

第二种方法可以采用去除光照后灰度拉伸在采用迭代阈值分割算法进行二值化处理
去除光照可采用首先计算每个修改的像素块的大小然后使用高斯滤波进行处理
效果图如下

(2)连通域获取
首先求得图片内的最大连通域
Python+opencv下获取二值图连通域可使用skimage的measure.label
参数介绍:
label 是返回的已经将input中连通域标注为1,2,3。。num的标签数组
num 连通域个数
input_array 输入数组
neighbors 连通域计算样式
from skimage import measure
label, num = measure.label(input_array, neighbors=8, background=0, return_num=True)
获取最大连通域的方法如下
for i in range(1, num+1):
if np.sum(labeled_img == i) > max_num:
max_num = np.sum(labeled_img == i)
max_label = i
mcr = (labeled_img == max_label)
遍历所得的每一个连通域,从1开始是为了防止计算最大连通域时将外边框计算入内,每次遍历得到一个更大的连通域就将 max_label转为此连通域对应的下标,最后将连通域内下标为max_label的连通域赋给mcr
然后可通过
minr, minc, maxr, maxc = regionprops(labeled_img)[max_label-1].bbox
得到最大连通域的高度宽度,其中max_label-1的原因在于数组从0开始因此需要减去一才是应得的值,再通过crop函数裁剪就能得到连通域所对应的区域
region = img.crop((minc,minr,maxc,maxr))
矩形则通过matplotlib.patches所带的Rectangle可得到矩形边框
rect = mpatches.Rectangle((minc, minr), maxc - minc, maxr - minr,
fill=False, edgecolor='red', linewidth=2)
(3)harris角点检测
Harris角点检测的原理:
角点向任何方向移动变化都很大,Chris_Harris 和 Mike_Stephens 早在 1988 年的文章《A Combined Corner and Edge Detector》中就已经提出了焦点检测的方法,被称为 Harris 角点检测。他把这个简单的想法转换成了数学形式。将窗口向各个方向移动(u,v)然后计算所有差异的总和。表达式如下:
窗口函数可以是正常的矩形窗口也可以是对每一个像素给予不同权重的高斯窗口
角点检测中要使 E (µ, ν) 的值最大。这就是说必须使方程右侧的第二项的取值最大。对上面的等式进行泰勒级数展开然后再通过几步数学换算,我们得到下面的等式:
其中
这里 Ix 和 Iy 是图像在 x 和 y 方向的导数。(可以使用函数 cv2.Sobel()计算得到)。
然后就是主要部分了。他们根据一个用来判定窗口内是否包含角点的等式进行打分。
其中
λ1 和 λ2 是矩阵 M 的特征值
所以根据这些特征中我们可以判断一个区域是否是角点,边界或者是平面。
当 λ1 和 λ2 都小时,|R| 也小,这个区域就是一个平坦区域。
当 λ1≫ λ2 或者 λ1≪ λ2,时 R 小于 0,这个区域是边缘
当 λ1 和 λ2 都很大,并且 λ1~λ2 中的时,R 也很大,(λ1 和 λ2 中的最 小值都大于阈值)说明这个区域是角点。
可用下图表示我们的结论
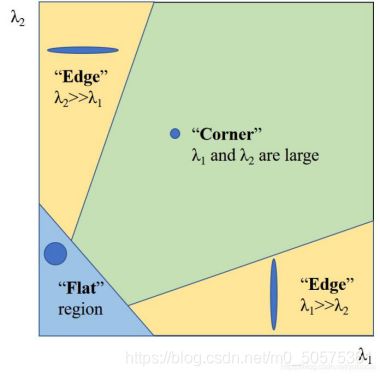
所以 Harris 角点检测的结果是一个由角点分数构成的灰度图像。选取适当的阈值对结果图像进行二值化我们就检测到了图像中的角点。
Harris角点检测函数
cv2.cornerHarris(src, blockSize, ksize, k, dst, borderType)
src:数据类型为float32的输入图像
blockSize:角点检测中要考虑的领域大小
ksize:Sobel求导中使用的窗口大小
k:Harris 角点检测方程中的自由参数,取值参数为 [0,04,0.06].
dst:目标图像
borderType:边界类型
gray = np.float32(gray)
输入图像必须是 float32,最后一个参数在 0.04 到 0.05 之间
dst = cv2.cornerHarris(gray, 2, 3, 0.04)
#进行膨胀操作
dst = cv2.dilate(dst, None)
#将满足条件的角点用红色标注出来
img[dst > 0.005 * dst.max()] = [255, 0, 0]
(4)hough变换
Hough变换思想(参数空间变换):
在原始图像坐标系下的一个点对应了参数坐标系中的一条直线,同样参数坐标系的一条直线对应了原始坐标系下的一个点,然后,原始坐标系下呈现直线的所有点,它们的斜率和截距是相同的,所以它们在参数坐标系下对应于同一个点。这样在将原始坐标系下的各个点投影到参数坐标系下之后,看参数坐标系下有没有聚集点,这样的聚集点就对应了原始坐标系下的直线。
在实际应用中,y=kx+b形式的直线方程没有办法表示x=c形式的直线(这时候,直线的斜率为无穷大)。所以实际应用中,是采用参数方程p=xcos(theta)+y*sin(theta)。这样,图像平面上的一个点就对应到参数p—theta平面上的一条曲线上,其它的还是一样。
Hough变换思想(参数空间划分网格统计):
为了检测出直角坐标X-Y中由点所构成的直线,可以将极坐标a-p量化成许多小格。根据直角坐标中每个点的坐标(x,y),在a = 0-180°内以小格的步长计算各个p值,所得值落在某个小格内,便使该小格的累加记数器加1。当直角坐标中全部的点都变换后,对小格进行检验,计数值最大的小格,其(a,p)值对应于直角坐标中所求直线。
Python+opencv所用函数
HoughLinesP(image, rho, theta, threshold, lines=None, minLineLength=None, maxLineGap=None)
image: 必须是二值图像,推荐使用canny边缘检测的结果图像;
rho: 线段以像素为单位的距离精度,double类型的,推荐用1.0
theta: 线段以弧度为单位的角度精度,推荐用numpy.pi/180
threshod: 累加平面的阈值参数,int类型,超过设定阈值才被检测出线段,值越大,基本上意味着检出的线段越长,检出的线段个数越少。根据情况推荐先用100试试
lines:这个参数的意义未知,发现不同的lines对结果没影响,但是不要忽略了它的存在
minLineLength:线段以像素为单位的最小长度,根据应用场景设置
maxLineGap:同一方向上两条线段判定为一条线段的最大允许间隔(断裂),超过了设定值,则把两条线段当成一条线段,值越大,允许线段上的断裂越大,越有可能检出潜在的直线段
lines = cv2.HoughLinesP(edges,1,np.pi/180,180,minLineLength=60,maxLineGap=10)
lines1 = lines[:,0,:]#提取为二维
for x1,y1,x2,y2 in lines1[:]:
cv2.line(img,(x1,y1),(x2,y2),(255,0,0),2)
参数设置为180时得到的图像最合理
3、实验结果分析
【测试数据说明,实验结果的正确性分析,程序不足点分析等】
第一部分(图像二值化)
图像二值化部分,总共采用了三种方法对图像二值化进行处理,分为手动设置全局阈值,局部自适应阈值(均值滤波分割和去除阴影),在阴影影响较为严重时,去除阴影图像拉伸的方法更加适用,而在阴影影响很小的情况下,均值滤波分割对信息的还原度最高
分别为去除阴影后采用迭代阈值分割法和均值滤波分割
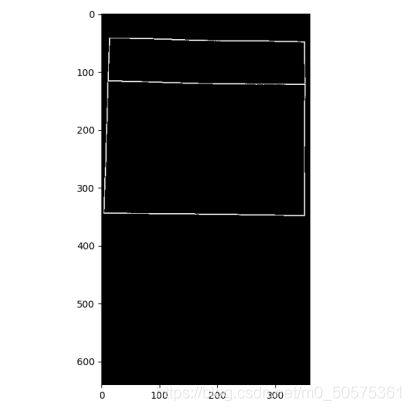
第二部分(连通域)
连通域可以识别计算出最大连通域及他所对应的矩形边框的坐标
①
②
第三部分(harris角点检测)
基本能检测出关键点,同时调整参数的话会使点的数量发生改变
第四部分(hough变换)
基本能测绘出所需要的线段
三、实验思考
Python+opencv为我们封装了大量与视觉检测有关的方法,熟练使用这些方法我们就可以用很少的代码量实现复杂的功能,但同时,我们在使用这些方法的时候也需要了解这些方法背后的原理和其他的一些实现方法,在面对需要更加复杂具体的功能时,我们需要自己的算法加入其中才能完成更加充实可靠的功能。
(还请各位尽量多加自己的东西。切勿照搬)