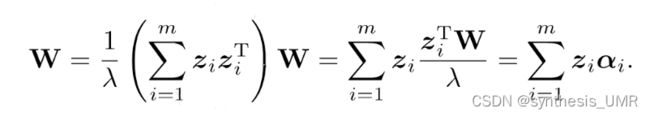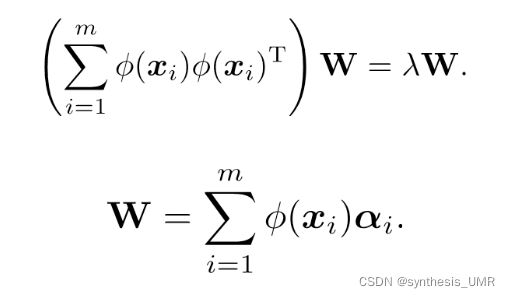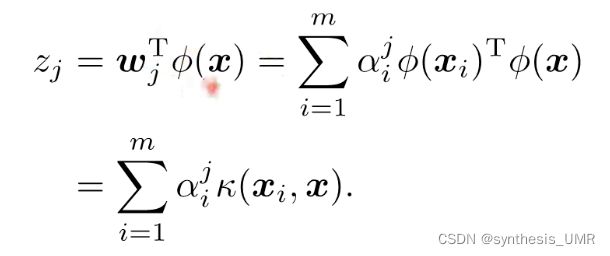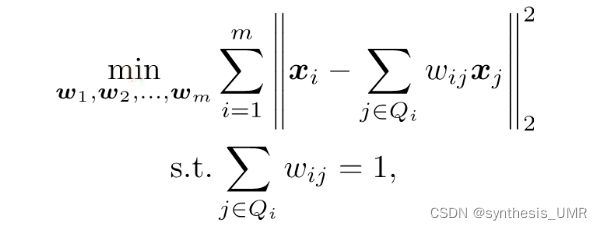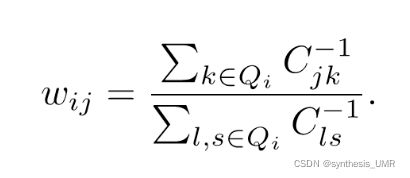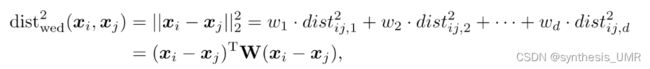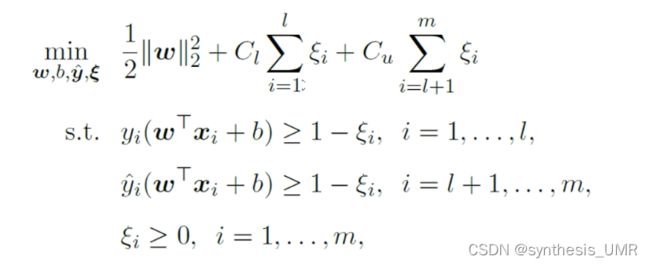模式识别机器学习PRML考前自测
绪论
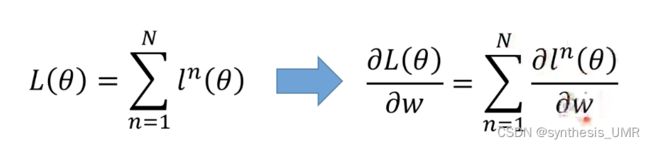
1、请介绍一下机器学习的整体框架
机器学习和模式识别基本一个东西,模式识别是工业界的称呼而已。机器学习是人工智能下属的子领域,用来辅助在大数据时代进行数据分析与数据管理,应用于数据挖掘工作。人工智能的其他子领域包括比如NLP CV等领域。
机器学习根据是否有监督可以分为:全监督学习(比如naive bayes、回归、SVM),无监督学习(聚类、降维),半监督学习 按照是否应用了神经网络可以分为:传统机器学习和神经网络(如果使用了深度神经网络,那么为深度学习)
2、介绍一下机器学习的历史吧
56-60 数学家主要在进行自动定理证明系统的研究
70-80 创造出了各种专家系统,将知识交给系统
90s到现在 让机器自己学习
3、机器学习和大数据有什么关系?
大数据时代,我们收集、传输、存储数据,通过机器学习 云计算 众包分析数据,将其转化成有用的信息供我们使用。
(机器学习帮助我们分析数据)
4、机器学习的基本术语,请用自己的语言表述
监督学习:有标签
无监督学习:没标签
数据集、训练、测试:train set 和 test set,包含特征信息和如果有的话 标签
示例、样本:数据集中的每条记录
样例:?带标签的记录?
属性、特征:描述样本的信息单元
属性值:mp hp
属性空间、样本空间、输入空间:属性 样本张成的空间
特征向量:映射组合成向量模式方便处理
标记空间、输出空间:输出的是映射到语义空间后的分类结果也好,判断也好 标记1001010011
假设、真相、学习器:对于模型而言的
分类、回归、二分类、多分类、正例负例、独立同分布、泛化:字面意思
5、机器学习的基本过程是什么呢?
首先进行表示:将数据进行特征化表示,通过向量表示法
然后进行训练,给定数据样本集从中学习出规律模型,找出最优的拟合函数
最后进行测试:对于新的数据样本利用学到的模型进行预测
6、No free lunch therom
不存在哪个模型和算法是完美的
前提:所有问题出现的机会相同,所有问题同等重要
7、既然没有完美模型,模型如何进行选择和评估?
主要原则:要找到泛化能力强的学习器
想要拟定一个评价标准,首先我们要衡量误差的大小
7.1 误差有哪几种类型呢?
训练误差(经验误差)、测试误差
泛化误差:除了训练以外的所有样本
经验误差不能过小,否则会过拟合;也不能太大,否则会欠拟合
我们现在有了误差的定义,相当于发明了阿拉伯数字,我们的最终目的是选择出好的模型,那么很自然地提出三个问题:怎么获得测试结果?怎么度量性能?怎么判断差别?
7.2 评估的方法3种
现在我们手上有数据、模型,可以求得误差。但是数据怎么划分就是评估的关键。
原则:测试集和训练集应该互斥才行,要不然作弊了
常用:留出法 交叉验证法 自助法
7.2.1 留出法
留出法将数据集拆分成测试集和训练集(互补)通常比例在2:1到4:1
7.2.2 k折交叉验证
数据分成k个大小相似的互斥子集,每次用k-1个子集的并集作为训练集,剩下1个当测试集,最终返回k个测试结果的均值。k最常用10
随机划分p次进行上面的操作叫做p次k折交叉验证
如果k==数据中样本大小,称留一法
7.2.3 自助法
对数据做m次有放回采样,D/D’作为测试集
约有1/3样本没在训练集中出现,对于集成学习帮助很大,在数据集小,难以有效划分训练集、测试集的时候很有用。但是导入了估计偏差,所以数据量够的时候还是用留出法
一个模型,即使算法相同,但是里面有很多的参数的不同也将导致最终答案不同效果不同
7.2.4 参数调整
算法人工设定的参数:超参数
模型参数:一般由学习确定
先产生若干模型,然后基于某种评估方法进行选择参数
要知道训练集 测试集和验证集之间的区别:参数选定后需要用训练集+验证集重新训练模型
模型最终的参数确定了,如何划分测试数据也确定了,下面可以进行训练了。但训练完后我们还得分析数据...
7.3 如何评估性能优劣?性能度量
性能度量用来反映泛化误差,衡量标准不同产生的结果不同(比如回归问题一般用均方误差
7.3.1 对于分类任务我们用什么?
我们使用错误率和精度来进行衡量
错误率是我分类分错了的占总体比重
精度是分对了的占总体的比重
7.3.2 介绍一下混淆矩阵和查准率与查全率吧
TP(真正例)TN(真反例) FP(假正例)FN(假反例)
后面一个字母表示我把它分到了什么类,前面一个字母代表我分对了没
查准率:意思是我认为是对的这些里面有多少是真的对的
P=TP/(TP+FP)
查全率:意思是在所有真的正确的当中我查出了多少
R=TP/(TP+FN)
PR是此消彼长的
7.3.3 有了查全率与查准率,我们可以用什么模型?更常用的是什么模型?
P-R曲线,BEP点 曲线无法区分的时候可以使用BEP
Fscore更常用 F1= 2PR/P+R
Fb=(1+b^2)PR/(b^2*P)+R b>1偏向于查全 b<1偏向于查准
还有额外的一个AUC ROC模型
横纵轴是tpr和fpr表示 真正正例中分对的 和 真正负例中但是被错分成负例的的 他俩是一起增减的
7.3.4 对于不同模型训练出来的数据,如果采取相同的评估方法在相应度量下比大小,结论严谨吗?
不可以。
因为测试性能不等于泛化性能,测试性能随着测试集变化而变化,且大多数机器学习算法本身具有一定随机性。所以需要第三步:假设检验。从统计学的意义上推断出A的性能是否优于B以及这个结论的把握有多大。
现在我们已经了解了如何划分数据以及如何度量模型的好坏,我们来研究一下更加抽象的问题:误差究竟是哪儿来的?人为什么能分对的机器分不对?
7.4 偏差-方差分解
对于回归任务,泛化误差可以拆解为bias var 和常数epsilon
bias是指期望输出和真实输出之间的差别 学习能力
var是指同样大小的训练集的变动导致的性能变化 数据充分性
epsilon是当前任务任何学习算法所能达到的期望泛化误差下限 学习任务本身的难度
偏差和方差通常存在冲突
训练少时偏差大,训练大时方差大
以上是机器学习绪论部分,主要向我们阐述了1、什么是机器学习以及 2、如何去对模型,对数据进行处理,得到最适合的模型。但是还没有教我们模型是什么,以及如何表达特征,所以从下一章开始我们就要正式学习这两者进行实践了。每个模型要把握住他的作用、思想和他的优缺点所在(和如何改进),接着对其数学原理要非常熟悉考试才能ok。但在开始模型之前,我们还得对特征的提取方法更加熟悉一些。表达、训练、测试三步走,表达也是很重要的。所以我们下面将介绍两个cv领域的特征子,熟悉线性滤波,尺度变换,核函数,梯度直方图等多种数学工具。从而对机器学习的第一步:表达 有更加深刻的理解。
01 HOG特征
histogram of gradient
1、总结HOG作用、思想、优缺点
作用:提取局部特征边缘、形状的特征描述子
思想:图像存在边缘,对应灰度图一定有较大梯度。其本质是梯度的统计信息来作为特征
擅长:几何和光学转化不变性,色彩影响较小,可描述局部形状
不擅长:尺寸大的图形(通过PHOG解决,把一串HOG连起来)速度慢,不能实时,遮挡问题,噪点敏感
2、数学预备知识
自行默写离散情况下x y方向梯度表达式,梯度强度 梯度方向 sobel算子 卷积核线性滤波(卷积进行180翻转,协相关不需要)
3、具体步骤
现在手上有一幅图,比较大,所以我们先要进行窗口移动算法
(1)窗口移动
选取出我们需要检测的位置
好了,窗口得到了,下一步我们需要对图像进行处理。主要是为了减少光照影响
(2)Gamma校正
调节图像对比度,减少图像的光照不均和局部阴影,对于即将过曝或曝光不足的照片进行矫正
ok图像变成灰度图了,下面可以开始计算梯度了
(3)计算图像梯度
梯度图移除非显著信息,加强了显著特征。水平垂直方向使用的是Sobel算子
要会计算一个像素的梯度值和梯度方向哦
现在我们获得了两张表:一张表示梯度值,一张表是梯度方向。然后我们把它们化成直方图。那么就需要横轴和纵轴。怎么画?
(4)以Cell为单位计算梯度直方图
我们窗口还是太大,还可以继续缩小成8*8的小格,称为一个cell
180分成9个栏,每个20度,看梯度值和对应梯度方向,属于哪个该栏就加该梯度值,于是就得到了直方图啦
这样可以减少计算量,对于光照等环境也更加鲁棒
好滴,那么现在直方图也有了,我们可以进一步进行归一化来彻底让描述子独立于光照的变化
(5)以block为单位进行归一化
窗口 cell block,block居于两者中间16*16 4个cell
归一化的方法是让向量的每一个值除以向量的模长
数据处理完毕,我们看看得到了什么?
(6)组合成HOG特征向量
每个block 16*16 ,分成4快8*8, 每个8*8中都进行了梯度直方计算,分了9栏。所以一个block里有4*9 36个特征。再乘以block的数量就可以得到最后的特征总数啦~
我们得到了一维特征向量*1,接下来我们用训练好的分类器,将该一维特征向量输入后就得到了我们所要识别和检测的内容的分类信息了。是不是很简单呢?
WGG CBH
02 SIFT特征
scale of invariant feature transform 尺度不变特征变换
我们想要拍全景照片,那么只要在不同位置拍摄出的照片找出对应的相同点然后合成一下就完事儿了。但是不同时间不同光照不同位置的像对应起来,传统算法经常提取角点或边缘,对于环境的适应能能力差。所以需要一种能够适应上述情况的目标识别方法。
1、SIFT的作用、思想、优缺点
作用:将一幅图像映射成一个局部特征向量集
思想:将图像变换成一个局部特征向量集,本质是在不同尺度空间上查找特征点(关键点)并计算出关键点方向的问题。
优点:具有平移、缩放、旋转不变性,同时对于光照变化,仿射投影也有一定不变性。辨别力强,多量,可扩展性(与其他特征向量联用)。
缺点:实时性差,特征点不足 PCASIFT降维主成分分析 CSIFT彩色尺度特征不变 SURF超快 ASIFT等
2、具体步骤
我们上面说了,只要找到特征点把他描述出来,然后再匹配一下就ok了。那首先我们来研究怎么检测出来特征点:
尺度空间就是如果给你一棵树,那就忽略细节观察宏观;如果给你树叶,那就关注细节观察微观。这样就可以得到不同尺度空间下的序列啦。
构建尺度空间采用高斯核函数,因为他是唯一尺度不变的核函数,而且可以获得多组多层图像,他还是线性的。尺度空间图像生成的就是当前图像和不同的核函数参数卷积运算后获得的图像。
尺度空间有层和组之分,层间最低一幅图是通过隔点采样获得的图像,一层里有很多组。
(1) 构建尺度空间
构建高斯金字塔 对图像做高斯平滑和降采样,加上高斯滤波保证连续性。产生多组图像
欠采样时进行低通滤波处理,保证不出现高频虚假信息;减小图像尺寸时使用高斯模糊
高斯差分:是对于组间的图两层相减获得的,所以像素值的变化越大说明他是轮廓
ok,现在我们获得了一个很反常识的尺度空间,它里面有很多层,层间是通过上一层降采样获得的。每一层有很多组,组间是通过高斯模糊得到的。
![]()
接下来我们要寻找特征点,从而确定我们要找的点。一个像素要和自己周边的8个和上下2*9个26个点进行比较,确定在尺度空间和二维空间中都是极值点。
(2)特征点定位
关键点是由DOG空间的局部极值点组成的。
嘛这样说确实很不精确,特征点在三位尺度空间的局部极值点,xy是整数像素,delta是离散尺度,需要DoG空间拟合进行精确定位。
DoG核函数可以近似为LoG函数,LoG定义为原始图像I与一个可变尺度的2维高斯函数G的卷积运算![]()
特征点精确定位推导自己推一遍~(泰勒展开求偏导得到偏移量然后取极值点)
如果偏移量在任何分量上的取值大于0.5,说明精确极值点更接近邻近点,换邻近点重复上述流程
还需要去除不稳定的特征点
这样就可以在不同的视角,光照,旋转,尺度变化下得到相同的特征点啦。然后我们需要确定特征点的主方向。因为光光找到点还不行,照片旋转了的话怎么才能将他们重叠呢?如果特征点有一个方向信息就好了。
(3)特征点主方向确定
尺度不变性:尺度空间求得的极值
方向不变性:将圆周分为36份,计算特征点附近的像素梯度和幅值,根据每个像素幅值和距离中心的高斯距离绘制梯度直方图,将直方图中最大方向作为特征点主方向(如果有其他值达到80%),则指定为辅方向)
OK,图像的关键点检测完毕了,每个关键点有位置、尺度、方向三个信息,这样就保证了关键点就算平移,旋转,缩放也不会发生变化。
然后我们要用向量来记录这些点。是不是只记录一下特征点就行呢?还可以做得更好。我们可以把对于特征点有贡献的像素也记录下来,让特征点具有更多的特性:光照变化,视角变化等。那么怎么才能认为这个点是有贡献的呢?我们可以对特征点周围图像区域分块,计算块内的HOG。
(4)特征描述
首先确定描述子的窗口大小,坐标轴旋转,x正方向和主方向重合
旋转角度后新坐标公式,默一下(叉乘)
然后计算窗口内每个像素梯度幅值和方向
将窗口划分成4*4子区域
计算每个子区域梯度幅值直方图 8bins 一栏45度
得到4*4*8=128维向量描述子 这128维的向量就叫做SIFT特征向量
好了,特征向量终于求出来了,我们的每个特征向量里有旋转正方向后的128维HOG数据。那么经过尺度变化后的各个图的特征向量信息是一摸一样,直接可以相等的吗?当然不是。所以我们还要进行匹配处理
(5)特征匹配
可以在特征空间通过特征描述子之间的距离判断匹配程度,可以使用kd树来进行欧式距离采样。
这样我们在不同尺度空间下获得的不同特征点就一一对应起来啦,后面还要进行旋转啊什么的操作就留给你假期去实现了!加油加油
两个特征描述子讲完了,我们发现一般就是有一个很浅显的原理或者想法,然后科学家想了些办法对数据进行了处理,得出了具有各种好性质(不变性)的特征向量。可以非常好地反映图像的信息(一般就是轮廓信息)。这就是机器学习的第一步:表示。然后下一步是进行模型训练,我们可以归纳出各种模型,将特征向量输入来解决各种问题。
03 线性模型
线性回归
选择函数的步骤3步:决定一组函数,评定函数的好坏,选出最好的函数
1、线性回归的作用、思想,优缺点
作用:回归预测模型
思想:画线。。。使均方误差最小
优点:形式简单,容易建模,可解释性好 是非线性模型的基础
缺点:噪音敏感 鲁棒回归 随机取样一致 RANSAC
2、一元线性推导
1、回归问题嘛,先评定均方误差
2、要二元函数最小,对w b求导 =0
3、解的闭式解,说明直接代入就行
3、多元线性回归推导
1、写出一般形式(向量形式)fx=wx+b 最终就是要解出w b
2、对系数、未知数进行矩阵化,写出矩阵形式的最小二乘法公式。然后求导
3、满秩矩阵下,可以直接写出闭式解
4、非满秩,归纳偏好选择解or引入正则化对解空间做限制
线性是对参数空间的线性,比如参数空间里面有一个x3,如果x3是由y^3得来的,并不影响参数空间的线性。也就是所谓的核学习方法
4、对数线性回归公式
即输出标记的对数是线性模型逼近的目标
1、写出广义线性模型和联系函数(单调可微函数)
如果要我们做一个预测问题,我们很自然地就会采集所有影响因素x的信息并得到最终的结果y,然后通过多元线性回归去预测新输入样本的结果。但是如果我们想要的结果是判断是or不是,怎么办呢?此时我们就需要引入新的方法和映射
我们输入wX,如果偏左的都是小于0,偏右的都是大于0,那么就可以做判断了。什么函数有这种特性?log函数。logy=wX看起来很不错。解决了显著性问题。要是能对称就更好了
引入几率解决这个问题,这样我们输入的wX就将对应获得一个几率。然后我们再设定阈值让大于0.5判断为是,经过三次映射,终于可以确定最终的分类啦。这就是logistic回归的思想
但是这是正向推导,我们还要反向求解w才行。就像一元线性回归我们将与均方差的距离差定义为损失函数一样,我们也要先定义一个损失函数。直观地想,当分类真实情况是1时,如果我们求出的p趋近于0,那就不太好。可以用下图描述
−logpi
![]()
反过来也是一样的。然后构建一个整体损失函数:
Cost=i=1∑m[−yilog(1+eθXeθX)−(1−yi)log(1−1+eθXeθX)] 这个就是对数似然函数了
然后极大似然估计做一手就可以解出θ也就是我们要求的w了
Logistic回归
1、作用、思想、优缺点
作用:二分类问题
思想:用回归模型完成二分类任务,线性回归不是会输入一个x得到一个y吗?我们比如训练一个单位阶跃函数,那就可以帮我们进行判断啦
优点:无需事先假设数据分布,可以得到类别的近似概率预测,可以直接应用在现有的数值优化算法中求最优
缺点:单位阶跃不连续,使用sigmoid函数族(对数几率函数)
2、推导
1、写出对数几率函数
2、对数几率:样本作为正例的相对可能性的对数 这是难点,反直觉的地方
3、然后使用极大似然估计和梯度下降、牛顿法进行求解(这部分不要看了,凸优化技巧不够)
线性判别分析LDA
linear discrimination analysis
1、作用、思想、优缺点
作用:二分类判别分析,是一种监督降维技术
思想:将空间中的点映射到一条直线上,使同类型的点尽可能近,不同类型中心距离尽可能大
用数学语言来说就是让同类样例投影点的协方差尽可能小,类中心之间的距离尽可能大
优点:
不足:
2、推导
1、写出最大化的目标
2、类内散度 类间散度 广义瑞利商
3、拉格朗日乘子法(等式约束)
4、奇异值分解
LDA贝叶斯决策论解释:LDA最优分类的情况
3、推广:多分类LDA
监督降维技术,将样本投影到N-1维空间,也是通过更新全局和类内的散度矩阵获得解答
多分类学习
将二分类推广,把问题拆成小问题,给每个二分类问题训练一个分类器。对于每个分类器的预测结果集成,从而获得最终的多分类结果。
1、拆分策略有哪些?
一对一 一对其他 多对多
2、介绍一下一对一吧OvO
我们将N个类别进行两两配对,N(N-1)/2个二分类任务 N(N-1)/2个二分类器
测试阶段:产生N(N-1)/2个二分类结果,最后投票预测最多的就是最终类别啦
3、一对其他呢?OvR
一个正类,其他的都是负类,然后用分类器分类,置信度最大类别作为最终类别
4、他们两个的性能指标怎么样?
在多数情况下预测两者差不多
5、介绍一下多对多
若干个正类,若干个负类,纠错输出码
思想:划分M次获得M个任务,测试样本也交给M个分类器,获得的编码预测。然后距离最小的类别就是我们的最终类别了。
ECOC编码 编码长、纠错强
类别不平衡问题
不同类别训练样例数差距很大(正类为小类)的时候,训练出来的模型往往不好
要想正反例平衡,我们可以再缩放操作
1、再缩放包含什么操作?
欠采样:去除一些反例让数目接近 集成学习
过采样:增加一些正例GAN
阈值移动
线性模型总结
1、在各个任务下各个模型优化的目标总结
最小二乘法:为了最小化均方误差
对数几率回归:是为了最大化样本分布似然
线性判别分析:投影空间内可以最小化类内散度,最大化类间散度
2、参数的优化方法
最小二乘法:线性代数
对数几率回归:凸优化下降法,牛顿法
线性判别分析:矩阵论、广义瑞利商
后两者涉及到的知识不够熟悉,必须要进行细化才行。
累死,机器学习并不是这么好弄得,小小一章线性模型能考的东西比概统还多(今天你辱概了吗~)但是我们也发现了,映射和抽象是机器学习模型学习的中心,数理优化是机器学习的最常用方法。那是不是所有模型都是整这种数学优化的活儿呢?也不完全是。接下来我们来学习决策树
04 决策树
假设我们要预测今天去不去打球,下雨的话我不去,下小雨温度高的话我去,晴天挂大风我不去balabala,我们可以把它组合成一个树状结构,从根走到叶子节点就可以判断了。这样我们并不需要把数据映射成数据处理。但最大的问题在于我们怎么构建决策树?怎么选择根节点,怎么选后继,什么时候停止?
1、思想、作用,优缺点
思想:模拟人的二分思考方式得到结论
作用:二分类问题
优点:列出了全部可行方案和各种状态,直观显示整个决策问题在时间和决策顺序上不同阶段的决策过程。
缺点:使用范围有限,有些模糊的不能用数量表示的决策不方便用
2、决策树怎么进行划分呢?
纯度:目标变量的混乱程度
我们希望随着划分的进行,数据的纯度越来越高,这样分支就会少。
3、划分的经典方法能阐述一下吗?
信息增益方法 增益率 基尼指数
引入系统论中的信息熵:表示信息的不确定度,是度量样本集合纯度的最常用指标之一
信息熵公式默一下 信息熵越高,纯度越低
接下来我们就可以计算使用属性a对样本D进行划分所获得的信息增益了:
信息增益公式默一下
父节点的信息熵减去所有子节点的 归一化信息熵
选择信息增益最大的作为节点(计算题算一下)
4、信息增益方法有什么问题呢?
信息增益对可取值数目越多的属性有偏好,但是他们的泛化性能可能并不好
所以我们可以引入增益率:默一下
可取数目越大,增益率越小。所以增益率准则对于可取值数目较少的属性有偏好
为了解决这个问题引入启发式:
先找出信息增益高于平均水平的属性,再找出增益率最高的
5、基尼指数怎么作为纯度的度量?
基尼值反映了从D中随机抽出两个样本,其类别标记不一致的概率
基尼值越小,纯度越高
应当选择使划分后基尼指数最小的属性作为最优划分属性
好滴,划分构建决策树的方法我们学到了,但是有一个严重的问题:样本中不是所有的属性都有效果的,有些会起反效果导致过拟合情况的出现。所以对于决策树我们需要学习剪枝来对付过拟合。线性回归就没这问题因为求最小误差并没有让预测值和经验集一摸一样。但是决策树因为是二值判断,把构建用的数据输入基本一定会输出正确答案滴。
怎么才能提升泛化能力,避免过拟合呢?还记得我们学的训练集和验证集吗?我们可以用验证集来判断某个节点的划分能不能带来决策树泛化性能的提升。
6、阐述预剪枝的过程
在生成过程中,对每个节点在划分前进行估计。如果不能带来泛化性能的提升那么就停止划分并将当前节点作为叶节点,类别标记为训练样例数最多的类别。
例题做一下
优点:降低过拟合风险,减少时间开销
缺点:欠拟合风险
7、阐述后剪枝的过程
一颗完整的决策树,自底向上对非叶子节点考察,如果该节点对应子树替换成叶子可以带来泛化性能提升,那么就将该子树替换成子结点
例题做一下
优点:欠拟合风险小,泛化性能往往好于预剪枝决策树
缺点:训练时间开销大,训练完了完整树还得训练
我们上面讨论的全都是离散的属性,但是有时候也有连续属性需要分类,比如西瓜的颜色是离散的,但西瓜的含糖量,密度等信息是连续值,此时怎么处理呢?
8、连续信息处理
连续属性离散化(二分法)
首先将出现的n个连续属性递增排列,考虑n-1个候选划分方式(两两数据之间的中点)
然后采用离散属性值方法,选取最优的划分点
计算信息增益选择信息增益最大的划分点,这样就确定了连续属性的划分点
如果当前结点划分属性为连续属性,该属性还可以作为其后代结点的划分属性。这个和离散属性不同
然后我们来考虑些实际问题:如果样本的属性出现缺失的时候,我们应该怎么处理呢?如果不用的话还挺浪费的。如果要使用的话就要解决属性缺失下如何进行划分属性选择?或者给定划分属性,如果样本在此属性上的值缺失的话,如何对样本进行划分?
9、缺失值处理
如何在属性缺失的情况下进行划分属性选择?
我们可以定义无缺失值所占比例,无缺失值样本中第k类所占比例,和无缺失值样本中在属性a上取值a^v的样本所占比例(反正就是把缺的给丢了,关注可以用的那些数据)
p,pk,rv
这样的话我们就可以求解出缺失信息的香农熵,从而进行选择
如果给定划分属性,若样本在该属性上的值缺失,那么如何对样本进行划分?
如果取值已知,则将x划入与其取值对应的子节点,且样本权值在子结点中保持为wx
如果取值未知,则将x同时划分入所有子节点,及那个样本权值在和属性值av对应的子结点中调整
(同一样本以不同概率划分入不同的子结点中)
例题做一下哈
以上的称为单变量决策树。但是我们知道现实中,很多东西需要多个变量结合才能合理进行分辨。比如说我们单单通过西瓜的密度和含糖量进行判断,虽然能得到结果但是不如通过密度*0.6+含糖量*1.1来判断(举例而已)。这种判断条件的变化就是多变量和单变量的区别。这时候复杂度就会发生极其恐怖的递增,先了解为主。
OK,决策树搞定了。这个比线性模型简单吧,只要不断重复计算香农熵挑出信息增益最大的选作划分结点的条件就可以了。还要掌握连续和缺失时的划分条件。本着一个容易一个难的原则,接下来,SVM闪亮登场kira~!
05 支持向量机SVM
support vector machines
1、SVM作用、思想、优缺点
思想:找到一个超平面,使支持向量到超平面的距离最大从而最为显著地划分类别
作用:二分类任务
优点:大部分训练样本点没有用,直接用支持向量就行了
不足:SVM永不为奴!
根据思想,我们要定义距离的意义并且在数据集中确定支持向量。
2、怎么定义距离?
点到超平面的远近可以反映分类预测的确信程度
而符号可以表示分类的正确与否
y(wx+b)可以表示分类的正确性和确信度 分对了为正 分错了为负,模值可以反映远近(确信度)
所以我们引进函数间隔和几何间隔:函数间隔是各个点计算出最小的y(wx+b)(对应的点就是支持向量)
几何间隔是除以w的模后得到的点到平面的距离
好滴,距离定义好了我们要让超平面离两类数据之间最远,这是一个凸二次规划问题,约束式是不等式所以使用KKT条件。对于SVM,我们输入线性可分的训练数据集,输出最间隔分离超平面和分类决策函数。线性可分情况下支持向量是数据集中与分离超平面距离最近的样本点。是让约束条件等号成立的点。H1:wx+b=1和H2:wx+b=-1称H1,H2是间隔边界。
硬间隔最大化
使用对偶理论可以将我们要求解的凸二次规划问题变成其对偶问题,使用KKT和反证法证明。
证明的话,自己证一遍?
SMO Sequential minimal optimization
1、引入拉格朗日乘子 原始问题对偶成 maxa minwb L(w,b,a)
2、对wb求偏导为0,求出 minwb L(W,B,A)
3、然后求解上式的mina ,就可以得到最优解a
4、w和a之间有关系,a的最优解大于0的分量对应着支持向量。a解出来后w也可以解
5、代入一个支持向量,就可以把b求出来
分离超平面就求出来了,加个sign()就是分类决策函数
但是不是什么时候数据都是线性可分的,有些噪音和特异点会让数据线性不可分,这时候就要引进软间隔
软间隔最大化
1、请写出线性不可分情况下SVM的学习问题:
优化目标的两层含义:间隔尽量大,不满足约束样本尽可能少
里面要设定惩罚参数C(是个超参数)
同样通过拉格朗日对偶和KKT条件求解,请自己证明一遍~
解出最优解a后,a的分量a*大于零时是支持向量。对于支持向量如果小于C,epsilon=0该点在间隔边界上;如果等于C,epsilon在01之间,该点在间隔边界和超平面之间。如果等于C,epsilon=1,该点在超平面上。如果此时epsilon>1,分类错误。
软间隔最大化还有其他的求解思路,目标函数设置为:最大化间隔的同时,让不满足约束的样本尽可能的少。最小化该目标函数的结果就是最终解。
2、请写出另解的最优化问题
引入hinge loss 0/1损失
这样我们就可以得到SVM模型的更一般形式
3、请写出SVM模型的更一般形式
两部分组成:结构风险,描述模型的性质和正则化项;经验风险,描述模型与训练数据的契合程度。
我们对这两个部分进行改进就可以得到其他的学习模型LR啊LASSO啊之类的。
软间隔是解决线性不可分问题的方式之一,但是还有很多的问题是软间隔也解决不了的线性不可分问题。这时候我们可以将样本从原始空间映射到更高维的特征空间,使得样本在那个线性空间中线性可分。这就是想要改进模型时比较容易提出的kernel核函数版。
核函数与核方法
1、请写出核函数映射后的对偶问题和划分超平面
样本通过转化函数映射后的向量一般是无限维,因为对偶问题里有转化函数的内积,我们将转化函数的内积称为核函数。如果核函数知道,那么优化依然可以解。
Mercer定理:对称函数的核矩阵半正定,就可以用来当作核函数用。
2、核函数有什么性质?利用的时候要注意什么?
特征空间选择对于SVM性能至关重要。所以在没有确定特征空间,没有得到映射向量的情况下很难确定用什么样的核函数。情况不明确时我们可以先用高斯核。
3、请写一下核函数表示定理
SVM学到的模型可以表示成核函数的线性组合(不考虑偏移项b)
这表示核函数适用于一般的损失函数和正则项,所以可以得到很多线性模型的核化版本
支持向量因为可以化简计算量而且他的解可以非常快的通过SMO解出,那么我们是不是也可以让这种支持向量的思想应用于回归问题呢?
支持向量回归SVR
1、思想、作用、优缺点
思想:保证所有样本落在2e区间内,将最远的在2e线上的点视为支持向量,拟合出一条尽可能平的直线。
作用:处理回归问题得到回归模型
优点:快
2、请写出支持向量回归的损失函数和形式化后的问题
落入间隔带的样本不计算损失,让模型获得稀疏性
SVM这一章主要的痛点在于凸优化和矩阵论的求解,引入了核函数让所有的线性模型有了能处理非线性问题的能力。数学玩的够头疼了,下面放松一下,来个轻松愉快的概率分类器:贝叶斯分类器吧~
06 贝叶斯分类器
我们首先来介绍几个术语:
先验概率:反映我们已经掌握了的知识,比如随季节和海域的不同鱼的分布情况
似然概率:特征的类条件概率分布 在分类为w2的情况下,某色泽亮度的概率
1、思想、作用、优缺点
思想:在特征明确情况下比较概率大小确定分类
作用:二分类问题
优点:简单快捷,和决策树和神经网络有媲美的泛化能力
不足:自变量特征一定要是独立的才可以,否则无法运用;使用极大似然估计的准确性严重依赖于假设的概率分布是否符合潜在的真实数据分布
最小错误率贝叶斯
二类判断问题假设已知鲈鱼和鲑鱼的先验概率,然后知道亮度特征x的似然概率,现在我们手上的这条鱼亮度为x,判断x时鲑鱼还是鲈鱼
通过贝叶斯公式求出在亮度为x的条件下是鲈鱼or鲑鱼的概率,哪个概率大说明是哪个。
Posterior=Likelihood*Prior/Evidence
1、请解释一下最大后验分类规则
最大后验概率规则(等价于期望风险最小化)
2、阐述一下贝叶斯判定准则
为了最小化总体错误率,只要在每个样本上选择能让错误最小的类别标记
例题做一下
上面的问题中我们仅仅是判断类别,并计算错误率,使他最小。但是我们也可以把它应用于其他的行为(不仅仅是判断类别),我们也可以引入损失函数,这样比错误率更有一般性。例题中问一个人呈阳性,是否患病?我们用最小错误率贝叶斯会很自然地将他分成正常人。但实际上会导致所有人都是正常的。这明显不正常好吧,所以要引入损失函数,宁可把正常人分成有病的也不能放过任何一个患病者。
最小风险贝叶斯
1、描述最小风险的判决步骤
给定样本x条件下,计算各类后验概率
求各种判决的条件平均风险
比较各种判决的条件平均风险,把样本归属于条件平均风险最小的判决
2、什么时候最小风险判决规则退化成最小错误率呢?
风险矩阵为分对了0,分错了1的时候
贝叶斯决策论
我们称贝叶斯求解的已知背上不平,问是帝王蟹、松叶蟹的概率后验概率,称已知是帝王蟹、松叶蟹,问背上不平的概率为类条件概率,帝王蟹和松叶蟹的总分布为先验概率。我们思考一下,这个分类器可以分对所有的螃蟹吗?不可以,他会趋近于我们计算出的概率。虽然不是很好但是总比我们选另外一个来的好,错误率低。这种就叫做最小错误率贝叶斯
可以发现想要使用贝叶斯判定准则,必须先获得后验概率。但是真实情况中我们很难直接获得该概率。机器学习要实现的是基于有限的训练样本尽可能准确地估计出后验概率
贝叶斯判定准则:最小化总体风险,在每个样本上选择能让条件风险最小的类别标记
此时称为:贝叶斯最优分类器 对应总体风险为贝叶斯风险
模型精度的理论上限可以通过1-Rh*确定
两种主要策略:判别式模型、生成式模型
1、介绍一下判别式模型
判别式是给定x,然后直接建模后验概率。可以使用决策树 BP神经网络 SVM
2、阐述一下生成式模型
先联合概率,后后验概率,反正就是贝叶斯公式啦
自己想一下贝叶斯公式的各个部分的意义
估计类条件概率经常先假定其具有某种概率分布,然后基于训练样本对概率分布参数估计
模型训练就是参数估计的过程。统计学界的频率派和贝叶斯派有两种不同的认知。
使用极大似然估计进行判定,推一遍吧~这个还挺简单的
3、阐述一下判别式模型
直接后验概率建模
4、对比两种模型
生成式模型
优点:信息丰富,单类问题灵活性强,增量学习,合成缺失数据
缺点:学习过程很复杂,为分布牺牲分类性能
判别式模型
优点:类间的差异清晰,分类边界很灵活,学习简单性能好
缺点:不能反映数据特性,需要全部数据进行学习
生成可以推判别,判别不可以推生成
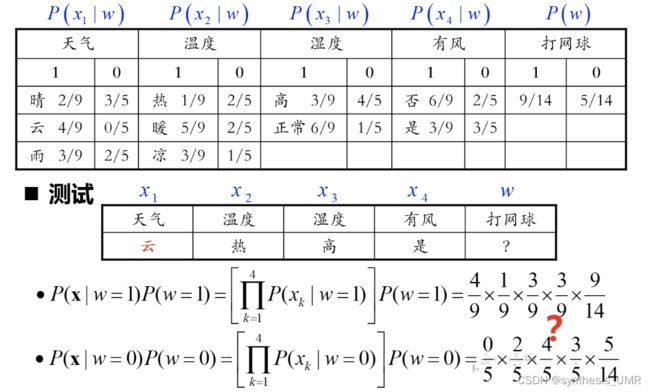
朴素贝叶斯 Naive Bayes
估计后验概率的主要困难在于:类条件概率是所有属性上的联合概率难以从有限的训练样本估计获得
推导推一下
如果只有一个属性的情况下,我们就可以算了,不用进行组合计算,所以变的简单了
例题做一下
拉普拉斯平滑修正
避免其他属性携带的信息被训练集中没有出现的属性值抹去,估计概率时需要进行拉普拉斯修正
因为你是连乘,所以如果有一个项目概率是零就寄了,而且在样本中为0并不代表他一定就是0呀,所以直接分成另一类也是很不对的。因此需要进行平滑修正。
1、朴素贝叶斯分类器常常被用来
查表、懒惰学习、增量学习
半朴素贝叶斯分类器
可以对属性条件独立性假设进行一定程度的放松
最常用的策略是独依赖估计:假设每个属性在类别之外最多仅依赖一个其他属性 默一下公式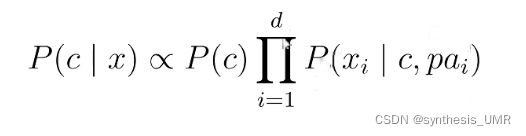
每个属性需要知道父属性才行
SPODE(超级爸爸方法)交叉验证法遍历找出爸爸
AODE方法 给每个属性构建超级爸爸,然后再投票完事儿
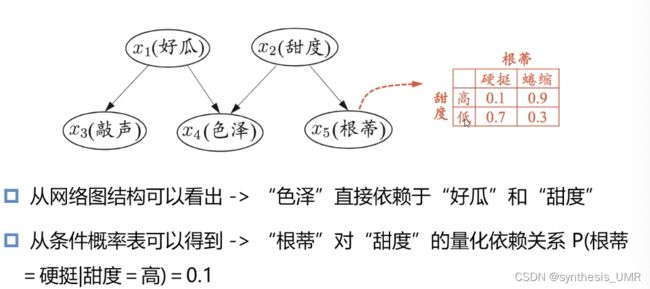
贝叶斯网
信念网,用有向无环图刻画属性之间的依赖关系,并使用条件概率表来表述属性的联合概率分布
存储的是条件概率
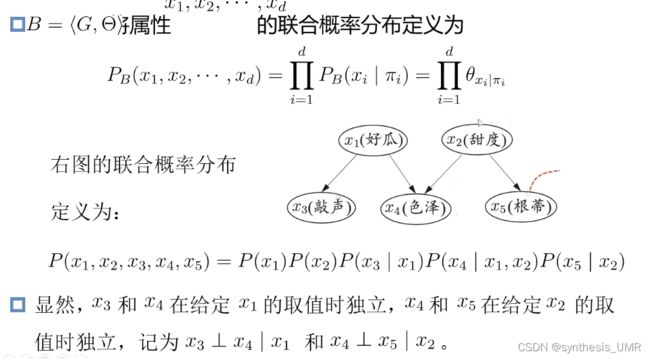
贝叶斯网B有效表达属性之间的条件独立性,给定父节点,贝叶斯网假设每个属性与他的非后裔属性独立:
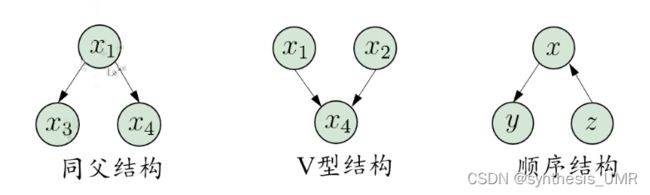
顺序结构中:给定x,yz独立
V型结构:又称冲撞结构,如果给定x4,x1x2肯定不独立;如果x4取值完全未知,x1和x2相互独立
我们称为边际独立性
所以分析图中的条件独立性,可以把有向分离变成无向图,也称道德图:
一个图,一个表,这两个是很难学滴。
EM算法
在现实生活中我们经常遇上缺失属性的样本,那么面对不完整样本我们怎么进行概率模型推断呢?
未观测的变量称为隐变量,构建含有隐变量集的极大似然函数,做极大似然估计就可以求出边际似然。EM算法是常用的估计参数隐变量的方法。
写一下EM算法的过程
我不再需要z具体是什么我在意的是Z的平均性能如何
EM算法是常用的估计参数隐变量的利器。有了sita就能估计Z,有了Z就能估计sita
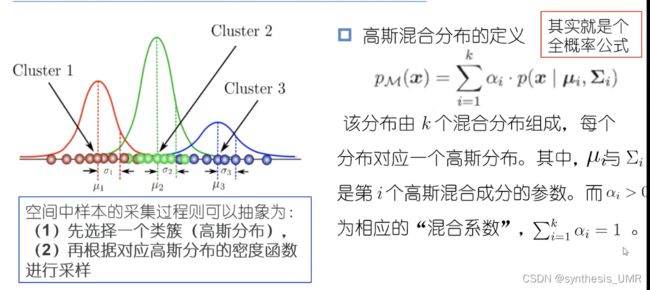
GMM
高斯混合模型
KMeans和LVQ以类中心作为原型指导聚类,高斯混合采用概率模型来表达聚类原型。假设每个类簇中的样本都服从一个多维高斯分布,那么空间中的样本可以看做由k个多维高斯分布混合而成。
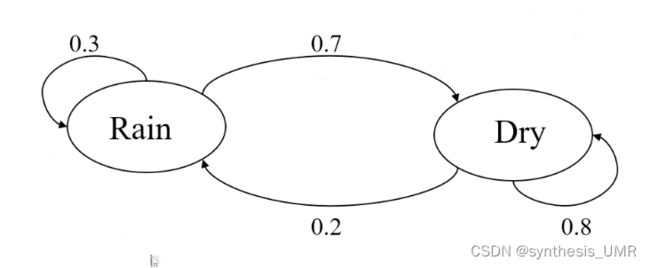
HMM隐马尔可夫
贝叶斯网:图&属性,马尔可夫模型:
状态之间具有序列先后关系,马尔可夫链性质:无记忆性,只和前面一个状态相关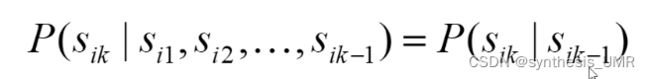
所以可以推导:
隐马尔可夫是啥呢?
通俗易懂讲解HMM(隐马尔可夫模型)_Charles' home-CSDN博客_隐马尔可夫模型详解
A B pai:状态转移矩阵,状态先验概率,观测概率
pai(Si):一开始在Si状态的概率
A:状态转移矩阵P*P矩阵,aij与t没有关系,(语音识别:MFCC)后一刻转移的状态只和前一时刻有关,这就是马尔可夫链假说。
B:若输入向量O属于Sj,则他的概率分布用bj表示。传统的方法,用高斯混合模型来估计bj0
接下来要研究3个问题:
1、识别问题(给出一串序列O=O1O2....On,给出一个HMM模型,给出ABpai,求P(O|lamda)后验概率哪个大就选哪个)
贝叶斯,也不容易啊。。。虽然跟决策树的题目比较像,但是在理解的时候问题还是挺多的。好的,下面我们来个有趣的画圈圈问题:聚类吧~
07 聚类
聚类将数据中的样本划分为若干个通常不相交的子集(簇)。是一种典型的无监督学习
它可以作为单独的过程,也可以作为分类等其他任务的前驱
一类数据可能有很多的分类方法,我们怎么选出最好的分类呢?那么就要度量不同聚类的性能。我们希望同一簇的样本尽可能彼此相似,不同簇的样本尽可能不同。
1、请介绍一下常用的外部指标
通过参考模型得出的SSDD模型,Jaccard系数,FM指数,Rnd指数(后三个在0~1内越大越好)
2、介绍一下常用的内部指标
簇内样本间的平均距离
簇内样本间的最远距离
簇与簇最近样本间的距离
簇与簇中心点间的距离
DB指数越小越好
Dunn指数越大越好
我们现在认为相似性和不同性可以通过dist来判断,距离有很多不同的计算方法。闵可夫斯基距离,欧氏距离,曼哈顿距离等。但是它们都具有一些特性,下面我们介绍一下:
距离度量具有非负性,同一性,对称性,直递性
连续,离散属性;有序属性,无序属性
为了处理无序属性,我们使用VDM方法 属性u上两个离散值a和b之间的VDM距离
但是无序属性距离经常不满足直递性,即非度量距离。
距离不一定是提前定义好的。可以根据数据样本进行动态学习,即距离度量学习
接下来我们来学习几种常见的聚类方式,他们都有非常经典的想法和数学推导
原型聚类
基于原型的聚类,假设聚类结构可以通过一组原型刻画。通常算法先对原型进行初始化,再对原型进行迭代更新。kmeans,LVQ,GMM
1、介绍一下kmeans
找离的最近的,更新簇划分和中心,然后迭代
优点:原理简单,容易实现,可解释性强
缺点:k值难以确定,可能局部最优,对噪音敏感,聚类效果依赖于初始化,对非凸数据效果不好
2、混合高斯聚类
采用概率模型来表达聚类原型
请写出多元高斯分布和高斯混合分布的公式
步骤看这个:
【机器学习】聚类算法——高斯混合聚类(理论+图解)_魏宝航-CSDN博客_高斯混合聚类算法
密度聚类
该类算法假设聚类结构能够通过样本分布的紧密程度来确定。密度聚类从样本密度的角度考虑样本之间的可连接性。基于可连接样本不断扩展聚类簇来获得最终的聚类结果
DBSCAN
1、基本概念
e邻域,核心对象,密度直达,密度可达,密度相连
簇定义:由密度可达关系导出的最大密度相连样本集合
对簇的形式化描述:给定领域参数,簇是满足连接性和最大性的非空样本子集
连接性:xixj都属于C,xixj密度相连,最大型:xi属于C,xi xj密度可达,说明xj也属于C
若x是核心对象,由x密度可达的所有样本组成的集合记为X包含所有由x密度可达的x',则X为满足连接性和最大性的簇
2、算法步骤
遍历样本找出数据集中的核心对象集
根据密度可达,每次循环生成一个簇
优点:对于噪声点有一定抗性
层次聚类
在不同层次对数据集进行划分,从而形成树形的聚类结果。
数据集划分可以采用自底向上和自顶向下两种策略
AGNES
自底向上的层次聚类算法,将样本中的每一个样本看作一个初始聚类簇,然后在算法运行的每一步中找到距离最近的两个聚类簇进行合并。有三种度量方式:
最小距离
最大距离
平均距离
还是很简单滴
聚类真是太善良了,对我们非常滴友善。下面来做一个需要数学推导的吧,集成学习是个非常反直觉的东西。“恕我直言,在座的各位,都是渣渣”,但是一堆只比猜好一点点的分类器居然可以通过集成学习变成极其强悍的强分类器?!
08 集成学习
我们采取投票法进行判断,如果对于一个分类的投票过半,那么就选这个分类。假设每个模型准确率51%,3个子模型集合就可以提升到51.5%,如果子模型60%准确,500个合成就可以到达99.999%的准确率
想要集群起作用,我们认为集成个体应该好而不同。
1、请推导个体集成的关系
总的来说:再基学习器的误差相互独立的条件下,通过增加基学习器的个数可以使错误率指数下降
2、集成学习分两大类,是怎么分的呢?
如果学习器之间存在强依赖,串行生成序列化方法:boosting
如果学习器之间不存在强依赖,可以同时生成的并行化方法:bagging random forest
Bagging 自主采样法
并行式集成学习方法最著名的代表。
思想:并行构建T个分类器,并行训练。最终将所有结果平均或投票,达到最终的预测结果。
1、请讲述自主采样法
给定包含m个样本的数据集,采样产生D'
每次随机挑选样本copy放入D,然后再放回D中使他在下次采样时仍可能被采到
过程重复执行m次,我们得到包含m个样本的数据集
D中有一部分样本会在D'中多次出现,m次采样中始终采不到的概率是第二个重要极限,1/e,取极限得0.368
2、bagging算法的特点
时间复杂度低,bagging集成和直接使用基学习器的复杂度同阶
直接适用于多分类,回归等任务
可以使用包外估计:剩下的36.8%的样本可以用来作验证集对泛化性能进行包外估计
3、包外估计是什么?
首先我们需要记录每个基学习器使用的训练样本Dt,然后仅仅考虑那些没有使用的样本x训练的基学习器再x上的预测
随机森林Random Forest
bagging的一个扩展变种,和bagging一样采样具有随机性,传统的决策树在当前节点的所有属性中选择一个最佳属性;但是RF对于基决策树的每个节点,先从该节点的属性中随机选择一个包含k个属性的子集,再从中选出一个最优属性用来划分。
Bagging仅仅通过样本扰动产生,随机森林中还增加了属性扰动,让最终性能通过个体学习器的差异继续提升。所以在分类器足够多的情况下可以获得比bagging更好的结果。
Boosting
相比于bagging的并行方法,boosting是串行生成的。
思想:提高弱分类器分错样本的权值,降低分对样本的权值,作为下一轮基本分类器的训练样本。表决的时候加大误差率小的分类器。
作用:二分类问题
优点:适用于个体学习器存在强依赖关系的情况
缺点:
1、请阐述boosting的基本算法过程
输入带标签的数组
输出一个最终的分类器Gx
1)训练数据权值初始化 1/N
2)训练数据集得到基本分类器
3)计算分类误差率 计算各个问题的系数
4)更新训练数据集权值分布(公式默一下)
5)构建基本分类器的线性组合
得到最终分类器
Adaboost
最小化指数损失函数:0/1损失的一致性替代损失函数
1、试着推导为什么指数损失函数最小化,分类错误率也最小化
adaboost算法的推导,知道个大概就挺好
2、adaboost特点
优点:不易过拟合,可以使用不同学习算法进行弱分类器构建,adaboost考虑到每个分类器的权重,参数少(学习迭代次数)
缺点:弱分类器数目不好设定,可以使用交叉验证
对于异常样本敏感,异常样本在迭代中权重较高,影响预测准确性。
原始adaboost不适用于处理多分类和回归任务,训练耗时长
3、偏差方差分解角度
boosting降低偏差,对于泛化能力弱的学习器构造出很强的集成
结合策略
最后获得的线性学习器是弱学习器的线性组合。我们来介绍一下几种分类方法:
1、简单平均法 2、加权平均法
集成学习中各种结合方法都可以看成加权平均法的变种
加权平均法不一定优于简单平均法,因为样本不充分或者有噪音,导致学出来的权重不完全可靠
3、投票法
绝对多数投票法 必须要占到50%以上
相对多数投票法 得到最多的票数就可以
加权投票法
要注意不同类型的损失还舒适不可以混用的哦
4、学习法
更加高级,学习出一种投票的学习器。代表为Stacking。
多样性
我们来理解一下好而不同究竟是怎么一回事儿
1、请你写出误差-分歧分解的公式
个体学习器精确性越高,多样性越大,则继承效果越好。
2、多样性度量的方法
K Q统计量、可以通过数据样本扰动,输入属性扰动,输出表示扰动,算法参数扰动等方法增强学习器的多样性。
数据样本的扰动是基于采样法:bagging中的自主采样,adaboost中的序列采样
不稳定的对于数据样本扰动敏感的基学习器:决策树,神经网络等
稳定的基学习器:线性,SVM naive bayes KNN
09 降维与度量学习
kNN
1、思路,作用,优点
思路:我们可以找到训练集中距离最近的k个样本,对于分类问题我们使用投票法,对于回归问题我们使用平均法。还可以基于距离远近进行加权平均或加权投票,距离越近的样本权重越大
作用:常用的监督学习方法,明显的懒惰学习
优点:超级简单
缺点:依赖于k的值
2、什么是懒惰学习?什么是急切学习?
此类学习技术在训练的阶段只是把样本保存起来,训练开销为0,等到收到测试样本后再进行处理。相对的急切学习:在训练阶段就对样本进行学习处理。
我们来理论分析一下kNN的性能,首先写一下 1NN二分类错误率
假设iid 密采样,然后结合贝叶斯最优概率,发现泛化误差不超过最好的2倍。
但是这是不够的,因为密采样会导致维数灾难。
一般情况下如果现有特征获得的分类器性能不行,考虑添加新的特征,来提高分类器性能。(以运算复杂度为代价)分类器的准确度和运算复杂度trade off
比如:两个密度函数在三维空间内没有交集,其在一维和二维空间中存在交集,所以贝叶斯分类器在一二维空间存在误差。理论上添加新特征提供了额外的信息。分类器性能提高。
但是我们不能无限制增加,因为样本需求会指数级增加。
我们现在知道了高维度是有好处的,但是很难用。所以我们如何应对高维特征呢?既不能全部都用,也不可以全部都扔掉。那我们可以使用几个重要的点。这里我们终于引出了特征降维。用来保留主要的信息量。
09 主成分分析PCA
Principal component analysis
线性降维方法,对原始高维空间进行线性变换
思想:想要获得低维子空间,可以对原始高维空间线性变换。新空间中的样本是原空间中的线性组合而不是进行了特征选择,所以保留了全部信息。
利用线性变化进行降维是线性降维方法。对低纬子空间性质的不同要求可通过对W施加不同的约束实现。
以前我们学的LDA是线性有监督的。PCA是线性无监督的降维。这两个要进行比较着看。
优点:对于线性结构分布的数据集有较好的降维效果。在压缩,降噪,数据可视化方面非常有效。计算简单容易理解。
缺点:对于结构非线性和属性强关联的数据集无法发现他的内在本质结构。
对于正交属性空间中的样本点,如何用一个超平面对所有样本进行恰当的表达?我们要找到超平面的方向。
如果存在这样的超平面,他可能具有:
1.最近重构性 样本点到超平面的距离都足够近
2.最大可分性 样本点在超平面上的投影尽可能分开
这两者是等价的,推导出来结果相同。
2、最大可分性推导
https://zhuanlan.zhihu.com/p/77151308
3、最近重构性推导
4、PCA过程
输入样本集和低维空间维数d',输出投影矩阵W
对所有样本进行中心化,然后计算样本的协方差矩阵,再对协方差矩阵作特征值分解,最后取最大的d‘个特征值所对应的特征向量组成投影矩阵W
如果均值不为0最后会有一个偏置,所以我们中心化。
5、特点
降维后的低维空间的维度数通常是用户事先指定的。我们可以先用KNN交叉验证一下选择较好的d'
PCA还可以选择重构阈值,留下的维度越多重构的越好,我们用能量(我们所选定的特征值的和和原来所有特征值的和的比值)来衡量,一般95%。
降维会导致信息损失,但是一方面采样密度大,另一方面数据受到噪声影响,最小的特征值对应的特征向量往往和噪声有关。舍弃最小特征值可以降噪。
核化线性降维:KPCA
线性方法假设映射是线性的,但是现实中需要非线性映射才能找到恰当的低维嵌入
假设我们将在高维特征空间中把数据投影到由W确定的超平面上
那么映射向量zi就是xi在高维特征空间中的像 先升后降后希望比xi维度低
(特征值此时不能是0 ,但是我们是从大到小取的所以默认0已经没有放进来了)ai是标量,W是个d*1维向量。所以W变成了所有样本点映射后的线性组合。
根据表示定理,说明PCA一定可以进行核化。因为问题已经变成求a了,而且他们是原始样本的线性组合问题。
zi是通过原始属性空间中xi通过映射fai产生,如果fai可以显式表达出来,通过它将样本映射到高维空间,再在特征向量中实行PCA,有:
一般情况下我们不知道映射函数fai的具体形式,引入核函数k(xi,xj),将上图中2式代入1式,获得KA=lamdaA,K是k对应核矩阵,A是ai构成的矩阵。
 上面这个就是特征值分解问题,直接取K最大的d'个特征值就可以得到对应特征向量。
上面这个就是特征值分解问题,直接取K最大的d'个特征值就可以得到对应特征向量。
现在我们得到模型了,那如果我们得到一个新的样本怎么办呢?以往PCA降维关键在于W,我们得到新样本后左乘一个W就完事儿了。KPCA稍微复杂一点儿。
对于新样本x,投影后第j维坐标为上式,升维空间faix再左乘wj降维。然后wj可以写成ai的线性加和,带入得到了第j维的坐标为所有样本点核函数的加和乘上系数ai。这个比PCA更加耗费时间。
流形学习
manifold
流形是线性子空间的一种非线性推广,从拓扑学角度:局部区域线性,与低维欧氏空间拓扑同胚
局部有欧氏空间性质,可以使用欧氏距离进行距离计算。
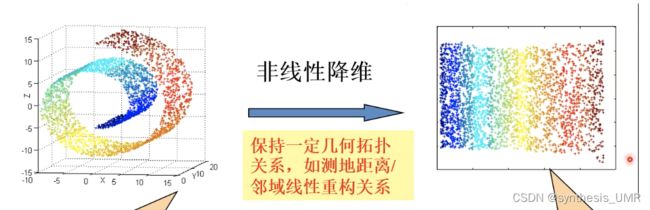
流形学习可以从高维采样数据恢复低维流形结构,是一种非线性降维方法
流形学习可能是人类认知中一种自然的行为方式,流形是感知的基础,人类具有捕捉的能力
Isomap全局特性保存
等度量映射
1、作用,思想,优缺点
作用:特征降维
思想:低维流形嵌入高维空间后,直接在高维空间计算直线距离不合适。因为高维空间中直线距离在低维嵌入流形上不可达,所以引入本真距离:测地线距离。
优点:简单
弱点:大问题,他只能单向从训练样本映射到降维空间。但是如果新的样本输入缺少参数。所以我们还得训练一个学习器来回归。
2、测地距离
较远点之间测地距离通过最短路径确定,较近点之间通过欧式距离替代
测地距离反应数据在流形上真实距离差异
3、算法过程
输入样本集、近邻参数,低维空间维度d‘
过程:确定每个点的k近邻,xi与k近邻点之间距离设置为欧氏距离,与其他点设置为无穷大
调用最短路径计算dist,将xi xj作为MDS算法输入(多维缩放算法),返回MDS输出。
输出样本集合D在低维空间的投影Z
LLE局部特性保存
locally Linear Embedding
局部线性嵌入试图保持邻域内的线性关系,并使得该线性关系在降维后的空间中继续保持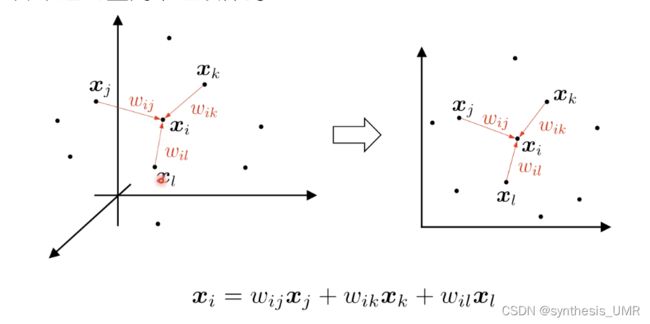
LLE的学习目标就是降维之后需要保持同样系数的关系
1、构建过程
先给每个样本找到他的近邻下标集合,然后计算出基于Qi中的样本点对于xi进行线性重构的系数wi,其中xixj已知,令一个Cjk,可以算出wij有闭式解
LLE在低维空间中保持系数wi不变,于是xi对应的低维空间坐标zi可以求解一个优化问题
2、算法步骤
输入:样本集,近邻参数k,低维空间维度d‘
过程:确定xi的k近邻,求出重构系数。求出M,取M特征向量最小的d‘个值就可以了
度量学习
降维的本质是什么,实际上就是在找一个合适的距离度量(通过降维的方法)
想要学习距离,就必须给定一个自由度:平方欧式距离。对于两个d维样本,有:![]()
所以就是各个维度下两点的距离。如果不同属性的重要程度不一样 我们可以采用加权的方法:
W是对角矩阵,里面存储权重wi
W的非对角元素为0,所以坐标轴是正交的,属性之间无关系。但现实中很多属性之间有各种关系。所以我们将W替换成一个普通的半正定矩阵M,得到马氏距离 ![]()
M称为度量矩阵,度量学习就是对M进行学习,M必须是半正定对称矩阵
差不多完事儿了,最后两章,神经网络稍微讲一下,深度学习下学期详细弄
10 半监督学习SSL(科普式)
大数据时代,数据量虽然多了,但是标记这些数据实在是太抓狂了而且有些数据还需要专家标记。为啥大家不爱打标签?嫌费事儿啊。我们可不可以利用很少的标记和很多的未标记数据?
主动学习
对于无标记的样本,首先呢,先用有标记学一个模型出来,然后拿着无标记样本中最不错的瓜去问标记者,然后我们加入标记组再进行学习。这个过程叫查询,我们希望查询次数尽量少。如果不和专家交互,还能利用为标记嘛?
监督学习的情况下,我们可以按照他离正负哪个近选哪个。但如果他到正负一样近咋办?半监督学习中,我们可以使用旁边那些个没有标记的点。如果那一堆都是正or负,那就归类成正or负吧~
The distribution of the unlabeled data tell us sth
要利用未标记样本,肯定要做一些将未标记样本所揭示的数据分布信息与类别标记相联系的假设,其中有两种常见的假设。都希望相似样本有相似的输出那就好了。
(1)聚类假设
假设数据存在簇结构,同一个簇里面的数据是同一类的。
(2)流形假设 可以看做聚类假设的推广
假设数据分布在流形结构上,邻近样本具有相似输出值。
两种半监督学习的思路:
纯半监督学习(基于开放世界):
我们发现无标记样本和待测数据没啥区别,都长得一样只不过人为分类成了不同的用途
直推式学习(基于封闭世界):
在无标记的训练样本上达到一个很好的性能,认为无标记样本就是整个世界。(但是我们测试的话还是需要引入测试样本滴)
半监督SVM
首先要正确区分有标记样本不同类别,随后要求穿过样本密度最低的部分。怎么找?Transductive SVM 直推式SVM。他是怎么利用无标记样本点的?
TSVM
针对二分类问题,TSVM考虑对未标记样本进行各种可能的标记指派,在所有结果中,寻找一个在所有样本上间隔最大化的划分超平面 。个么这是一个穷举过程,这个解法效率太低了。
Cu是面向未标记样本的,引入 yi hat,一个伪标记。变成软间隔最大化的标准形态。在所有可能中找到一个间隔最大的超平面。
TSVM采用局部搜索来迭代寻找近似解。首先用有标记样本训练SVM0,接下来通过他去给无标记样本给样本增加一个伪标记。接下来再用带伪标记的无标记样本和有标记样本一起训练得到SVM1。然后在无标记样本上进行搜索,找到一对最有可能出错的样本,然后交换样本标记。这两个样本应该是距离SVM1最近的两个样本,交换两个样本的标记,然后再训练SVM2,不断迭代,直到达成正确分类和软间隔为0。
两个参数Cu Cl,谁大谁小比较好?伪标记一般不对,所以Cu< 搜索标记指派可能出错的样本仍然是一个大规模优化问题,所以半监督SVM的研究重点是如何设计出高效的优化求解策略。 使用多学习器,而学习器之间的分歧对于未标记数据的利用非常重要 协同学习最初是针对多视图设计的 multi-view:各个方向各个种类的信息 协同训练:多视图间有相容互补性,设数据有两个充分且条件独立的视图,每个属性集都足够描述该样本,且互相独立。互相把自己最确信的样本送给另一个进行训练,从而进行模型的更新。x1x2描述的是同一个样本,会配备一个y标记,没有标记的样本有x1x2的描述但是没有y,需要得到一个y hat。 若两个视图充分且条件独立,则可利用未标记样本通过协同训练可以将若分类器的泛化性能提升到任意高。条件独立性一般很难满足,但是条件弱的情况下协同训练还是可以有效提升弱分类器性能。 单视图数据也获得了一些变体算法。他们或是使用不同学习方法,或使用不同的数据采样,甚至使用不同的参数设置来产生不同的学习器,也能有效地利用未标记数据来提升性能。 只要弱分类器之间具有显著的分歧,就可以互相为对方提供伪标记从而提升性能。 聚类是无监督学习任务,但是现实中我们可以提供一些额外信息。 第一种:must link;cannot link,指样本必属于一个or必定不属于一个簇 第二种:少量的有标记样本 约束k均值算法是利用第一种监督信息的代表(原型聚类) 需要检测划分后是否会违背额外信息的约束规定 第二种监督信息用起来很简单,直接把他们作为种子,用他们初始化kmeans聚类中心。并且在聚类簇迭代更新过程中不改变种子样本的簇隶属关系。 1、发展历史 第一阶段: 第二阶段: 卷积神经网络需要大量数据和高速GPU。 M-P神经元模型 输入来自其他n个神经元传输过来的信号 处理输入信号通过带权重的链接进行传递,神经元接收到总输入值将与神经元的阈值进行比较 假设二分类问题, 那么f最好是阶跃函数,用Sigmoid函数族替代。我们发现这个神经元模型的输出函数。。。和logistic模型怎么这么像啊 由两层神经元组成,输入层接受外界信号输入传递给输出层,输出层是M-P神经元(注意输入层x1x2没有进行变换,输出层是一个典型的MP神经元) 感知机很容易实现与或非运算(参数有无数组取值) 与:比如w1 w2=1,sita=2 或:w1 w2=1,sita=0.5 非:w1=-0.6 w2=0 sita=-0.5 机器怎么学习这些参数? 感知机和其他线性分类器的区别在哪儿?找w和b的方式不同。感知机的损失函数是: 这个lost function一定是正的,而且是w,b的连续可导函数(给定训练数据集T) 如果没有误分类点,损失函数为0,误分类点越少,误分类点距离超平面越近,损失函数越小 学习规则:随机梯度下降法 随机选一个样本点,如果对于损失函数没有影响不更新,有影响更新。目标在于找到wb使误分类率为0。 当训练集线性可分时,算法收敛有无数个解 当训练集线性不可分时,学习过程发生震荡怎么办呢?多层感知机和神经网络 这些神经元的链接是事先排好的,也就是超参数。我们来看一种全链接神经网络 黄输入,绿偏置b,圈function deep=many layers 怎么找里面的网络结构?怎么确定?不知道。。。所以神经网络的理论还不完善 损失函数: 然后要计算total loss,最后使用梯度下降方法进行参数筛选。 计算梯度的时候比较有效率的方式,限定对于neural network进行操作。 network的参数里面主要是w和b,把他们的初始值记为sita0,然后计算sita0的梯度。 前传一次,反传一次,就可以把所有的参数都算出来。 复习了4天到了考试前,基本上推导都已经掌握了。最后记录一下边角料吧~ 图像生成与编辑 妆容分析 音视频协同计算 跨光谱合成(红外相机拍出来的) 图形识别,图像哈希 多媒体内容安全,从哪儿来,是否被篡改,如何篡改的? 人工智能安全,情感计算 手机屏幕检测 好了,就到这儿了,快去学数学!!! 完基于分歧的方法
半监督聚类
11 神经网络基础
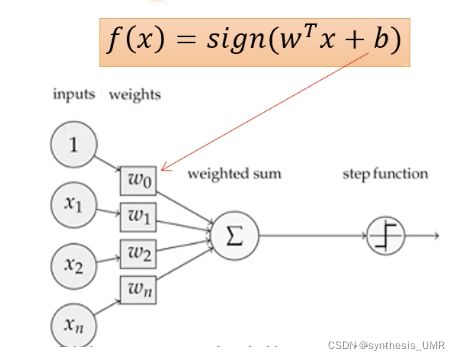
神经元模型

感知机
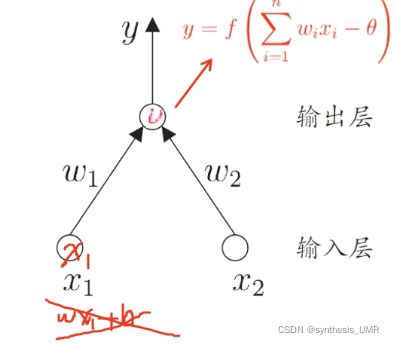
![]()
反向传播算法
机器学习应用场景