Python数据结构学习笔记——搜索与排序算法
目录
- 一、搜索
-
- (一)搜索的方法
- (二)顺序搜索
- (三)二分搜索
- 二、排序
-
- 内排序和外排序
- (一)冒泡排序
- (二)选择排序
- (三)插入排序
- (四)希尔排序
- (五)归并排序
- (六)快速排序
- 总结
一、搜索
(一)搜索的方法
搜索是指从元素集合中找到某个特定元素的算法过程,搜索过程通常返回True或False,分别表示元素是否存在。Python中通过运算符in来检查一个元素是否处于元素集合中,如下:
print("C" in ["C", "S", "D", "N"])
print("C" in (1, 2, 3))
print("c" in {"a": "A", "b": "B", "c": "C"})
print("c" in {1, "123", "ab"})
(二)顺序搜索
以python中的列表为例,由于其各元素存在线性或顺序的关系,每个元素都有一个唯一的下标,且下标是有序的,可以通过顺序访问,从而进行顺序搜索。顺序搜索的概念是从左到右依次查找元素,从第一个元素开始依次,若到列表末尾仍没有查到则说明该元素不在列表中。
无序列表的顺序搜索和有序列表的顺序搜索的时间复杂度都是O(n),只有当列表中不存在要搜索的目标元素时,有序排列的元素的顺序搜索的效率较高。
无序列表的顺序搜索代码如下:
# 无序列表的顺序搜索
def sequential_Search(alist, item): # 传入两个参数:一个无序列表及要搜索的元素
pos = 0 # 下标值从0开始
found = False
while pos < len(alist) and not found: # 直到搜索到元素循环停止
if alist[pos] == item: # 若当前下标值对应的元素等于要搜索的元素,found变量值为True
found = True
else:
pos = pos + 1 # 下标值加一,继续搜索
return found
# 有序列表的顺序搜索
def orderedSequential_Search(alist, item): # 传入两个参数:一个有序列表及要搜索的元素
pos = 0 # 下标值从0开始
found = False
stop = False
while pos < len(alist) and not found and not stop:
if alist[pos] == item: # 若当前下标值对应的元素等于要搜索的元素,found变量等于True
found = True
else:
if alist[pos] > item: # 若当前下标值大于要搜索的元素,则stop变量等于True
stop = True
else:
pos = pos + 1 # 下标值加一,继续搜索
return found
print(sequential_Search([6, 4, 5, 0], 6))
print(orderedSequential_Search([1, 2, 3, 4, 5], 6))
(三)二分搜索
二分搜索相较于顺序搜索,其不是从第一个元素开始搜索列表,而是从中间的元素着手,所以被称为二分搜索。若这个元素就是要搜索的目标元素,则立即停止搜索;如果不是,则可以利用列表有序的特性,排除一半的元素,依次下去,直到搜索到目标元素。简单的来说,也就是将一个大问题依次分成小问题,从而缩小范围,依次解决。
对于有序列表来说,二分搜索算法在最坏情况下的时间复杂度是O(logn),有序列表的二分搜索代码如下:
# 有序列表的二分搜索
def binarySearch(alist, item): # 传入两个参数:一个有序列表及要搜索的元素
first = 0
last = len(alist) - 1 # 列表的最后一个元素的下标值
found = False
while first <= last and not found:
midpoint = (first + last) // 2 # 整除进行二分
if alist[midpoint] == item:
found = True
else:
if item < alist[midpoint]:
last = midpoint - 1
else:
first = midpoint + 1
return found
print(binarySearch([1, 6, 9, 10, 13, 14, 18], 14))
运行结果如下:

步骤解析:

二分搜索中运用递归方法进行改进,代码如下:
#二分搜索的递归方法
def binarySearch(alist, item):
if len(alist) == 0:
return False
else:
midpoint = len(alist) // 2
if alist[midpoint] == item:
return True
else:
if item < alist[midpoint]:
return binarySearch(alist[:midpoint], item) # alist[:midpoint]表示从开头取到midpoint下标值
else:
return binarySearch(alist[midpoint + 1:], item) #alist[midpoint + 1:]表示从结尾取到midpoint+1下标值
print(binarySearch([1, 6, 9, 10, 13, 14, 18], 14))
二、排序
内排序和外排序
根据待排序的内容是否在内存中可将排序分为内排序和外排序,内排序的整个排序过程在内存在进行,而外排序由于排序的内容太多,内存无法容纳,需要借助外存,即其排序过程在内、外存之间交换数据才能进行。
(一)冒泡排序
冒泡排序通过两两比较相邻元素,如果反序,即大的在前面小的在后面时则交换,小的元素被交换至前面,一直到没有反序的情况为止,之所以叫做冒泡排序是因为在排序过程中,越小的元素会经过交换像一个个气泡一样浮到水面,即最小的元素会到数列的最前面,而最大的元素将会沉到数列的最底端。
冒泡排序中无论元素如何排列,给含有n个元素的列表进行冒泡排序需遍历n-1轮,该算法的时间复杂度是O(n2),其中最好情况下,列表已处于有序不需要执行交换操作;而最坏情况下,每一次比较都将导致一次交换。
冒泡排序的程序代码如下:
#冒泡排序
def BubbleSort(alist):
for passnum in range(len(alist) - 1, 0, -1): # range()函数中取列表的长度减一至0,每次循环-1
for i in range(passnum):
if alist[i] > alist[i + 1]: # 若列表中下标为i的元素大于下标为i+1的元素,则执行以下操作交换两个变量
temp = alist[i] # 中间变量temp存储下标为i的元素
alist[i] = alist[i + 1] # 交换两个元素
alist[i + 1] = temp # 中间变量temp赋值给下标为i+1的元素
print(alist)
BubbleSort([3, 0, 1, 9, 10, -2])
运行结果如下:
![]()
具体的执行步骤如下:

1、由于python的特性,通过同时赋值将交换的三行语句直接替换为一条语句:
temp = alist[i]
alist[i] = alist[i + 1]
alist[i + 1] = temp
替换为a,b=b,a的形式,从而直接交换:
alist[i], alist[i + 1] = alist[i + 1], alist[i]
def BubbleSort(alist):
for passnum in range(len(alist) - 1, 0, -1): # range()函数中取列表的长度减一至0,每次循环-1
for i in range(passnum):
if alist[i] > alist[i + 1]: # 若列表中下标为i的元素大于下标为i+1的元素,则执行以下操作交换两个变量
alist[i], alist[i + 1] = alist[i + 1], alist[i] # 直接使用一条语句进行交换
print(alist)
BubbleSort([3, 0, 1, 9, 10, -2])
运行结果如下:
![]()
2、短冒泡
冒泡排序的效率很低,因为在确定最终的位置前必须交换元素,它遍历了列表中未排序的部分。
若在一轮遍历中没有产生交换,则可以说明列表中的元素已经有序,此时可以通过修改程序使程序终止,称为短冒泡排序,其中变量passnum控制循环的循环次数,从而在遍历中没有产生交换时终止,代码如下:
# 短冒泡排序
def ShortBubbleSort(alist):
exchanges = True # 变量exchanges值一开始为True
passnum = len(alist) - 1 # 变量passnum值为列表长度减一
while passnum > 0 and exchanges:
exchanges = False
for i in range(passnum):
if alist[i] > alist[i + 1]:
exchanges = True
alist[i], alist[i + 1] = alist[i + 1], alist[i]
passnum = passnum - 1
print(alist)
ShortBubbleSort([3, 0, 1, 9, 10, -2])
(二)选择排序
选择排序每次遍历列表时只做一次交换,在每次遍历时寻找最大值,并在遍历完之后将它放到正确位置上。若给n个元素排序,需要遍历n-1轮,这是因为最后一个元素要到n-1轮遍历后才就位,该算法的时间复杂度也是O(n2)。
选择排序的代码如下:
# 选择排序
def SelectSort(alist):
for i in range(len(alist) - 1, 0, -1): # range()函数中取列表的长度减一至0,每次循环-1
positionOfMax = 0
for location in range(1, i + 1): # 每次遍历列表时进行一次交换
if alist[location] > alist[positionOfMax]:
positionOfMax = location
alist[i], alist[positionOfMax] = alist[positionOfMax], alist[i]
print(alist)
SelectSort([9, 12, 0, -6, 7, 36, 1])
运行结果如下:
![]()
具体的执行步骤如下:
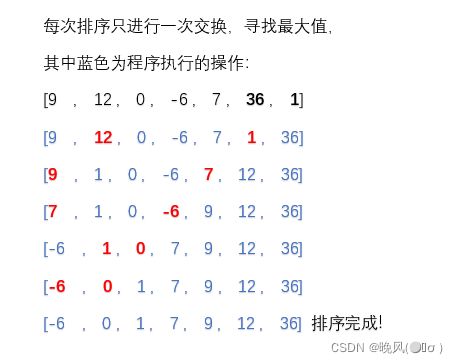
通过将冒泡排序和选择排序比较,排序列表[9, 12, 0, -6, 7, 36, 1],选择排序只交换了5次,而冒泡排序多达十几次,因此选择排序算法通常更快。
(三)插入排序
插入排序的原理是在列表的一端维护一个已有序的子列表,逐个将另一边的元素插入至这个有序的列表中,每轮将当前元素与有序子列表中的元素进行比较,有序子列表中将比它的元素右移,遇到比它小的或到达子列表终点时,就将当前元素插入,最后使整个列表有序化,插入排序的时间复杂度也是O(n2)。
插入排序的代码如下:
# 插入排序
def InsertSort(alist):
for index in range(1, len(alist)): # for循环次数为1至列表的长度-1
currentvalue = alist[index]
position = index
while position > 0 and alist[position - 1] > currentvalue:
alist[position] = alist[position - 1]
position = position - 1
alist[position] = currentvalue
print(alist)
print(InsertSort([2, 0, 9, -3, 1, 4]))
运行结果如下:
![]()
具体的执行步骤如下,左边标红的数字为排列好的顺序:

(四)希尔排序
希尔排序是经插入排序改进后的排序算法,它将排序的列表切分成多个子列表,然后对每一个子列表进行插入排序,其中切分列表使用一个增量(或步长)选取间隔为一定增量的元素组成子列表,增量为sublistcount = len(alist) // 2,然后缩小增量以sublistcount = sublistcount // 2继续切分列表,最后再对此时增量为1的列表进行插入排序。
采用以下代码的希尔排序的时间复杂度是O(n1)至O(n2)之间,希尔排序的程序代码如下:
# 希尔排序
def ShellSort(alist):
sublistcount = len(alist) // 2 # 选取增量为列表长度的2的整除,切分列表
while sublistcount > 0:
for startposition in range(sublistcount):
InsertSort(alist, startposition, sublistcount)
print("当前选取增量:", sublistcount, "当前列表顺序:", alist)
sublistcount = sublistcount // 2 # 继续切分列表
def InsertSort(alist, start, gap): # 插入排序
for i in range(start + gap, len(alist), gap):
currentvalue = alist[i]
position = i
while position > 0 and alist[position - gap] > currentvalue:
alist[position] = alist[position - gap]
position = position - gap
alist[position] = currentvalue
ShellSort([2, 0, 9, -3, 1, 4])
(五)归并排序
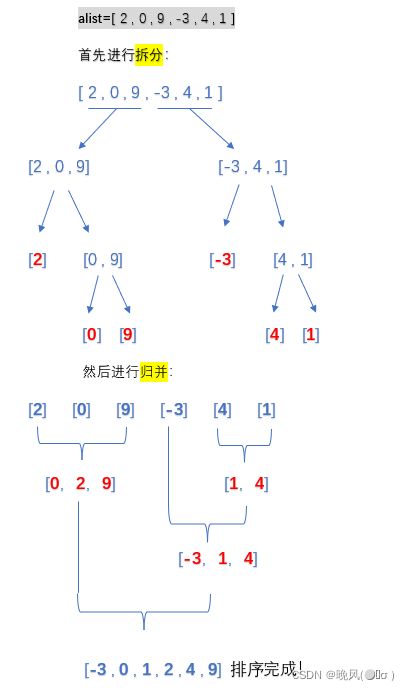
归并排序是一种递归算法,每次操作将当前列表一分为二进行拆分,若分开的子列表为空或只有一个元素时,则可以认为它是有序的;若子列表不为空则再将列表一分为二,对两部分都递归调用归并排序,依次进行下去,当对一分为二的两部分子列表都有序后,再将其归并为一个有序列表,即完成排序。
归并排序的时间复杂度是O(nlogn),但是归并过程需要用到额外的存储空间,归并排序的程序代码如下:
# 归并排序
def MergeSort(alist):
print("切分", alist)
if len(alist) > 1: # 若列表的长度大于1则执行以下代码
mid = len(alist) // 2 # 将当前列表一分为二进行拆分
left_half = alist[:mid] # 拆分后的的左子列表
right_half = alist[mid:] # 拆分后的的右子列表
MergeSort(left_half) # 递归调用自身函数
MergeSort(right_half) # 递归调用自身函数
i, j, k = 0, 0, 0
while i < len(left_half) and j < len(right_half): # 将拆分的列表归并为一个有序列表
if left_half[i] < right_half[j]:
alist[k] = left_half[i]
i = i + 1
else:
alist[k] = right_half[j]
j = j + 1
k = k + 1
while i < len(left_half):
alist[k] = left_half[i]
i = i + 1
k = k + 1
while j < len(right_half):
alist[k] = right_half[j]
j = j + 1
k = k + 1
print("归并 ", alist)
MergeSort([2, 0, 9, -3, 4, 1])
(六)快速排序
和归并排序一样,快速排序也是采用一分为二的方式,但它不会占用额外的存储空间,不过列表可能不会被一分为二从而影响效率。
首先,快速排序会选出一个基准值用于切分列表,也就是分隔点;然后进行分区,将大于基准值和小于基准值的元素放在两边,其中leftmark和rightmark变量代表位于列表中剩余的所有元素的开头元素和末尾元素。
快速排序的程序代码如下:
# 快速排序
def quickSort(alist):
quickSortHelper(alist, 0, len(alist) - 1)
print(alist)
def quickSortHelper(alist, first, last): # 递归函数
if first < last:
splitpoint = partition(alist, first, last)
quickSortHelper(alist, first, splitpoint - 1)
quickSortHelper(alist, splitpoint + 1, last)
def partition(alist, first, last): # 分区函数
pivotvalue = alist[first]
leftmark = first + 1
rightmark = last
done = False
while not done:
while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
leftmark = leftmark + 1
while alist[rightmark] >= pivotvalue and rightmark >= leftmark:
rightmark = rightmark - 1
if rightmark < leftmark:
done = True
else:
alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
alist[first], alist[rightmark] = alist[rightmark], alist[first]
return rightmark
quickSort([2, 7, -1, 0, 9, -3, 4, 1])
总结
| 名称 | 时间复杂度 |
|---|---|
| 顺序搜索 | 不论列表是否有序,都为O(n) |
| 二分搜索 | 对于有序列表,为O(logn) |
| 冒泡排序 | O(n2) |
| 选择排序 | O(n2) |
| 插入排序 | O(n2) |
| 希尔排序 | 介于O(n)和O(n2)之间 |
| 归并排序 | O(nlogn) |
| 快速排序 | O(nlogn),当切分点不靠近列表中部时会降低至O(n2) |