编程实战（2）——Python解微分方程方法总结

编程实战（2）——Python解微分方程方法总结

综述

最近有用python解微分方程的需求，然后找了网上很多的资料和帖子，然后结合个人的想法做了一些研究。

本篇博客主要讲解了二阶常系数微分方程的解析解和数值解的解法以及一阶常系数微分方程组的通解解法，并对每一个步骤做了详细的说明（网上很多帖子讲的并不是很详细），并做了一些探究性的尝试

代码解析

二阶常系数齐次微分方程的解析解

dsolve获取解析解

我们这里用到的库是sympy；

用sympy.dslove常系数齐次微分方程代码思路如下：

• 首先我们要把需要的微分方程化成$g(f(x),x)=0$的形式；
• 然后把所有的可能被求导的自变量找出来，同时确定因变量，用sympy.symbols标记自变量，用Function表示因变量；
• 解方程并输出

例题：解微分方程$f(x{)}^{\prime \prime }+{\omega }^{2}f(x)=0$

现在对照上面的三步很简单的思路来看一个例子：

import sympy as sy

x = sy.symbols("x") # 标出x和ω为自变量并用符号'x'和'w'表示之
omega = sy.symbols("w")
f = sy.Function("f") # 函数因变量f(x)，用f表示

equation = f(x).diff(x,2) + omega**2*f(x) # 化成g(f(x),x) = 0的形式，diff是求导函数

print(sy.dsolve(equation,f(x)))
sy.pprint(sy.dsolve(equation,f(x)))# 两种输出方法，前面一个是返回的真实的dsolve返回的元组，后面是sympy库自带的格式化输出解析解的字符串

输出的结果：

Eq(f(x), C1*exp(-I*w*x) + C2*exp(I*w*x))

           -ⅈ⋅w⋅x       ⅈ⋅w⋅x
f(x) = C₁⋅ℯ       + C₂⋅ℯ   

这个结果可以化成对应的三角函数形式。

检验一下

我们拿同济高数书上第346页上的一道例题来检验一下：求方程 $y^{(4)}-2y^{\prime \prime \prime }+5y^{\prime \prime }=0$的通解。

代码：

import sympy as sy

x = sy.symbols("x")
y = sy.Function("y")

equation = y(x).diff(x,4)-2*y(x).diff(x,3)+5*y(x).diff(x,2)

print(sy.dsolve(equation, y(x)))
sy.pprint(sy.dsolve(equation, y(x)))

输出：

Eq(y(x), C1 + C2*x + (C3*sin(2*x) + C4*cos(2*x))*exp(x))
                                                x
y(x) = C₁ + C₂⋅x + (C₃⋅sin(2⋅x) + C₄⋅cos(2⋅x))⋅ℯ 

对照书上的答案，是正确的。

dsolve能解二阶非齐次微分方程吗？

我们还是拿同济高数书来检验一道例题：求方程通解 $y^{\prime \prime }-5y^{\prime }+6y=x{e}^{2x}$

代码：

import sympy as sy
from math import e

x = sy.symbols("x")
y = sy.Function("y")

equation = y(x).diff(x,2)-5*y(x).diff(x,1)+6*y(x)-x*e**(2*x)

print(sy.dsolve(equation, y(x)))
sy.pprint(sy.dsolve(equation, y(x)))

输出结果：

Eq(y(x), -0.5*7.38905609893065**x*x**2 - 1.0*7.38905609893065**x*x + C1*exp(2*x) + C2*exp(3*x))
                             x  2                       x         2⋅x       3⋅
y(x) = - 0.5⋅7.38905609893065 ⋅x  - 1.0⋅7.38905609893065 ⋅x + C₁⋅ℯ    + C₂⋅ℯ  

x

谜一般的输出，只有$C1\ast exp(2\ast x)+C2\ast exp(3\ast x)$这一部分是跟答案相同的，其他长长的数字就很莫名其妙了。

之所以会有前面那堆奇怪的数字可能跟算法有关系，这里就不再深究了，只能说用dslove解非齐次方程并不是很好使。

odeint+画图求数值解

这里我们用到求数值解的库叫做scipy；

scipy.odeint解数值解的思路是这样：

• 如果是二阶方程，需要化成两个一阶方程组成的方程组，如果是一阶则跳过该步骤；
• 把每个得到的方程组化成$y^{\prime }=f(x,y)$形式，这里的x和y是相对每个方程而言的，后面会详细讲；
• 因为要求的是数值解，所以需要确定好参数值和初始条件，在odeint中默认输入$y=0$的时因变量的值；
• 确定自变量范围并解方程，绘制图像；

下面还是看一个例子（scipy官网文档中的例子）：解微分方程 $y^{\prime \prime }+b\ast y^{\prime }+c\ast siny=0$，其中b，c是参数，对t求导；

按照上面的思路，首先化成两个一阶方程：
$$y^{\prime }(t)=z(t)\text{\hspace{1em}(1)}$$

$$z^{\prime }(t)=-b\ast z(t)-c\ast sin(y(t))\text{\hspace{1em}(2)}$$

上面的第二步中说的x和y是相对方程而言，拿方程（2）来讲就是将z‘(t)当作y’，z(t)当作y，t当作x，其他的当作参数，化为$y^{\prime }=f(x,y)$的形式，以便这个odeint解方程使用；

接下来看代码和注释，注释只解释基本方法：

import matplotlib.pyplot as plt
import scipy.integrate as sp
import numpy as np

#设定参数b，c初值，其实这个方程是物理学中跟钟摆重力角和摩擦力有关的一个微分方程
b = 0.25
c = 5.0

def function(t, y):#设定两个参数，约定第一个为自变量t，第二个为相对每个方程的因变量y
    yt, zt = y #规定每个方程的因变量
    return [zt, -b * zt - c * np.sin(yt)]#返回一个向量，每一项分别是每个方程的右半部分


t = np.linspace(0, 10, 100)#规定数值解的范围
init_x = [np.pi - 0.1, 0]#规定初值，传入的是一个向量，分别是每个方程的y=0时t的取值
result = sp.odeint(function, init_x, t, tfirst=True)#解方程，注意第一个参数只填函数名不要写括号，tfirst是指是否把求导自变量作为函数第一个参数

#画图部分
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

plt.xlabel('t')
plt.ylabel('f(t)')
plt.plot(t, result[:, 0], label='f:yt')#原函数数值解
plt.plot(t, result[:, 1], label='f:zt')#一阶导
plt.legend()
plt.show()

接下来我参考了一下说明文档，对代码中一些关键部分做一个详细的说明。

• 首先是我们的自定义函数，这个函数要作为odeint的必要参数，我们在调用odeint的时候，odeint会自动调用我们定义好的这个函数；
• 自定义函数的返回值是一个数组向量，第一项表示原函数（方程的解）一阶导的表示（这里我们用另一个符号zt表示），第二项就表示原函数二阶导表示（即上面的方程（2）），以此类推…
• 由于我们是求数值解，所以我们需要为每个方程规定一个初值，向量的第一项是第一个方程的初值，以此类推。在这里odeint默认初值为0，可以通过h0参数修改一下，详见https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html

得到的方程数值解可视化结果如下：

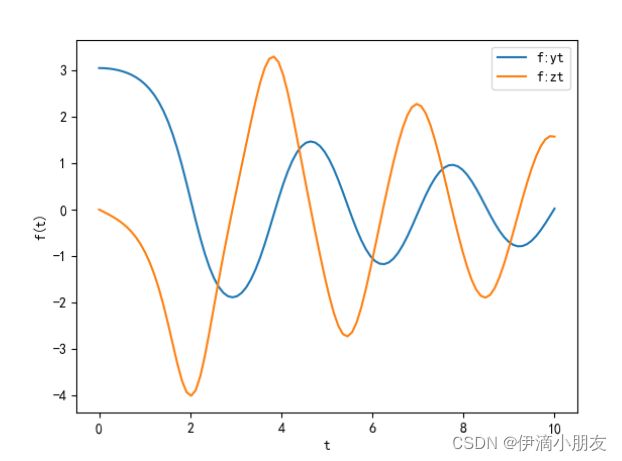
对照官网的答案可知是正确的。

求解微分方程组

一阶方程组求解

我们还是用dsolve来，整个过程跟解一个方程是差不多的，所以直接上例子：

我们还是用高数书上的例题来验证(357页)：

求微分方程组：
$$\{\begin{array}{l}{x}^{\prime }(t)=3\ast x(t)-2\ast y(t)\\ y^{\prime }(t)=2\ast z(t)-y(t)\end{array}$$
代码：

import sympy as sy

t = sy.symbols("t")
x = sy.Function("x")
y = sy.Function("y")

equation = x(t).diff(t,1)-3*x(t)+2*y(t)
equation2 = y(t).diff(t,1)-2*x(t)+y(t)

print(sy.dsolve([equation,equation2], [x(t),y(t)]))
sy.pprint(sy.dsolve([equation,equation2], [x(t),y(t)]))

只是多加了一个函数关系和一个方程，然后解方程的时候需要把两个方程和两个因变量写成一个数组传进对应的位置，依葫芦画瓢即可，最后得到的结果是这样的：

[Eq(x(t), (2*C1 + 2*C2*t + C2)*exp(t)), Eq(y(t), (2*C1 + 2*C2*t)*exp(t))]
⎡                             t                          t⎤
⎣x(t) = (2⋅C₁ + 2⋅C₂⋅t + C₂)⋅ℯ , y(t) = (2⋅C₁ + 2⋅C₂⋅t)⋅ℯ ⎦

跟书上答案有略微差别但是仔细看一下就会发现是等价的。

能解二阶方程组吗？

直接看高数书358页例题2：

import sympy as sy
from math import e

t = sy.symbols("t")
x = sy.Function("x")
y = sy.Function("y")

equation = x(t).diff(t,2)+y(t).diff(t,1)-x(t)-e**t
equation2 = y(t).diff(t,2)+x(t).diff(t,1)+y(t)

print(sy.dsolve([equation,equation2], [y(t),x(t)]))
sy.pprint(sy.dsolve([equation,equation2], [y(t),x(t)]))

发现这段代码会报错：

File "D:\Anaconda3\Anaconda\lib\site-packages\sympy\solvers\ode\ode.py", line 599, in dsolve
    raise NotImplementedError
NotImplementedError

它说没有实现hhh，翻看了一下ode.py文件，查看他能做到的求解微分方程的种类：

allhints = (
    "factorable",
    "nth_algebraic",
    "separable",
    "1st_exact",
    "1st_linear",
    "Bernoulli",
    "Riccati_special_minus2",
    "1st_homogeneous_coeff_best",
    "1st_homogeneous_coeff_subs_indep_div_dep",
    "1st_homogeneous_coeff_subs_dep_div_indep",
    "almost_linear",
    "linear_coefficients",
    "separable_reduced",
    "1st_power_series",
    "lie_group",
    "nth_linear_constant_coeff_homogeneous",
    "nth_linear_euler_eq_homogeneous",
    "nth_linear_constant_coeff_undetermined_coefficients",
    "nth_linear_euler_eq_nonhomogeneous_undetermined_coefficients",
    "nth_linear_constant_coeff_variation_of_parameters",
    "nth_linear_euler_eq_nonhomogeneous_variation_of_parameters",
    "Liouville",
    "2nd_linear_airy",
    "2nd_linear_bessel",
    "2nd_hypergeometric",
    "2nd_hypergeometric_Integral",
    "nth_order_reducible",
    "2nd_power_series_ordinary",
    "2nd_power_series_regular",
    "nth_algebraic_Integral",
    "separable_Integral",
    "1st_exact_Integral",
    "1st_linear_Integral",
    "Bernoulli_Integral",
    "1st_homogeneous_coeff_subs_indep_div_dep_Integral",
    "1st_homogeneous_coeff_subs_dep_div_indep_Integral",
    "almost_linear_Integral",
    "linear_coefficients_Integral",
    "separable_reduced_Integral",
    "nth_linear_constant_coeff_variation_of_parameters_Integral",
    "nth_linear_euler_eq_nonhomogeneous_variation_of_parameters_Integral",
    "Liouville_Integral",
       )

确实没有二阶常系数微分方程组这个类别，我的sympy是1.6.2版本的，不知道新版会不会增加这个功能。

总结：python解微分方程比较方便，可以满足绝大部分基础的需求（简单的数学建模方程基本都ok），如果需要更加高级的求解的话，建议转matlab。。。