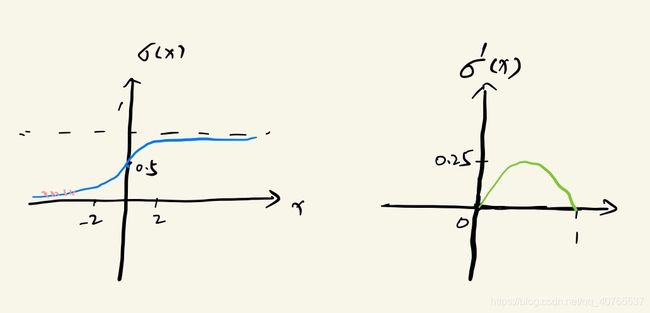机器学习: 神经网络中的Batch Normalization(BN)算法

一、什么是Batch Normalization

1. 从白化(Whiten)说起

    之前的研究表明如果在图像处理中对输入图像进行白化（Whiten）操作的话——所谓白化，就是对输入数据分布变换到0均值，单位方差的正态分布——那么神经网络会较快收敛。所以受白化启发，batch normalization被提出。

2. Batch Normalization

    接下来就看看什么是Batch Normalization。基于白化的思想，BN作者收到了启发，白化是在输入层对数据进行变换使其服从标准正态分布。对深度神经网络来说，其中某个隐层的输出就是下一层的输入，那么能不能对每个隐层都做白化呢？BN确实就是这么做的，并且在模型训练中取得了良好的效果。下面看一下BN算法的具体流程是怎样的。

    batch normaliztion算法伪代码

 

 (1).前三步

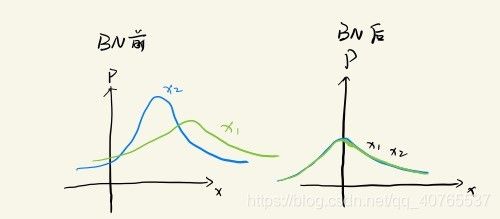
    我们知道前面三步把数据x的所有维度1..m的数据分布都变成了均值为0，方差为1的标准正态分布。下面以m=2为例，显示前三步的效果：

    

     

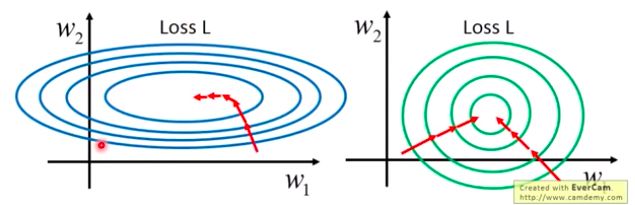
     这里第二幅图是L函数的等高线图。   ,  由于x被标准化了，所以关于w的L函数的几何表示是一个比较均衡的几何体。所以我们看到L函数在BN后会更加快地到达最优点，模型也更快收敛。

 (2).第四步

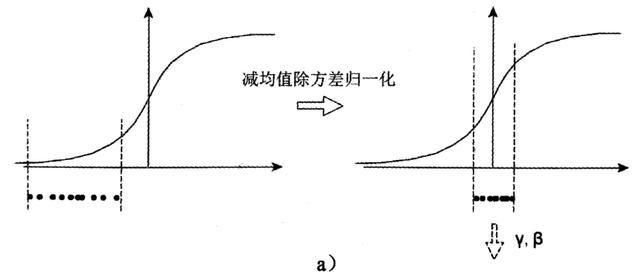
    这里值得注意的是最后一步缩放和移位。为什么需要进行缩放和移位呢？如果我们单单只进行前三步，假设我们使用sigmoid函数，那么x的分布情况是右边这样的：

   

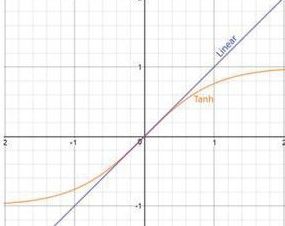
    所以如果只进行前三步，大部分的数据将会分布在Sigmoid函数的中间部分(线性区）。但是这样就没有达到用sigmoid函数对数据进行非线性变换的目的，换言之，减均值除方差操作后可能会削弱网络的性能。不光是Sigmoid激活函数，Tanh函数在零附近也变成线性，而Relu activation函数，则将一半的输入清零。

          

     所以我们需要对它进行缩放和移位。但是这里的缩放和移位是对各个维度进行同样的缩放和移位，所以不会使各个维度变得像原来一样地参差不齐。所以进行了四步的BN之后。同样假设我们使用sigmoid函数的话，x的分布情况是下面这样的：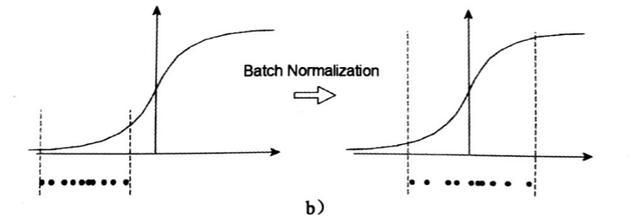 

 3. 在测试过程中的Batch Normalization

    当一个神经网络训练好后，我们就要拿来测试以及解决实际问题了。但是一个网络一旦训练完了，就没有了min-batch这个概念了，测试阶段我们一般只输入一个测试样本，再观察其结果。这个时候只有一个样本，我们就没有办法获取均值和方差，就没有办法进行测试。为了解决这个问题，该算法是利用训练集均值和方差来代替。假设训练过程中每个mini-batch的均值和方差为和。根据参数估计，我们求解出整个训练集的均值和方差为：

     

    所以最终它使用的公式是：

     

 二、Batch Normalization的作用

 1.加快收敛速度

    这点在前面都已经已经提到了，就是由于x被标准化了，所以关于w的L函数的几何表示是一个比较均衡的几何体, 在随机梯度下降过程中能更快地走到最优点。

    

2. 能够提高模型的精度

    这个也很好理解，同样利用上面1中的图，没有进行BN的话，我们得到扁平状的等高线，这样的话在训练后期，L极可能在最优点附近不断地进行小幅度的震荡而始终不能到达最优点。相比之下，右边的图梯度更明显，L能很快地直接到达最优点，从而使模型地精度提高。

3.能解决梯度消失问题

    其实这个是能够加快收敛速度的原因之一。也就是解决了梯度消失本身能加快收敛速度。

    下面看看它是怎么解决梯度消失问题的。假设没有经过BN调整前x的原先正态分布均值是-6，方差是1，那么意味着95%的值落在了[-8,-4]之间，那么对应的Sigmoid（x）函数的值明显接近于0，这是典型的梯度饱和区，在这个区域里梯度变化很慢，为什么是梯度饱和区？请看下sigmoid(x)如果取值接近0或者接近于1的时候对应导数函数取值，接近于0，意味着梯度变化很小甚至消失。关于梯度消失更多的内容可以参考：机器学习：神经网络中的梯度消失和梯度爆炸

    

4. 能提高模型的泛化能力 

    提高模型的泛化能力，换句话说，就是能够避免对训练集产生过拟合。这是因为在训练中，BN的使用使得一个mini-batch中的所有样本都被关联在了一起，因此网络不会从某一个训练样本中生成确定的结果。换句话说，就是同样一个样本的输出不再仅仅取决于样本本身，也取决于跟这个样本属于同一个mini-batch的其它样本。而泛化能力正是需要考虑大部分的样本，因而在考虑了大部分样本的影响之下，泛化能力自然提高。

    此外正因BN算法能够提高泛化能力，避免过拟合，我们就可以减少使用其他避免过拟合的方法(如L1， L2正则化项，Dropout)。详见：机器学习：正则化项为什么能够防止过拟合？防止过拟合的方法

三、参考资料

    【1】https://www.cnblogs.com/guoyaohua/p/8724433.html

    【2】https://www.jianshu.com/p/3da70e672c8b

    【3】https://baijiahao.baidu.com/s?id=1621528466443988599&wfr=spider&for=pc

    【4】https://blog.csdn.net/qq_29462849/article/details/83068421