高级UI强行进阶：自定义View实现女朋友欲罢不能的网易云音乐宇宙尘埃特效，拿去装笔不用谢~

前言

前段时间，女朋友用网易云音乐的时候看到一个宇宙尘埃特效，说很好看，想要让我给她开VIP用。

开什么玩笑？作为一个程序员为什么不能自己实现！开什么VIP！！

什么？女朋友？程序员有吗？我只在意特效的实现！

作者：Mlx
链接：https://juejin.im/post/6871049441546567688
高级UI进阶B站视频讲解：https://www.bilibili.com/video/BV1fE411P7PA

正文

0202年了，Android开发大都应该是老油条了把。如果你自定义View还是掌握得不够熟练的话，那可就说不过去了哦。自定义View可以说是Android开发中，无论是初级，中级还是高级都必须掌握的一个点。

不然的话，UI一不小心设计的太炫酷，那你岂不是要和他打起来了？难道你不想成为下图中的男人吗？

所以，自定义View的重要性已经不用我多说了。本篇是针对有自定义View基础知识，但是苦于没有好的项目模仿，或者说看到了酷炫效果没有思路不知道该如何下手的人。恭喜你，我将一步步手把手的带你分析效果，然后代码实现它。

我就知道没图是骗不到人的。先放图，大家看一下最终实现的效果。

ps：为了能更快加载出来，gif是压缩了又压缩，大家可以脑部清晰度。

ps2：小伙伴如果有好的gif压缩网站可以推荐一波

咳咳，虽然画质堪比AV画质，但是还是能看的出来效果是非常不错的。那么今天我就带小伙伴们一起从头到尾的实现一下这个效果吧。

特效分析

首先看动图，我们可以拆成两部分完成，一个是里面不断旋转的圆形图片，一个是外面不断扩散的粒子动效。

我们由易到难来完成，毕竟柿子要挑软的捏嘛。

另外由于本篇重点是讲自定义View的，所以就不采用ViewGroup的方式来实现图片和粒子动效的结合了。而是采用分开布局的方式。这样做的好处是可以只专注于粒子动效的实现，而不需要去考虑测量，布局等。

至于自定义ViewGroup，下一篇文章我将会带领大家实现一个非常非常非常酷炫的效果。

加载图片

我们先观察，首先这是一个圆形图片。其次，它在不停的转。

咳咳，先别骂，容我说完嘛。

圆形图片的话我们就用Glide来进行实现把，其实自定义View实现也可以，但我们重点还是粒子特效。

首先定义一个ImageView

现在我们去Activity中，用Glide加载一张圆形图片。

class DemoActivity : AppCompatActivity() {

    private lateinit var demoBinding: ActivityDemoBinding

    override fun onCreate(savedInstanceState: Bundle?) {
        super.onCreate(savedInstanceState)
        demoBinding = ActivityDemoBinding.inflate(layoutInflater)
        setContentView(demoBinding.root)

        lifecycleScope.launch(Dispatchers.Main) {
           loadImage()
        }
    }
    private suspend fun loadImage() {
        withContext(Dispatchers.IO) {
            Glide.with(this@DemoActivity)
                    .load(R.drawable.ic_music)
                    .circleCrop()
                    .into(object : ImageViewTarget(demoBinding.musicAvatar) {
                        override fun setResource(resource: Drawable?) {     
                            demoBinding.musicAvatar.setImageDrawable(resource)
                        }
                    })
        }
    }
}

这样我们利用Glide就加载了一个圆形的图片。

旋转图片

图片有了，接下来就应该是旋转了。

那么我们开始搞旋转。

旋转是如何实现的？我想不用我多说，很多小伙伴都知道，是动画嘛。

没错，就是动画。我们这里使用属性动画来实现。

定义一个属性动画并且给图片设置一个点击事件，让它旋转起来

lateinit var rotateAnimator: ObjectAnimator

override fun onCreate(savedInstanceState: Bundle?) {
        ...
        setContentView(demoBinding.root)
        rotateAnimator = ObjectAnimator.ofFloat(demoBinding.musicAvatar, View.ROTATION, 0f, 360f)
        rotateAnimator.duration = 6000
        rotateAnimator.repeatCount = -1
        rotateAnimator.interpolator = LinearInterpolator()
        lifecycleScope.launch(Dispatchers.Main) {
            loadImage()
            //添加点击事件，并且启动动画
            demoBinding.musicAvatar.setOnClickListener {
                rotateAnimator.start()
            }
        }
}

这些都是小儿科了，相信面对电视机前的观众朋友们，啊不，口误口误。

相信小伙伴们都很熟悉了，那我们开始今天的重头戏，这个粒子动画。

粒子动画

其实我很久以前看粒子动画的时候，也很好奇，这些炫酷的粒子动画是怎么实现的，当时的我完全没有思路。

尤其是看到一些图片，啪唧一下变成了一堆粒子，掉落，然后又呱唧从粒子变成了图片，就觉得异常的牛X。

其实啊，一点都不神奇。

首先我们要知道bitmap是什么。bitmap是什么呀？

在数学上，有这么几个概念，点，线，面。点很好理解，就是一个点。线是由一堆点组成的，而面又类似于一堆线组成的。本质上，面就是由无数的点组成的。

可是这和bitmap以及今天的粒子动画有什么关系呢？

一个bitmap，我们可以简单地理解为一张图片。这个图片是不是一个平面呢？而平面又是一堆点组成的，这个点在这里称为像素点。所以bitmap就是由一堆像素点所组成的，有趣的是，这些像素点是有颜色的，当这些像素点足够小，你离得足够远你看起来就像一幅完整的画了。

在现实中也不乏这样的例子，举办一些活动的时候，一个个人穿着不同颜色的衣服有序的站在广场上，如果有一架无人机在空中看，就能看到是一幅画。就像这样

所以当把一幅画拆成一堆粒子的话，其实就是获得bitmap中所有的像素点，然后改变他们的位置就可以了。如果想要用一堆粒子拼凑出一幅画，只需要知道这些粒子的顺序，排放整齐自然就是一幅画了。

扯远了，说这些呢其实和今天的效果没有特别强的联系，只是为了让你能够更好的理解粒子动画的本质。

粒子动画分析

我们先观察这个特效，你会发现有一个圆，这个圆上不断的往外发散粒子，粒子在发散的过程中速度是不相同的。而且，在发散的过程中，透明度也在不断变化，直到最后完全透明。

好，我们归纳一下。

• 圆形生产粒子
• 粒子速度不同，也就是随机。
• 粒子透明度不断降低，直到最后消散。
• 粒子沿着到圆心的反方向扩散。

写自定义View的时候千万不要一上来就开干，而是要逐渐分析，有的时候我们遇到一个复杂的效果，更是要逐帧的分析。

而且我写自定义View的时候有个习惯，就是一点点的实现效果，不会去一次性实现全部的效果。

所以我们第一步，生产粒子。

生产粒子

首先，我们可以知道，粒子是有颜色的，但是似乎这个效果粒子只有白色，那就指定粒子颜色为白色了。

然后我们可以得出，粒子是有位置的，位置肯定由x，y组成嘛。然后粒子还有个速度，以及透明度和半径。

定义粒子

我们可以定义一个粒子类：

class Particle(
    var x:Float,//X坐标
    var y:Float,//Y坐标
    var radius:Float,//半径
    var speed:Float,//速度
    var alpha: Int//透明度
)

由于我们的这个效果看起来就像是水波一样的涟漪，我给自定义View起名为涟漪，也就是dimple

我们来定义这个自定义View把

定义自定义view

class DimpleView(context: Context?, attrs: AttributeSet?) : View(context, attrs) {
    //定义一个粒子的集合  
    private var particleList = mutableListOf()
    //定义画笔
    var paint = Paint()
}

一开始就直接圆形生产粒子着实有些难度，我先考虑考虑如何实现生产粒子把。

先不断生产粒子，然后再考虑圆形的事情。

而且生产一堆粒子比较麻烦，我先实现从上到下生产一个粒子。

那么如何生产一个粒子呢？前面也说了，粒子就是个很小的点，所以用canvas的drawCircle就可以。

那我们来吧

override fun onDraw(canvas: Canvas) {
        super.onDraw(canvas)
        paint.color = Color.WHITE
        paint.isAntiAlias = true
        var particle=Particle(0f,0f,2f,2f,100)
        canvas.drawCircle(particle.x, particle.y, particle.radius, paint)
}

画画嘛，就要在onDraw方法中进行了。我们先new一个Particle，然后画出来。

实际上这样并没有什么效果。为啥呢？

我们的背景是白色的，粒子默认是白色的，你当然看不到了。所以我们需要先做个测试，为了能看出效果。这里啊，我们把背景换成黑色。同时，为了方便测试，先把Imageview设置成不可见。然后我们看下效果

没错，就是没什么效果。你什么都看不出来。

先不急，慢慢来，且听我吹，啊不，且听我和你慢慢道来。

我们在这里只花了一个圆，而且是在坐标原点画了一个半径为2的点，可以说很小很小了。自然就看不到了。

什么，你不知道原点在哪？

棕色部分就是我们的屏幕，所以原点就是左上角。

现在我们需要做的事情只有两个，要么把点变大，要么改变点的位置。

粒子粒子的，当然不能变大，所以我们把它放到屏幕中心去。

所以我们定义一个屏幕中心的坐标，centerX,centerY。并且在onSizeChanged方法中给它们赋值

override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
        super.onSizeChanged(w, h, oldw, oldh)
        centerX= (w/2).toFloat()
        centerY= (h/2).toFloat()
}

那我们改一下上面的画点的代码：

override fun onDraw(canvas: Canvas) {
        ...
        var particle=Particle(centerX,centerY,2f,2f,100)
        canvas.drawCircle(particle.x, particle.y, particle.radius, paint)
}

如此，可以看到这个点了，虽然很小很小，但是也胜过没有呀

可是这时候有人跳出来了，说你这不对啊，一个点有啥用？还那么小，我本来就近视，你这搞得我更看不清了。你是不是眼睛店派来的叛徒！

添加多个粒子

那好吧，我们多加几个。可是该怎么加？效果图中是圆形的，可是我不会啊，我只能先试试一横排添加。看看这样可不可以呢？我们知道，横排的话就是y值不变，x变。好，但是为了避免我们画出一条线，我们x值随机增加，这样的话看起来也比较不规则一些。

那么代码就应该是这样了

override fun onDraw(canvas: Canvas) {
        super.onDraw(canvas)
        paint.color = Color.WHITE
        paint.isAntiAlias = true
        for (i in 0..50){
            var random= Random()
            var nextX=random.nextInt((centerX*2).toInt())
            var particle=Particle(nextX.toFloat(),centerY,2f,2f,100)
            canvas.drawCircle(particle.x, particle.y, particle.radius, paint)
        }

}

由于centerX是屏幕的中心，所以它的值是屏幕宽度的一半，这里的话X的值就是在屏幕宽度内随机选一个值。那么效果看起来是下面这样

效果看起来不错了。

但是总有爱搞事的小伙伴又跳出来了，说你会不会写代码？onDraw方法一直被调用，不能定义对象你不知道么？很容易引发频繁的GC，造成内存抖动的。而且你这还搞个循环，性能能行不？

这个小伙伴你说的非常对，是我错了！

确实，在ondraw方法中不适合定义对象，尤其是for循环中就更不能了。段时间看，我们50个粒子好像对性能的开销不是很大，但是一旦粒子数量很多，性能开销就会十分的大。而且，为了不掉帧，我们需要在16ms之内完成绘制。这个不明白的话我后续会有性能优化的专题，可以关注一下我~

这里我们测量一下50个粒子的绘制时间和5000个粒子的绘制时间。

override fun onDraw(canvas: Canvas) {
        super.onDraw(canvas)
        paint.color = Color.WHITE
        paint.isAntiAlias = true
        var time= measureTimeMillis {
            for (i in 0..50){
                var random= Random()
                var nextX=random.nextInt((centerX*2).toInt())
                var particle=Particle(nextX.toFloat(),centerY,2f,2f,100)
                canvas.drawCircle(particle.x, particle.y, particle.radius, paint)
            }
        }
        Log.i("dimple","绘制时间$time ms")
}

结果如下：50个粒子的绘制时间

5000个粒子的绘制时间：

可以看到，明显超了16ms。所以我们需要优化，怎么优化？很简单，就是不在ondraw方法中创建对象就好了，那我们选择在哪里呢？

构造方法可以吗？好像不可以呢，这个时候还没办法获得屏幕宽高，嘿嘿嘿，onSizeChanged方法就决定是你了！

粒子添加到集合中

override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
        super.onSizeChanged(w, h, oldw, oldh)
        centerX= (w/2).toFloat()
        centerY= (h/2).toFloat()
        val random= Random()
        var nextX=0
        for (i in 0..5000){
            nextX=random.nextInt((centerX*2).toInt())
            particleList.add(Particle(nextX.toFloat(),centerY,2f,2f,100))
        }
}

我们再来看看onDraw方法中绘制时间是多少：

override fun onDraw(canvas: Canvas) {
    super.onDraw(canvas)
    paint.color = Color.WHITE
    paint.isAntiAlias = true
    var time= measureTimeMillis {
        particleList.forEach {
            canvas.drawCircle(it.x,it.y,it.radius,paint)
        }
    }
    Log.i("dimple","绘制时间$time ms")
}

emmmm,好像是低于16ms了，可是这也太危险了吧，你这分分钟就超过了16ms啊。

确实是这样子，但是实际情况下，我们并不需要5000个这么多的粒子。又有人问，，万一真的需要怎么办？那就得看surfaceView了。这里就不讲了

我们还是回过头来，先把粒子数量变成50个。

现在粒子也有了，该实现动起来的效果了。

动起来，我们想想，应该怎么做呢？效果图是类似圆一样的扩散，我现在做不到，我往下掉这应该不难吧？

说动就动，搞起！至于怎么动，那肯定是属性动画呀。

定义动画

private var animator = ValueAnimator.ofFloat(0f, 1f)
init {
        animator.duration = 2000
        animator.repeatCount = -1
        animator.interpolator = LinearInterpolator()
        animator.addUpdateListener {
            updateParticle(it.animatedValue as Float)
            invalidate()//重绘界面
        }
}

我在这里啊，定义了一个方法updateParticle，每次动画更新的时候啊就去更新粒子的状态。

updateParticle方法应该去做什么事情呢？我们来开动小脑筋想想。

如果说是粒子不断往下掉的话，那应该是y值不断地增加就可以了，嗯，非常有道理。

我们来实现一下这个方法

更新粒子位置

private fun updateParticle(value: Float) {
    particleList.forEach {
        it.y += it.speed
    }
}
override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
        ...
        animator.start()//别忘了启动动画
    }

那我们现在来看一下效果如何

emmmm看起来有点雏形了，不过效果图里的粒子速度似乎是随机的，咱们这里是同步的呀。

没关系，我们可以让粒子的速度变成随机的速度。我们修改添加粒子这里的代码

override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
        super.onSizeChanged(w, h, oldw, oldh)
        centerX = (w / 2).toFloat()
        centerY = (h / 2).toFloat()
        val random = Random()
        var nextX = 0
        var speed=0 //定义一个速度
        for (i in 0..50) {
            nextX = random.nextInt((centerX * 2).toInt())
            speed= random.nextInt(10)+5 //速度从5-15不等
            particleList.add(
                Particle(nextX.toFloat(), centerY, 2f, speed.toFloat(), 100)
            )
        }
        animator.start()
    }

这是效果，看起来有点样子了。不过问题又来了，人家的粒子是一直散发的，你这个粒子怎么没了就是没了呢？

有道理，所以我觉得我们需要设置一个粒子移动的最大距离，一旦超出这个最大距离，我们啊就让它回到初始的位置。

修改粒子的定义

class Particle(
    var x:Float,//X坐标
    var y:Float,//Y坐标
    var radius:Float,//半径
    var speed:Float,//速度
    var alpha: Int, //透明度
    var maxOffset:Float=300f//最大移动距离
)

如上，我们添加了一个最大移动距离。但是有时候我们往往最大移动距离都是固定的，所以我们这里给设置了一个默认值，如果哪个粒子想特立独行也不是不可以。

有了最大的移动距离，我们就得判定，一旦移动的距离超过了这个值，我们就让它回到起点。这个判定在哪里做呢？当然是在更新位置的地方啦

粒子运动距离判定

private fun updateParticle(value: Float) {
        particleList.forEach {
            if(it.y - centerY >it.maxOffset){
                it.y=centerY //重新设置Y值
                it.x = random.nextInt((centerX * 2).toInt()).toFloat() //随机设置X值
                it.speed= (random.nextInt(10)+5).toFloat() //随机设置速度
            }
            it.y += it.speed
        }
}

本来呀，我想慢慢来，先随机Y，在随机X和速度。

但是我觉得可以放在一起讲，因为一个粒子一旦超出这个最大距离，那么它就相当于被回收重新生成一个新的粒子了，而一个新的粒子，必然X，Y，速度都是重新生成的，这样才能看起来效果不错。

那我们运行起来看看效果把。

emmm似乎还不错的样子？不过人家的粒子看起来很多呀，没关系，我们这里设置成300个粒子再试试？

看起来已经不错了。那我们接下来该怎么办呢？是不是还有个透明度没搞呀。

透明度的话，我们想想该如何去设置呢？首先，应该是越远越透明，直到最大值，完全透明。这就是了，透明度和移动距离是息息相关的。

粒子移动透明

private fun updateParticle(value: Float) {
        particleList.forEach {
            ...
            //设置粒子的透明度
            it.alpha= ((1f - (it.y-centerY) / it.maxOffset)  * 225f).toInt()
            ...
        }
}
override fun onDraw(canvas: Canvas) {
        ...
        var time = measureTimeMillis {
            particleList.forEach {
                //设置画笔的透明度
                paint.alpha=it.alpha
                canvas.drawCircle(it.x, it.y, it.radius, paint)
            }
        }
        ...
}

再看一下效果。。。

看起来不错了，有点意思了哦~~不过好像不够密集，我们把粒子数量调整到500就会好很多哟。而且，不知道大家有没有发现在动画刚刚加载的时候，那个效果是很不好的。因为所有的例子起始点是一样的，速度也难免会有一样的，所以效果不是很好，只需要在添加粒子的时候，Y值也初始化即可。

override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
    super.onSizeChanged(w, h, oldw, oldh)
    ...
    var nextY=0f
    for (i in 0..500) {
        ...
        //初始化Y值，这里是以起始点作为最低值，最大距离作为最大值
        nextY= random.nextInt(400)+centerY
        speed= random.nextInt(10)+5
        particleList.add(
            Particle(nextX.toFloat(), nextY, 2f, speed.toFloat(), 100)
        )
    }
    animator.start()
}

这样一来，效果就会很好了，没有一点问题了。现在看来，似乎除了不是圆形以外，没有什么太大的问题了。那我们下一步就该思考如何让它变成圆形那样生成粒子呢？

定义圆形

首先这个圆形是圆，但又不能画出来。

什么意思？

就是说，虽然是圆形生成粒子，但是不能够画出来这个圆，所以这个圆只是个路径而已。

路径是什么？没错，就是Path。

熟悉的小伙伴们就知道，Path可以添加各种各样的路径，由圆，线，曲线等。所以我们这里就需要一个圆的路径。

定义一个Path，添加圆。注意，我们上面讲的性能优化，不要再onDraw中定义哦。

var path = Path()
override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
    ...
    path.addCircle(centerX, centerY, 280f, Path.Direction.CCW)
    ...
}

在onSizeChanged中我们添加了一个圆，参数的意思我就不讲了，小伙伴应该都明白。

现在我们已经定义了这个Path，但是我们又不画，那我们该怎么办呢？

我们思考一下，我们如果想要圆形生产粒子的话，是不是得需要这个圆上的任意一点的X,Y值有了这个X,Y值，我们才能够将粒子的初始位置给确定呢？看看有没人有知道怎么确定位置啊，知道的小伙伴举手示意一下

啊，等了十几分钟也没见有小伙伴举手，看来是没人了。

好汉饶命！

我说，我说，其实就是PathMeasure这个类，它可以帮助我们得到在这个路径上任意一点的位置和方向。不会用的小伙伴赶紧谷歌一下用法吧~或者看我代码也很好理解的。

private val pathMeasure = PathMeasure()//路径，用于测量扩散圆某一处的X,Y值
private var pos = FloatArray(2) //扩散圆上某一点的x,y
private val tan = FloatArray(2)//扩散圆上某一点切线

这里我们定义了三个变量，首当其冲的就是PathMeasure类，第二个和第三个变量是一个float数组，pos是用来保存圆上某一点的位置信息的，其中pos[0]是X值，pos[1]是Y值。

第二个变量tan是某一点的切线值，你可以暂且理解为是某一点的角度。不过我们这个效果用不到，只是个凑参数的。

PathMeasure有个很重要的方法就是getPosTan方法。

boolean getPosTan (float distance, float[] pos, float[] tan)

方法各个参数释义：

参数	作用	备注
返回值(boolean)	判断获取是否成功	true表示成功，数据会存入 pos 和 tan 中， false 表示失败，pos 和 tan 不会改变
distance	距离 Path 起点的长度	取值范围: 0 <= distance <= getLength
pos	该点的坐标值	当前点在画布上的位置，有两个数值，分别为x，y坐标。
tan	该点的正切值	当前点在曲线上的方向，使用 Math.atan2(tan[1], tan[0]) 获取到正切角的弧度值。

相信小伙伴还是能看明白的，我这里就不一一解释了。

所以到了这里，我们已经能够获取圆上某一点的位置了。还记得我们之前是怎么设置初始位置的吗？就是Y值固定，X值随机，现在我们已经能够得到一个标准的圆的位置了。但是，很重要啊，但是如果我们按照圆的标准位置去一个个放粒子的话，岂不就是一个圆了？而我们的效果图，位置可看起来不怎么规律。

所以我们在得到一个标准的位置之后，需要对它进行一个随机的偏移，偏移的也不能太大，否则成不了一个圆形。

圆形添加粒子

所以我们要修改添加粒子的代码了。

override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
        super.onSizeChanged(w, h, oldw, oldh)
        centerX = (w / 2).toFloat()
        centerY = (h / 2).toFloat()
        path.addCircle(centerX, centerY, 280f, Path.Direction.CCW)
        pathMeasure.setPath(path, false) //添加path
        var nextX = 0f
        var speed=0
        var nextY=0f
        for (i in 0..500) {
            //按比例测量路径上每一点的值
            pathMeasure.getPosTan(i / 500f * pathMeasure.length, pos, tan)
            nextX = pos[0]+random.nextInt(6) - 3f //X值随机偏移
            nextY=  pos[1]+random.nextInt(6) - 3f//Y值随机偏移
            speed= random.nextInt(10)+5
            particleList.add(
                Particle(nextX, nextY, 2f, speed.toFloat(), 100)
            )
        }
        animator.start()
    }

现在运行起来就是这样子了

咦，效果和我想象的不一样啊。最初好像是个圆，可是不是应该像涟漪一样扩散吗，可你这还是往下落呀。

还记得我们之前定义的动画的效果吗，就是X值不变，Y值不断扩大，那可不就是一直往下落吗？所以这里我们需要修改动画规则。

修改动画

问题是怎么修改动画呢？

思考一下，效果图中的动画应该是往外扩散，扩散是什么意思？就是沿着它到圆心的方向反向运动，对不对？

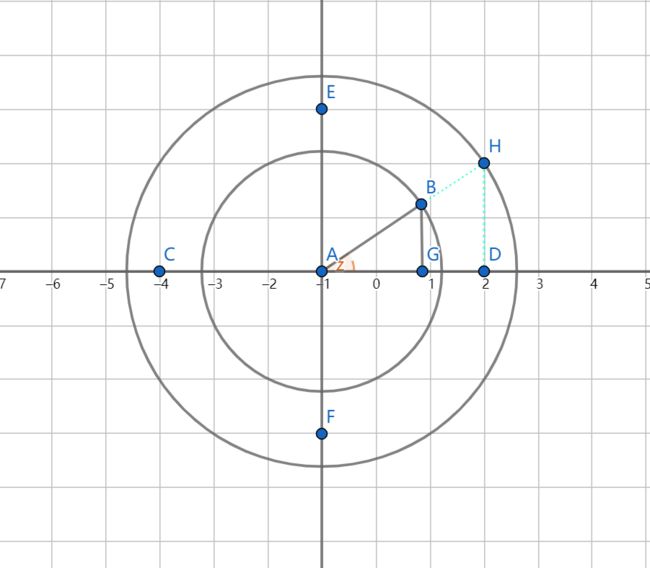
上一张图来理解一下

此时内心圆是我们现在粒子所处的圆，假设有一个粒子此时在B点，那么如果要扩散的话，它应该到H点位置。

这个H点的位置应该如何获取呢？

如果以A点为原点的话，此时B点的位置我们是知道的，它分别是X和Y。X=AG，Y=BG。我们也应该能发现，由AB延申至AH的过程中，∠Z是始终不变的。

同时我们应该能发现，扩散这个过程实际上是圆变大了，所以B变挪到了H点上。而这个扩大的值的意思就是圆的半径变大了，即半径R = AB，现在半径R=AH。

AB的值我们是知道的，就是我们一开始画的圆的半径嘛。可是AH是多少呢？

不妨令移动距离offset=AH-AB，那么这个运动距离offset是多少呢？我们想一下，在之前的下落中，距离是不是等于速度乘以时间呢？而我们这里没有时间这个变量，有的只是一次次循环，循环中粒子的Y值不断加速度。所以我们需要一个变量offset值来记录移动的距离，

所以这个offset += speed

那我们现在offset知道了，也就是说AH-AB的值知道了，AB我们也知道，我们就能求出AH的值

AH=AB +offset

AH知道了，∠Z也知道了，利用三角函数我们可以得到H点的坐标了。设初始半径为R=AB

A点为原点，

cos(∠Z)=AG/AB，sin(∠Z)=BG/AB

所以AD

AD=AH∗cos(∠Z)=(AH∗AG)/AB=((R+offset)∗AG)/R

HD

HD=AH∗sin(∠Z)=(AH∗BG)/AB=((R+offset)∗BG)/R

按理说没问题了，这个时候H的值我们已经得到了。但是，注意此时我们是以A点为原点得出来的值，而我们的手机屏幕中是以左上角为原点的。A点的值我们此时在程序中写死了是centerX和centerY，所以上面的公式还得改一下

AD=((R+offset)∗(B.X−centerX))/R

HD=((R+offset)∗(centerY−B.Y))/R

注意哦，此时只是AD和HD的值，只是这两个线段的长度而不是真正H点的坐标。H点的坐标应该在A点的基础上增加，即

H.X=AD+centerX=((R+offset)∗(B.X−centerX))/R+centerX

H.Y=centerY−HD=centerY−((R+offset)∗(centerY−B.Y))/R

而且这只是在右上半区也就是第一象限是这样计算的，左半区和右下半区的计算规则也不一样。

兄台，不要急，先听我说，一会还不懂的话我亲自帮你踢板凳。

小伙伴纷纷表示，上边的公式也太复杂了，每个象限都计算一遍，自定义View就这么复杂吗？

哈哈哈哈，其实不是。我晃点你的。

规则也确实是上面所说的，但是我们是什么人？程序员啊，最不应该怕的就是计算了。反正CPU算不是我算。

我们在分析一遍，这次一定很简单，你不要跑！

首先有个角度Z，我们需要记下每个粒子的角度，可是这个角度的计算就有的说道了。

我们先以左右两个半区计算，在右半区的时候角度

Z=(B.X−centerX)/R

假设这个时候∠Z是30°，那么也就是说

cos∠Z=0.5

那么H的X值也就是

H.X=AH∗0.5+centerX

可是如果在左半区的话角度Z

cos∠Z=−0.5

那么此时H的X值应该是这么算

H.X=centerX−AH∗0.5

其实本质上

H.X=centerX+AH∗cos∠Z

我们根本不需要考虑左右的问题，因为如果在右边cos∠Z是正，在左边为负数，所以直接加就可以。

而我们需要考虑的是上下问题，也就是Y的问题。毕竟这个正负是基于X的值算出来的。当我们转换成角度以后需要根据此时H的Y值是否大于centerY来分别计算。

当H的Y值在centerY之上，也就是H.Y

H.Y=centerY−AH∗abs(sin∠Z)

反之

H.Y=centerY+AH∗abs(sin∠Z)

这样的话随着offset的增长，H点的坐标也能够随时的计算出来了。

话说再多也没用，还是代码更为直观。

根据上面的描述，我们需要给粒子添加两个属性，一个是移动距离，一个是粒子的角度

class Particle(
    ...
    var offset:Int,//当前移动距离
    var angle:Double,//粒子角度
    ...
)

在添加粒子的地方修改：

override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
    ...
    var angle=0.0
    for (i in 0..500) {
        ...
        //反余弦函数可以得到角度值，是弧度
        angle=acos(((pos[0] - centerX) / 280f).toDouble())
        speed= random.nextInt(10)+5
        particleList.add(
            Particle(nextX, nextY, 2f, speed.toFloat(), 100,0,angle)
        )
    }
    animator.start()
}

在更新粒子动画的地方修改：

private fun updateParticle(value: Float) {
    particleList.forEach {particle->
        if(particle.offset >particle.maxOffset){
            particle.offset=0
            particle.speed= (random.nextInt(10)+5).toFloat()
        }
        particle.alpha= ((1f - particle.offset / particle.maxOffset)  * 225f).toInt()
        particle.x = (centerX+ cos(particle.angle) * (280f + particle.offset)).toFloat()
        if (particle.y > centerY) {
            particle.y = (sin(particle.angle) * (280f + particle.offset) + centerY).toFloat()
        } else {
            particle.y = (centerY - sin(particle.angle) * (280f + particle.offset)).toFloat()
        }
        particle.offset += particle.speed.toInt()
    }
}

添加粒子的地方angle是角度值，用了Kotlin的acos反余弦函数，这个函数返回的是0-PI的弧度制，0-PI的取值范围也就意味着sin∠Z始终是正值，上面公式中的绝对值就不需要了。

更新的代码很简单，对照公式一看便知。此时我们运行一下，效果就已经很好了，很接近了。

现在感觉是不是好多了？就是速度有点快，粒子有点少~没关系，我们做一些优化工作，比如说，粒子的初始移动距离也随机取一个值，粒子的最大距离也随机。这样下来，我们的效果就十分的好了

override fun onSizeChanged(w: Int, h: Int, oldw: Int, oldh: Int) {
    super.onSizeChanged(w, h, oldw, oldh)
    centerX = (w / 2).toFloat()
    centerY = (h / 2).toFloat()
    path.addCircle(centerX, centerY, 280f, Path.Direction.CCW)
    pathMeasure.setPath(path, false)
    var nextX = 0f
    var speed=0f
    var nextY=0f
    var angle=0.0
    var offSet=0
    var maxOffset=0
    for (i in 0..2000) {
        pathMeasure.getPosTan(i / 2000f * pathMeasure.length, pos, tan)
        nextX = pos[0]+random.nextInt(6) - 3f
        nextY=  pos[1]+random.nextInt(6) - 3f
        angle=acos(((pos[0] - centerX) / 280f).toDouble())
        speed= random.nextInt(2) + 2f
        offSet = random.nextInt(200)
        maxOffset = random.nextInt(200)
        particleList.add(
            Particle(nextX, nextY, 2f, speed, 100,offSet.toFloat(),angle, maxOffset.toFloat())
        )
    }
    animator.start()
}

其实还有很多可以优化的地方，比如说，粒子的数量抽取为一个常量，中间圆的半径也可以定为一个属性值去手动设置等等。。不过这些都是小意思，相信小伙伴们一定可以自己搞定的。我就不班门弄斧了。

最后这是优化过后的效果，接下来的与图片结合，就希望小伙伴们自己实现一下啦~很简单的。可以在评论区交作业哦

这是我的成品地址，做了一些额外的优化，比如说x和y的随机偏移等。小伙伴们可以手动去实现一下或者看我代码，当然我代码只是为了实现效果，并没有做更多的优化，不要喷我哦：DimpleView

预告

这一次是自定义View。 下一次我将要带大家实现自定义ViewGroup，效果是这样的，是不是更加炫酷？欢迎关注我，一个喜欢自定义View和NDK开发的小喵喵~

觉得文章有点意思的话，不妨点个赞再走呀，啊呜~