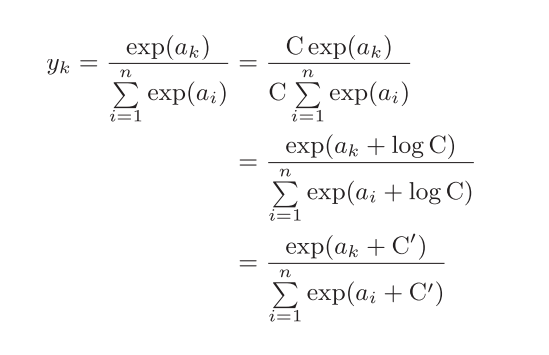动手实现深度神经网络1 两层神经网络
动手实现深度神经网络1 两层神经网络
在这个系列中,我们将尝试使用python手写一个神经网络,当然实际可用的神经网络模型非非常复杂,涉及诸多实现细节和优化,因此,我们先从一个两层的神经网络开始,之后不断完善和改进。
我们使用这个网络进行MNIST数据集手写数字识别,因为这是第一个网络,所以事先比较简单,没有实现批处理等,而是每次输入一个图片(MNIST数据集中的一个手写图片时28*28的矩阵,为了运算方便,我们一般把它扁平化为有784个元素的一维矩阵)。同时,因为在计算梯度时采用数值微分的方法,这样是非常慢的,因此训练数据和测试数据都只能从MNIST数据集中选取一小部分。不过不要灰心,等到下一篇文章时,就会实现一个快速高效的神经网络了。
1.网络的基本结构
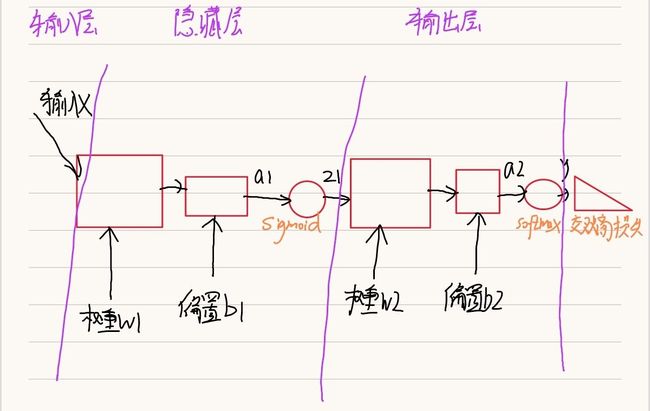
2.两层神经网络的类
2.1定义类与类初始化函数
class Myself_Two_Layer_Net:
# 一个神经网络在初始化应该接受一些超参数的设定如:各层神经元数量、初始化参数时的高斯分布的规模
def __init__(self,input_size,hidden_size,output_size,weight_init_std):
# 这是神经网络的参数,使用字典存放
# 参数初始化
self.params={}
# w1 b1是第一层(隐藏层)的权重和偏置
# w1的形状是input_size*hidden_size的矩阵 b1的形状是有hidden_size格元素的一维矩阵 图
# 参数一般初始化时选用高斯分布(正态分布)随机数 np.random.randn(a,b)生成a行b列的符合高斯分布的随机数矩阵
self.params['w1']=weight_init_std*np.random.randn(input_size,hidden_size)
self.params['b1']=hidden_size
# w2 b2是第二层(隐藏层)的权重和偏置
self.params['w2'] = weight_init_std * np.random.randn(hidden_size,output_size)
self.params['b2'] = output_size
一个神经网络在初始化应该接受一些超参数的设定如:各层神经元数量、参数初始化规则等。因为“根据梯度调整参数”的工作没有放在这个类中,所以不需要接受学习率。
参数初始化一般使用高斯分布随机初始化。关于各层神经元数量的具体值,等到后面使用这个网络时再说明。
2.2两层神经网络的工作流程
1 接收输入–>2 经过两层运算–>3 求损失函数值–>4 求个损失函数值关于各个参数的梯度–>5 (根据梯度更新参数)
步骤1已经在“类初始化方法”中实现了,步骤5由类的使用者实现。因此主要是实现2 3 4三个步骤。
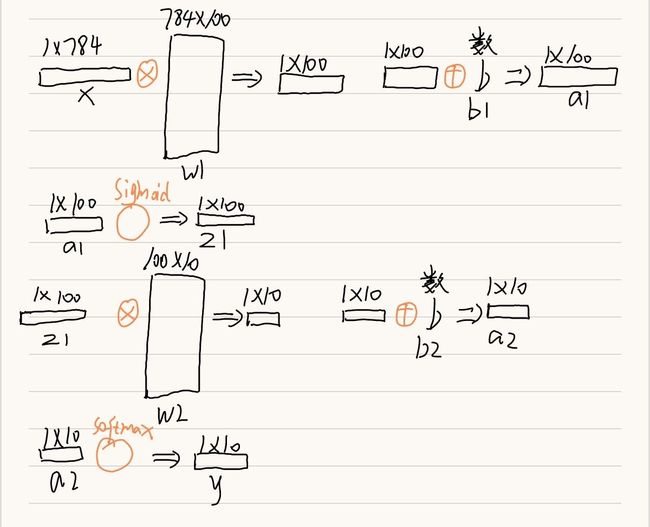
2.2.1经过两层运算
# 经过两层运算
def predict(self,x):
# 取出参数
w1,b1=self.params['w1'],self.params['b1']
w2,b2=self.params['w2'],self.params['b2']
a1=np.dot(x,w1)+b1
# 这里需要我们自己实现一下sigmoid激活函数
z1=sigmoid(a1)
a2=np.dot(z1,w2)+b2
# 这里需要我们自己实现一下softmax激活函数
y=softmax(a2)
return y
可以看到,神经网络的计算流程还是很简单的。我们使用np.dot进行矩阵乘法。
这里需要我们自己实现一下sigmoid和softmax两个激活函数(如果对于这两个激活函数还不熟悉,可以看我之前的文章,有详细的讲解)
def sigmoid(x):
# 因为是矩阵运算所以使用np.exp而不是math.exp
return 1/(1+np.exp(-x))
def softmax(x):
max=np.max(x)
x=x-max
return np.exp(x)/np.sum(np.exp(x))
(这里的softmax函数只是用与没有实现批处理的神经网络,在后续文章中会对它进行过完善)
max=np.max(x)
x=x-max
这两行代码是防止计算溢出,这里回答两个问题:
1.为什么会出现计算溢出?
因为softmax函数的实现中要进行指数函数的运算,但是指数函数的值很容易变得非常大。比如,exp(10)的值 会超过20000,exp(100)会变成一个后面有40多个0的超大值,exp(1000)的结果会返回 一个表示无穷大的inf。如果在这些超大值之间进行除法运算,结果会出现“不确定”的情况。
2.为什么会可以使用减去最大值这样简单粗暴的函数?
从这个式子中可以看出在进行softmax的指数函数的运算时,加上(或者减去) 某个常数并不会改变运算的结果。
2.2.2求损失函数值
# 求损失函数值
def loss(self,x,t):
y=self.predict(x)
# 这里需要我们自己实现一下交叉熵损失函数
return cross_entropy_error(y,t)
# 无batch学习的交叉熵函数 监督数据是one-hot格式
# 对于监督数据是one-hot格式的情况 实际上只计算对应正确解标签的输出的自然对数
def cross_entropy_error(y,t):
# 函数内部在计算np.log时,加上了一个微小值delta 1e-7。
# 这是因为,当出现np.log(0)时,np.log(0)会变为负无限大的 - inf,这样一来就会导致后续计算无法进行。作为保护性对策,添加一个微小值可以防止负无限大的发生
delta=1e-7
return -np.sum(t*np.log(y+delta))
这里解释两个问题:
一个是监督数据。它很容易个测试数据这个概念混淆起来,后面的代码会让你有一个更直观的认识

一个是one-hot格式(独热编码),它指的是将正确解标签设为1,其他均设为0
假设监督数据t是[0,0,1,0,0,0,0,0,0,0] 神经网络的输出y是[0.1,0.05,0.6,0.1…] 正确解标签的索引是“2”,与之对应的神经网络的输出是0.6
那么交叉熵就是:就是−log 0.6 = 0.51
我们写一个例子验证一下:
t=np.array([0,0,1,0,0,0,0,0,0,0])
# 这里关键是索引2上是0.6 其他位置数据都不重要
y=np.array([0.1,0.05,0.6,0.05,0.05,0.05,0.01,0.01,0.02,0.06])
print(np.log(y))
print(t*np.log(y))
z=-np.sum(t*np.log(y))
print(z)
因此,可以说交叉熵误差的值是由正确解标签所对应的输出结果决定的。
2.2.3求个损失函数值关于各个参数的梯度
# 求个损失函数值关于各个参数的梯度
def gradient_numerical(self,x,t):
# 将前面两步运算构成lambda表达式(可以理解为数学上的一个函数)传递给计算梯度的的方法
loss_W=lambda w:self.loss(x,t)
grads={}
# 这里需要我们自己实现一下numerical_gradient(用数值微分发计算梯度)
grads['w1'] = numerical_gradient_2d(loss_W, self.params['w1'])
grads['b1'] = numerical_gradient_onenumber(loss_W, self.params['b1'])
grads['w2'] = numerical_gradient_2d(loss_W, self.params['w2'])
grads['b2'] = numerical_gradient_onenumber(loss_W, self.params['b2'])
return grads
# 自变量x只能是一个数
def numerical_gradient_onenumber(f, x):
h = 1e-4
# 因为修改了x 也就是params[]所以会计算出f(x+h) 实际上x+h不是作为参数传递到f中的,而是直接改变了f原有参数的值
# 所以真正其作用的是“x = x + h”和“x = temp - h”
temp = x
x = x + h
fxh1 = f(x)
x = temp - h
fxh2 = f(x)
grad = (fxh1+fxh2)/2
x=temp
return grad
# 自变量x只能是一维矩阵
def numerical_gradient_1d(f, x):
h = 1e-4
grad = np.zeros_like(x)
# x是[x1,x2,.....] f是f(x1,x2,.....)
for i in range(x.size):
temp=x[i]
x[i]=x[i]+h
fxh1=f(x) # 计算f(x+h) 因为是多元函数,所以只有xi加上h 其他x不加
x[i]=temp
x[i]=x[i]-h
fxh2=f(x)
grad[i]=(fxh1+fxh2)/2
x[i]=temp
return grad
# 自变量可以是二维矩阵 但是处理办法比较粗暴,就是批次中每一条都进行数值微分
def numerical_gradient_2d(f, x):
if x.ndim == 1:
return numerical_gradient_1d(f, x)
else:
grad = np.zeros_like(x)
for i, x_i in enumerate(x):
grad[i] = numerical_gradient_1d(f, x_i)
return grad
这里需要说明的有:
一,因为偏置b是一个数,而权重w是一个矩阵,所以为它们提供了不同的数值微分方法,但是其本质是一样的。等到后面实现了批处理或者采用误差反向传播求导之后,偏置b和权重w就可以用同一个方法计算梯度啦。
二,lambda表达式,loss_W=lambda w:self.loss(x,t)这一行代码将前面两步封装为一个lambda函数,可以作为参数传递给别的方法使用。
可以看到,这个lambda函数式子中的参数’w’并没有很么作用,根本没有传递到参数里面去。
也就是说“fxh1 = f(x)”这一行代码写成“fxh1 = f(1) fxh1 = f(2)“或者给f的参数传递任何数都是可以的。因为真正起作用的是“x = x + h”和“x = temp - h”它们改变了params里面的值!!,在调用f()之后会执行”y=self.predict(x) return cross_entropy_error(y,t)“这两行代码,而self.predict中用到的params被修改了,因此可以出x+h处的函数值。
下面写一个例子验证一下:
def add(x,y):
return x+y
def use(f,a):
z1=f(a)
print(z1)
afunction = lambda w: add(1, 2)
use(afunction,5)
use(afunction,6)
use(afunction,100)
3.两层神经网络的使用
至此,我们简单的两层神经网络的类就写完了,接下来就是使用了。不过再次强调,这个神经网络设计简单没有实现批处理,没有使用误差反向传播计算梯度,效率非常非常低,这里只是介绍使用流程。也是因为这个原因,在使用这个类的时候不得不做了很多妥协,比如“从60000条训练数据中抽取一部分用来训练”、“迭代次数只有5次”,即使这样也花费了很长时间,所以对于完整的代码(我把它放在了最后)你需要关注的只有以下三点:
一、
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
这里的(x_train, t_train)是训练数据,用于对神经网络的学习,其中的t_train是监督数据,也就是存放手写数字的结果标签。可以参考下图来理解。

(x_test, t_test)是测试数据,用于验证神经网络的学习结果。
二、
network=Myself_Two_Layer_Net(input_size=784, hidden_size=50, output_size=10,weight_init_std=0.01)
因为是训练MNIST手写数字识别,原图像是28像素 × 28像素的形状 为了便于训练,在这里将它扁平化为有784个元素的一维矩阵。所以输入层有784个神经元。因为最终输出的结果是0-9十个数字的分类,所以输出层有10个神经元。
隐藏层的神经元数量是超参数,它的设计属于神经网络的优化内容,这里暂时设为100。
三、
learning_rate = 0.1 # 学习率
# 以及
# 计算梯度
grad = network.gradient_numerical(x_train_one, t_train_one)
# 根据梯度更新参数
for key in ('w1', 'b1', 'w1', 'b2'):
network.params[key] -= learning_rate * grad[key]
学习率也是一个超参数,它表示每次更新参数的幅度。
更新参数的方法也很简单啦,因为沿着梯度方向更新即可。
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
# 这里使用别人写好的数据导入工具
from dataset.mnist import load_mnist
# 导入我们刚刚写好的两层神经网络类
from * * * import Myself_Two_Layer_Net
# 导入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network=Myself_Two_Layer_Net(input_size=784, hidden_size=50, output_size=10,weight_init_std=0.01)
learning_rate = 0.1 # 学习率
iters_num = 5 # 适当设定循环的次数 因为这种实现太慢了所以循环次数设置的少一些
train_size = x_train.shape[0]
test_size = x_test.shape[0]
# train_size是训练数据规模 60000 如果不进行批处理就要循环60000次
# 循环次数太多 太慢 所以从所有的600000条训练数据中随机选取100条
mask1 = np.random.choice(train_size, 100)
x_train_part=x_train[mask1]
t_train_part=t_train[mask1]
for i in range(iters_num):
for j in range(x_train_part.shape[0]):
x_train_one=x_train_part[j]
t_train_one=t_train_part[j]
# 计算梯度
grad = network.gradient_numerical(x_train_one, t_train_one)
# 根据梯度更新参数
for key in ('w1', 'b1', 'w1', 'b2'):
network.params[key] -= learning_rate * grad[key]
print("ok"i,j)
#因为没有实现批处理且采用数值微分,计算准确率会很慢,所以我们只在最后做一次准确率计算 而且只能抽样计算,不然会很慢很慢
# 当前网络对于训练数据的准确率
train_acc=0
for i in range(x_train_part.shape[0]):
train_acc += network.accuracy(x_train_part[i], t_train_part[i])
# 从所有的100000条训练数据中随机选取100条
mask2 = np.random.choice(test_size, 10)
x_test_part=x_test[mask2]
t_test_part=t_test[mask2]
# 当前网络对于测试数据的准确率
test_acc=0
for i in range(x_test_part.shape[0]):
test_acc += network.accuracy(x_test_part[i], t_test_part[i])
print("train acc, test acc | " + str(train_acc/100) + ", " + str(test_acc/100))