论文笔记之超分二：IKC-MetaSR-ODEInspired

2019前超分文章记录 SRCNN-FSRCNN-ESPCN-VDCN-DRCN-RDN-LapSRN-SRDenseNet

2019CVPR超分文章记录系列一：FSTRN-resLR-SRFBN-RBPN

1.Blind Super-Resolution With Iterative Kernel (IKC)

1.1 介绍

当预先定义的模糊核与实际模糊核不同时，基于学习的方法将遭受严重的性能下降。
将未知模糊核的超分问题我们定义为blind SR。这种设置比较符合实际真实情况。**所以这篇文章解决的是超分里面的一个blind super-resolution问题。**这个问题假设下采样的核是未知的。
由核不匹配引起的artifacts是有规则的模式。这种核不匹配影响的不对称性为作者如何纠正不精确的模糊核提供了经验指导。提出了一个Iterative Kernel Correction (IKC) 方法实现predict-and-correct原则，（。作者发现以图像和模糊核的concate作为输入不是最佳选择。采用了空间特征变换（SFT）层，提出一个用于多种模糊核的结构（SFTMD）。通过组合IKC和SFTMD，实现超分目标。

1.2 方法

1.2.1 问题定义

blind SR问题定义如下，HR图像和LR图像之间有一个退化模型
$$I^{LR}=(k\otimes I^{HR}{\downarrow }_s+n$$
$\otimes$代表卷积计算，blur kernel是$k$,降采样操作是${\downarrow }_s$,加上噪声$n$，本文只考虑不带运动模糊的各项异性模糊核（isotropic blur kernel）。文章考虑高斯模糊和双三次下采样的组合，同时加性噪声用高斯扰动模型。

1.2.2 动机

HR图片$I^{HR}$首先由各向异性的高斯核模糊（kernel width ${\sigma }_{LR}$），假设映射$F(I^{LR},k)$是训练良好的SR模型，以核信息为输入，然后输出图像无伪影和正确的核k。blind SR（盲超分）问题就相当于找到核$k$ 帮助SR模型产生视觉效果良好的图像$I^{SR}$。一个直接的方法就是采用一个预测方程$k^{{}^{\prime }}=P(I^{LR})$,从输入的低像素图像直接预测$k$。预测可以通过下面优化
${\theta }_P=argmi{n}_{{\theta }_P}||k-P(I^{LR};{\theta }_P)|{|}_2^2$
通过这种方式建立盲超分模型。
但是准确预测$k$是很困难的，反过来说，对于一个输入可以又多个$k$，错误的$k$会导致明显的伪影，图片处理结果比真是结果增强或者模糊。于是作者提出一个iteratively correct kernel直到获取正确的SR图像。
为了估计$k$，作者建立了一个校正函数$C$用于比较估计的核和真实的核的差别。作者一个核心观点是采用中间的SR结果，矫正方程通过最小化矫正过的核核gt的$l_2$距离得到。
$${\theta }_C=argmi{n}_{{\theta }_C}||k-(C(I^{SR};{\theta }_C)+k^{{}^{\prime }})|{|}_2^2$$
${\theta }_C$是矫正函数$C$的参数，$I^{SR}$是最后的超分结果。
如果只是用一次矫正，结果可能不好，比较好的方法是小步长地矫正。

1.2.3方法

总体结构：包括了超分模型$F$，预测器$P$，矫正器$C$。伪代码如图：

首先假设图片大小为$I^{LR}=C\ast H\ast W$， 假设模糊核大小为$l\ast l$，这是一个$l^2$-维度的线性空间，为了减小运算，先对核做PCA处理降维，投影到$b$-维度线性空间，通过一个$M\in R^{b\ast l^2}$的矩阵。只需要在低维空间做估计。降维后的核我们表示为$h$，$h=Mk$。初始的$h_0$通过预测方程$h_0=P(I^{LR})$得到，然后用来做第一次超分$I_0^{SR}=F(I^{LR},h_0)$。获得初始预测后，进入估计核的校正阶段。在第$i$次迭代，上一次的估计是$h_{i-1}$，上一次更新的结果是$\Delta h_i$，新的预测$h_i$，新的超分图片为
$\Delta h_i=C(I_i^{SR},h_{i-1})$
$h_i=h_{i-1}+\Delta h_i$
$I_i^{SR}=F(I^{LR},h_i)$

1.2.4 SR模型F的网络结构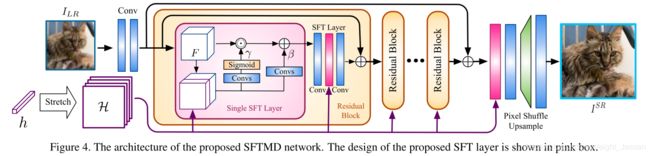

之前一个工作SRMD的做法是先将核$h$扩展成kernal maps，大小为$b\ast H\ast W$，第$i$层所有的元素都等于$h$的第$i$个值。然后将kernal map核图片大小concate起来，大小为$(b+C)\ast H\ast W$。然后是级联的$3\ast 3$卷积核，一个pixel-shuffle上采样层用于超分。但是，为了探索kernel的信息，将图片核转换后concate起来也不是最好的，或者不是唯一的方式。核并没有图片的信息，同时处理核核图片的信息会产生与图像无关的干扰。同时核只是在第一层输入，深度网络很难对第一层的信息做调整。所以作者提出了一个新的SR模型，使用spatial feature transform(SFT)层。
在SFTMD中，核映射通过SFT对每个中间层特征应用仿射。网络设计使用了high-level的SRResNet，扩展成SFT层，通过缩放和移位操作为以核映射H为条件的特征映射F提供仿射变换。通过应用缩放核和平移对特征$F$产生影响
$SFT(F,H)=\gamma \odot F+\beta$
$\odot$表示Hadamard product，假设上一层$F$的输出是$C_f\ast H\ast W$, 那么concate起来的特征是$(b+C_f)\ast H\ast W$。网络根据这些特征，得到$\gamma$和$\beta$。SFT模块用在了residual blocks的卷积层还有global residual connection之后。

1.2.5 Network architecture of predictor $P$ and corrector $C$

对于预测器，用的是四个带有Leaky ReLU的卷积层和一个全局池化层。卷积层给出核h在空间上的估计，并形成估计映射。池化层在空间上取平均值给出全局估计。
对于矫正器，包括了两个输入，通过下面的公式优化：
$${\theta }_C=argmi{n}_{{\theta }_C}||k-(C(I^{SR};{\theta }_C)+k^{{}^{\prime }})|{|}_2^2$$
输入的$I^{SR}$图像通过前面的卷积，可以提取除伪影。然后扩展$f_h$到$F_h$，将$F_{SR}$和$F_h$concate起来，预测$\Delta h$。

1.3 数据预处理

For the isotropic Gaussian blur kernels used for training, the ker- nel width ranges are set to [0.2, 2.0], [0.2, 3.0] and [0.2, 4.0] for SR factors 2, 3 and 4, respectively. The kernel size is fixed to 21×21. When applying on real world images, we use the additive Gaussian noise with covariance σ = 15.
同时提供了test kernel.

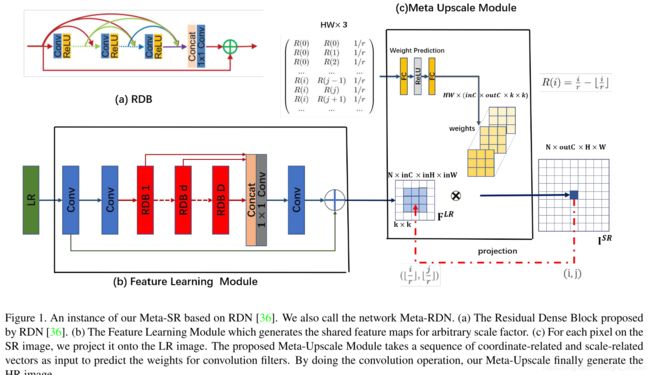
2.Meta-SR: A Magnification-Arbitrary Network for Super-Resolution

本文实现了任意放大比例，可以非整数的。通过一个Feature Learning Module和Meta- Upscale Module实现。

2.1 Method

如图所示，网络分成了两部分，低像素图片的特征提取和元上采样模块。假设高像素图像为$I^{HR}$，采样得到的低像素图像为$I^{LR}$，网络超分得到的图像是$I^{SR}$。对于特征提取网络，采用的是RDN模块。用$F^{[}ba{o}^{\prime }zhe表示提取出来的特征，假设缩放因子是$r$，对于SR图像里的每个像素$(i, j)$,我们认为它是由低像素图像上像素$(i^{’},j{’})$特征和对应滤波器的权重决定。从这个角度看，可以把upsacle模块堪称是一个从$I^{SR}$到$F{SR}$的映射过程。首先上采样模块将$(i,j)$映射到$(i^{’}, j^{{’})$。然后需要一个特定的滤波器让$(i}{’},j^{’})$产生像素$(i,j)$。我们将上采样模块表示为：
$$I^{SR}(i,j)=\Phi (F^{LR}(i^{{}^{\prime }},j^{{}^{\prime }}),W(i,j))$$

那么这里没改像素都要有一个对应的滤波器。对于不同的缩放因子，需要不同的模型，作者提出一个Meta-Upsacle Module实现基于缩放因子和坐标信息动态预测权重$W(i,j)$。

对于Meta-Upscale Module，有三个重要的方程。

• Location Projection 将像素映射都低像素
• Weight Prediction 预测预测sr图像每像素点的权重
• Feature Mapping 将具有预测权重的特征映射回SR图像，计算像素值。

Location Projection

对于每个SR上的每个像素$(i,j)$，location projection就是找到在$(i^{{}^{\prime }},j^{{}^{\prime }})$在LR图像上的位置。作者用了下面的映射操作：
$$(i^{{}^{\prime }},j^{{}^{\prime }})=T(i,j)=(\lfloor \frac{i}{r}\rfloor ,\lfloor \frac{j}{r}\rfloor )$$
位置投影可以看作是一种可变的分数步长的机制，它可以用任意比例因子对特征地图进行升级。
如图所示，如果r是2，那么每个pixel$(i^{{}^{\prime }},j^{{}^{\prime }})$ 就对应两个点。

Weight Prediction

Meta-Upscale Module使用一个网络去预测滤波器的权重
$$W(i,j)=\varphi (v_{ij};\theta )$$
$W(i,j)$是SR图形上像素$(i,j)$上滤波器的权重。$v_{ij}$是一个和$i,j$有关的向量，$\varphi (.)$是预测网络。
对于像素$(i,j)$的$\varphi (.)$输入，使用$(i^{{}^{\prime }},j^{{}^{\prime }})$的相对位移，$v_{ij}$可以表示成：$$v_{ij}=(\frac{i}{r}-\lfloor \frac{i}{r}\rfloor ,\frac{j}{r}-\lfloor \frac{j}{r}\rfloor )$$
为了让网络学到多缩放因子，把缩放因子也加入到向量$v_{ij}$里面，所以把$v_{ij}$记成：
$$v_{ij}=(\frac{i}{r}-\lfloor \frac{i}{r}\rfloor ,\frac{j}{r}-\lfloor \frac{j}{r}\rfloor ,\frac{1}{r})$$

Feature Mapping

从$F^{LR}$上提取到低像素图像上$(i^{{}^{\prime }},j^{{}^{\prime }})$的特征bao，预测滤波器的最终。最后就是将特征映射到SR图像上。使用
$$\Phi (F^{LR}(i^{{}^{\prime }},j^{{}^{\prime }}),W(i,j))=F^{LR}(i^{{}^{\prime }},j^{{}^{\prime }})W(i,j)$$

3 ODE-inspired Network Design for Single Image Super-Resolution

3.1 ODE-inspired network design for SISR

在CNN语义中，时间范围x对应于可自适应选择的层，而最终状态则受标签的限制。关键是设计一个网络实现这个目标。

Mapping numerical ODEs to building blocks In

我们定义可以描述为ODE的动力系统：
$$\frac{dy}{dx}=f(x,y)$$
系统提供了一个映射$\Phi (y_0,x)=y(x;y_0)$
初始 $y_0\in R^d$，假设$p_0$ 是输入特征$y_0$在空间$\Omega$的分布，将CNN-base超分看成一个动态系统，假设$$L={\int }_{\Omega }||\Phi (y_0,x)-y||dp(y_0)$$
其中$\Phi$是要学习的映射,和第一个方程的解有联系。
前向欧拉法里面：$y_{n+1}=y_n+hf(x_n,y_n)$，在微积分里面$y_{n+1}-y_n\approx h{y}^{{}^{\prime }}$。Residual blaock的形式是$y_{n+1}=y_n+G(y_n)$。所以我们可以得到$$G(y_n)=hf(x_n,y_n)$$

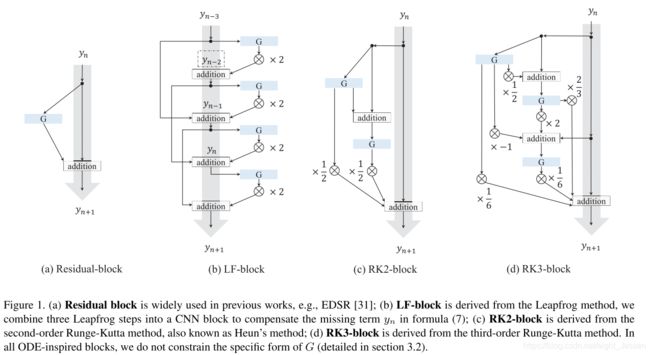
3.1.1 LF-Block

可以有$y^{{}^{\prime }}\approx (y_{n+1}-y_{n-1})/2h$，即可以得到下面的方程
$$y_{n+1}=y_{n-1}+2hf(x_n,y_n)$$
同理有$y_n,y_{n-1}$，对应于Fig b。这里没有限制G是一个固定的模块。

3.1.2 RK2-Block

梯形公式
$y_{n+1}=y_n+\frac{h}{2}(f(x_n,y_n)+f(x_{n+1},{\hat{y}}_{n+1}))$
将${\hat{y}}_{n+1}$换成$y_{n+1}=y_n+hf(x_n,y_n)$，有
$y_{n+1}=y_n+\frac{1}{2}(G_1+G_2)$
$G_1=hf(x_n,y_n)$
$G_2=hf(x_n+h,y{n}_n+G_1)$
网络结构如图1 c

3.1.3 RK3-Block

Runge-Kutta方法可以写成任意$n$阶通过
$y_{n+1}=y_n+{\sum }_{i=1}^n{\gamma }_i{G}_i$
$G_1=hf(x_n,y_n)$
$G_i=hf(x_n+{\alpha }_{i}h,y_n+{\sum }_1^{i-1}{\beta }_{ij}{k}_j)$
比如对于3阶Lunge-Kutta
$y_{n+1}=y_n+\frac{1}{6}(G_1+4G_2+G_3)$
$G_1=hf(x_n,y_n)$
$G_2=hf(x_n+\frac{h}{2},y_n+\frac{1}{2}{G}_1)$
$G_3=hf(x_n+h,y_n-G_1+2G_2)$

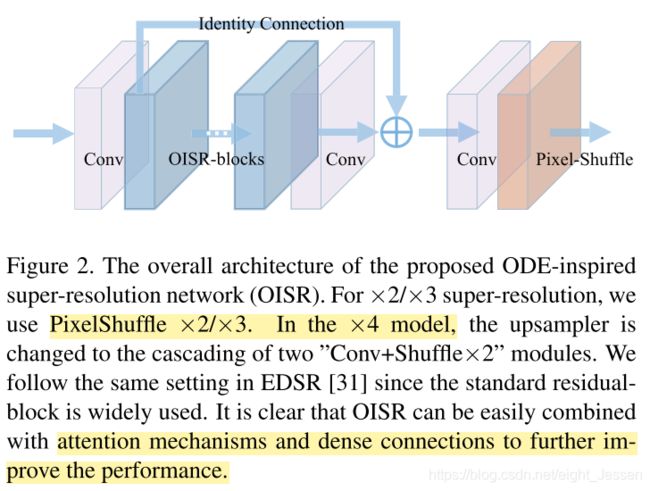
3.2 OISR总体结构

总体结构是一个Convolution-PixelShuffl框架。如果不限制在有限步，最终$h_n$可以趋于0
最终实验设计比较了不同方式下，不同模块$G$的结果
还有和以往不同网络的结果比较

G的不同形式，每种形式至少保留一个激活方程和一个卷积，保证非线性，实际上不同的数值方法对应不同的策略。无论是高阶方法还是改进的G都有助于提高性能：