逻辑回归实战--信用卡欺诈检测(一)

首先导入所需要的工具包。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

接下来导入数据

点击下方链接获取数据：
https://download.csdn.net/download/weixin_42410915/12822262

data = pd.read_csv('c:/users/lenovo/Desktop/card.csv')
data.head() #默认展示数据的前5行记录

原始数据为个人交易记录，该数据总共31列，其中数据特征有30列，Time列暂时不考虑，Amount列表示贷款的金额，Class列表示分类结果，0为交易记录正常，若Class为1代表交易异常。

实际生活中，正常交易占绝大多数，异常交易仅占一小部分。由于数据太多，查看异常交易的情况有些麻烦，value_counts()函数可以算出数据中有哪些不同值，并计算每个值有多少个重复值。由此可以得到异常交易的数量。

count_classes = data['Class'].value_counts()
count_classes

结果如下：

但是绘制一张图表是不是更能清晰地表达交易状况呢？

此时需要将pandas和matplotlib库结合一下。

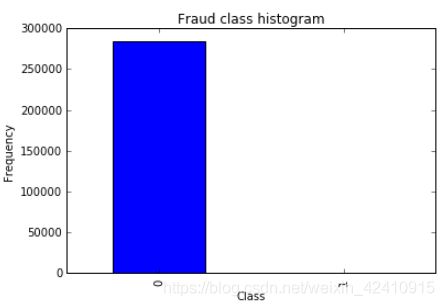
count_classes.plot(kind='bar')
plt.title('Fraud class histogram')
plt.xlabel('Class')
plt.ylabel('Frequency')

结果如下:

不管从数据还是从图表中都可知异常数据非常少，而我们的目标就是找到异常数据，如果搭建的模型不重视极少数数据，结果就没有意义了，所以，要改进数据的不平衡性。 解决数据不平衡问题，让两者的数据相差不大即可。通常采用下采样、过采样这两种方法。

下采样：若一组的数据非常少，让另一组数据变少，使两者比例均衡。即从正常数据中随机抽取大约500条数据即可。看似方法挺简单，但只利用了上万条数据中的一小部分，会不会对结果产生影响呢?

过采样：不放弃任何一条数据，通过制造出一些异常数据，让两组数据一样多。数据生成也是现阶段常见的一种方法。但是假设得到的数据是否符合真实情况，对结果造成影响呢？

前辈说：数据特征决定结果的上限，模型的调优只决定如何接近这个上限。 机器学习的核心其实都在数据处理中，数学建模只是其中一部分。

from sklearn.preprocessing import StandardScaler

#将Amount标准化，并赋给新的列NormAmount
data['NormAmount'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1,1))
data = data.drop(['Time','Amount'],axis=1) #删除Time和Amount两列数据
data.head()

下面进行下采样操作

'''
下采样
'''

#取出包含Class这一列的数据
X = data.ix[:, data.columns != 'Class']

#标签，取出Class这一列数据，并计算有几个异常
y = data.ix[:, data.columns == 'Class']
number_records_fraud = len(data[data.Class==1])

#取出异常样本的行索引
fraud_indices = np.array(data[data.Class==1].index)
#取出正常样本的行索引
normal_indices = np.array(data[data.Class==0].index)

#随机选取一些正常样本，数量和异常样本数量一致
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace=False)
#将上述数据转换为numpy形式
#random_normal_indices1 = np.array(random_normal_indices)

#将正常和异常索引合并
under_sample_indices = np.concatenate((fraud_indices,random_normal_indices), axis=0)
#得到下采样数据集
under_sample_data = data.loc[under_sample_indices,:]
#下采样数据集的数据
X_undersample = under_sample_data.ix[:, under_sample_data.columns != 'Class']
#下采样数据集的标签
y_undersample = under_sample_data.ix[:, under_sample_data.columns == 'Class']

#计算下采样后正负样本比例
print('下采样后异常样本比例:', (y_undersample==1).sum()/len(under_sample_indices))
print('下采样后正常样本比例:', (y_undersample==0).sum()/len(under_sample_indices))
print('下采样后总样本数量：', len(under_sample_indices))

 结果如下：

在这里介绍一下np.random.choice()函数。 data = np.random.choice(a,n,replace=False,p=None) 上述代码意思是从a中随机选取n个数据，p没有指定的时候相当于数据a分布一致；

data = np.random.choice(a,n,relace=Flase,p=[0.2,0.1,0.4,0.3]) 当p指定时，即数据a分布不一致，按照给定的比例从a中抽取n个数据。

replace指是否是重复抽样，即抽取后的数据是否还放回原数据集中再次参与抽取。若为True，可能会出现重复的数据，这样会减少样本的多样性。

上述输出结果表明，经下采样后，共有984条数据，正常/异常样本均占一半，此时数据满足平衡标准

下面来划分数据集。在机器学习中，当训练集进行建模时，会涉及一些参数调整，此时需要一些验证集，帮助模型进行参数的调整和选择。当训练集完成建模后，还需要知道这个模型的好坏，也就是需要一个测试集。

需要注意，测试集和训练集的数据不能有重叠部分，否则就相当于提前告诉考生答案，最终评估结果不准确。训练集和测试集的比例可自行设定。

在训练集建立模型时，由于需要同步验证，所以可将训练集分成多份，这里假设10份。在验证时，第一步用前9份作训练集，最后一份作验证集，得到一个结果。以此类推，第十个结果就是由后9份作训练集，第一份作验证集得到的。这10个结果分别对应其中每一小份，组合起来恰好包含整个训练集中所有数据，再对这10个结果取平均值，就得到最终验证结果。这个过程叫做交叉验证。

将下采样后的数据进行划分

from sklearn.cross_validation import train_test_split

#X是特征数据，y是标签，test_size是测试集比例，random_state是随机种子，令每次随机得到的结果一样
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
print('原始训练集的样本数量:', len(X_train))
print('原始测试集的样本数量:', len(X_test))
print('原始样本总数量:', len(X_train)+len(X_test))

#对下采样数据集进行划分
X_train_undersample,X_test_undersample,y_train_undersample,y_test_undersample = train_test_split(X_undersample,
                                                                                                y_undersample,
                                                                                                 test_size=0.3,
                                                                                                random_state=0)
print('下采样训练集的样本数量:', len(X_train_undersample))
print('下采样测试集的样本数量:', len(X_test_undersample))
print('下采样样本总数量:', len(X_train_undersample)+len(X_test_undersample))

 结果如下：

设定不同的阈值0.01，0.1，1，10，100，进行逻辑回归，计算出没一个阈值对应的平均召回率，并得到模型效果最好时的阈值

from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import KFold,cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report

def printing_Kfold_scores(x_train_data, y_train_data):
    
    #第一个参数：训练集的长度；第二个参数：输入的几折交叉验证
    fold = KFold(len(y_train_data), 5, shuffle=False)
    #定义不同的正则化惩罚力度
    c_param_range = [0.01,0.1,1,10,100]
    #将结果用表格形式表示
    results_table = pd.DataFrame(index = range(len(c_param_range),2),
                                columns=['C_parameter','Mean recall score'])
    results_table['C_parameter'] = c_param_range
    
    #k-fold表示K折的交叉验证，在此设定了两个索引集合：训练集=indices[0],验证集=indices[1]
    j = 0
    
    #循环遍历不同的参数
    for c_param in c_param_range:
        print('------------------------------------')
        print('正则化惩罚力度:', c_param)
        print('------------------------------------')
        recall_accs = []
        
        #一步步分解执行交叉验证
        for iteration,indices in enumerate(fold,start=1):
            #制定算法模型，设定参数
            lr = LogisticRegression(C=c_param,penalty='l1')
            #用训练集建立模型，因用的都是训练集，故索引均为0
            lr.fit(x_train_data.iloc[indices[0],:],
                   y_train_data.iloc[indices[0],:].values.ravel())
            #建立好模型后，用验证集验证模型，索引为1
            y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
            #预测结果明确后，进行模型评估。recall_score传入预测值和真实值
            recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,
                                      y_pred_undersample)
            #后续需要平均值，故将每一步的结果进行保存
            recall_accs.append(recall_acc)
            print('Iteration',iteration, '召回率:',recall_acc)
        
        #执行完所有的交叉验证后，计算平均值
        results_table.loc[j, 'Mean recall score'] = np.mean(recall_accs)
        j = j+1
        print('')
        print('平均召回率:', np.mean(recall_accs))
        print('')
        
    #因为召回率越高越好，所以查找Recall值最高的参数
    best_c = results_table.loc[results_table['Mean recall score'].astype('float32').idxmax()]['C_parameter']
    
    #输出最好的结果
    print('********************************************')
    print('效果最好的模型所选参数=', best_c)
    print('********************************************')
    return best_c

best_c = printing_Kfold_scores(X_train_undersample, y_train_undersample)

 结果如下：

------------------------------------
正则化惩罚力度: 0.01
------------------------------------
Iteration 1 召回率: 0.931506849315
Iteration 2 召回率: 0.917808219178
Iteration 3 召回率: 0.983050847458
Iteration 4 召回率: 0.959459459459
Iteration 5 召回率: 0.954545454545

平均召回率: 0.949274165991

------------------------------------
正则化惩罚力度: 0.1
------------------------------------
Iteration 1 召回率: 0.849315068493
Iteration 2 召回率: 0.86301369863
Iteration 3 召回率: 0.949152542373
Iteration 4 召回率: 0.945945945946
Iteration 5 召回率: 0.909090909091

平均召回率: 0.903303632907

------------------------------------
正则化惩罚力度: 1
------------------------------------
Iteration 1 召回率: 0.849315068493
Iteration 2 召回率: 0.890410958904
Iteration 3 召回率: 0.983050847458
Iteration 4 召回率: 0.945945945946
Iteration 5 召回率: 0.924242424242

平均召回率: 0.918593049009

------------------------------------
正则化惩罚力度: 10
------------------------------------
Iteration 1 召回率: 0.876712328767
Iteration 2 召回率: 0.890410958904
Iteration 3 召回率: 0.983050847458
Iteration 4 召回率: 0.945945945946
Iteration 5 召回率: 0.939393939394

平均召回率: 0.927102804094

------------------------------------
正则化惩罚力度: 100
------------------------------------
Iteration 1 召回率: 0.890410958904
Iteration 2 召回率: 0.890410958904
Iteration 3 召回率: 0.983050847458
Iteration 4 召回率: 0.945945945946
Iteration 5 召回率: 0.939393939394

平均召回率: 0.929842530121

********************************************
效果最好的模型所选参数= 0.01
********************************************

在sklearn工具包中，C参数的含义正好是相反的。当C=0.01时，表示正则化力度较大；而C=100时，表示正则化力度较小。

到此已经完成建模的基本调参任务，最好的结果在95%左右，感觉好不错。若还想要模型具体表现，需要再更进一步分析。。。