LeNet、AlexNet、VGG卷积神经网络
对卷积和池化过程有了基本认识之后,这篇文章梳理LeNet、AlexNet以及VGG这三个经典的卷积神经网络,并通过代码实现其网络结构来加深理解。
LeNet
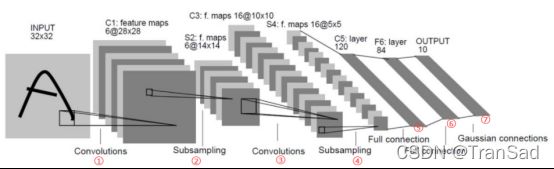
LeNet是最早发布的卷积神经网络之一了,LeNet是最早用来处理手写字体识别任务的网络,是非常简单而又经典。一般来说手写字体识别传入的图像是28*28的,但这里一开始先进行了padding=2的填充再卷积,所以下面图中input是32*32,这一点不同理解即可。对于每一步卷积以及池化(图中Subsampling降采样)我都做了标记,其具体操作解释对应着第二张图。
可以看到LeNet-5一共有5层:包括2个卷积层以及3个全连接层。就是这样通过几次卷积+池化的再送入最终的全连接层,我们就得到了十维的输出用于做分类结果。
LeNet参考代码:
LeNet = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))原模型最后一层是高斯连接(好像用的不太多),代码里就是普通的全连接层。其他部分就是正常的LeNet-5网络。
AlexNet
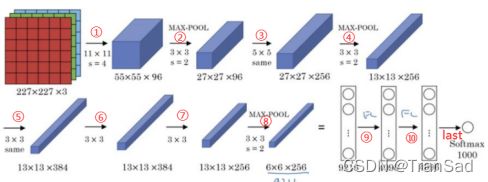
AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的。其网络结构如图所示(在上篇讲卷积尺寸变化时就用了这幅图):
从图中可以看到AlexNet总共有有8层——包括5层的卷积(①③⑤⑥⑦)以及3层的全连接(⑨⑩和last)。
我在图中每一个箭头都做了标记,其对应的操作如下:(CONV是卷积,MAX POOL是池化,FC(full-connect)是全连接)
此外,AlexNet也使用了dropout、relu激活函数等在当时来说较新的技术点,在图中并没有出现,在下面的代码实现中会体现。
AlexNet参考代码:
import torch
from torch import nn
AlexNet = nn.Sequential(
nn.Conv2d(3, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 使用三个连续的卷积层和较小的卷积窗口
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),#打平操作,开始进行全连接层
# 使用dropout层来减轻过拟合
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 1000))VGG
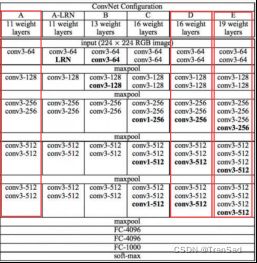
VGG网络有很多种,有VGG11,VGG16以及VGG19等。它们的不同之处在于卷积层的个数不同(VGG11有8层卷积、VGG16有13层卷积、VGG19有16层卷积),全连接层都是3层。
(这张表中每一列代表不同层数的VGG网络(框起来的三个分别就是VGG11,VGG16以及VGG19的卷积层部分,它们最后都带着三个同样的全连接层)。而其中的内容比如conv3-256表示此时使用256个3*3的卷积核进行卷积,下一步将得到256个特征图)
不同于AlexNet使用11*11、5*5的卷积核,VGG网络的一大特点就是它的卷积全部是用3*3的卷积核来做。这是因为在实验中发现使用多个3*3的卷积核就可以达到与5*5或11*11这样的大卷积核一样的感受野;此外还顺便增加了网络的深度,增加了使用非线性层来提取特征的次数(卷积的过程越多,特征提取越细致),提高了模型的学习能力;最重要的是,这样做参数还会更少。
举个例子来说明一下使用3*3卷积核对参数量的影响。
对于一个5*5的输入,第一次3*3卷积之后,维度变为3*3,再经过一次3*3卷积,维度变为1*1了;而如果直接用5*5的卷积,维度也可以直接变成1*1。因此我们有非常简单的共识:2次3*3的卷积在尺寸变化(感受野)上等价于一次5*5的卷积;3次3*3的卷积则等价于一次7*7的卷积(道理类似)。
那么为什么使用2次3*3而不是一次5*5呢?假设卷积核通道数为1,且只需要得到一个特征图(卷积核个数也为1),那么前者参数量为2*3*3=18,少于后者参数量5*5=25;使用3次3*3卷积的参数量3*3*3=27更少于使用一次7*7卷积的参数量7*7=49。如果再考虑(乘以)卷积核通道数以及卷积核个数,这个差距会更大。因此VGG通过使用多次小卷积的方式,减少了参数量。
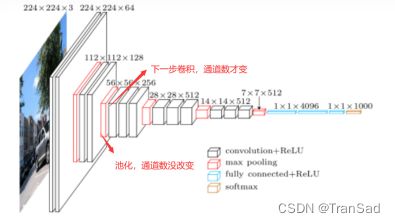
VGG还有一个重要的操作,就是池化之后,为了弥补信息的损失,会通过下一次卷积来使通道数翻倍。注意,这里并不是说池化层使通道数翻倍(池化无法改变通道数),而是池化后的下一次卷积,我们使用翻倍通道数的卷积核来实现通道数翻倍。比如某一次池化之后我们得到了128个特征图,下一步我们直接使用256个卷积核进行卷积。
通过上图我标记的地方可以发现,池化后通道数(深度)并没有改变,等下一次卷积之后,其深度才有了明显的二倍的变化。
做个小结,通过这三个经典的卷积神经网络,可以进一步理解了常见卷积池化过程。这些网络中仍然蕴含着一些其他经典而具有启发性的操作方式,值得进一步学习和探索。