线性模型多分类学习(主要为ECOC技术理论理解)
多分类学习的主要解决思路是把多分类问题拆解成若干个二分类任务求解。首先先对问题拆分,然后根据每个分类任务去设计并训练一个分类器,最后进行测试,在测试时对若干个分类器的预测结果进行集成最后获得多分类结果。
拆分的方法最主要有三种 “一对一(OvO)” “一对余(OvR)” “多对多(MvM)” 。假设数据集D有n个特征分别为C1、C2、C3......Cn。
OvO是将这n个特征进行两两配对,一共会有N(N-1)/2个分类器。假设我们把C1当作我们需要获取的特征C2当作我们需要舍弃的特征,我们就可以把C1当作正例C2当作反例,当我们把数据输送给分类器时,分类器就会进行标记,最后我们把多个分类器进行组合时就可以通过标记的数量(投票)进行取舍。把最多的类别作为最终分类的结果。
OvR是将一个特征作为正例其他作为反例来进行设计分类器,这样就会有N个分类器,每一个分类器代表一个特征。当多个分类器组合时,只包含我们需求的分类器进行输出为正例,那么将输出结果作为最终分类结果。如果有多个分类器预测为正例,则考虑各分类器的置信度(置信度就是用一种方法构造一百个区间如果有95个区间包含总体真值,就说置信度为95%。注意:不是100个值中包含95个真值,是100次测试中有95次测试包含真值),选择置信度最大的类别作为分类结果。
OvR只需要训练n个分类器,而OvO则需要训练N(N-1)/2个分类器,客观来看OvO在储存和测试时间方面要比OvR更长。但是在训练时OvR的每一个分类器都使用全部训练集,而OvO的分类器仅用到了包含两个特征的训练集,因此在很多时候OvO的训练时间要比OvR要短。在测试性能方面则要看具体的数据分布(NFL定理),在大多数情况下两者差距不大。这两种方法由于特征空间中会存在一些无法确定的区域因此不能很好的表示每个特征类别。
MvM是每次将多个特征作为正例多个特征作为反例,显然OvR和OvO是MvM的特例。MvM的正反类(特征描述)必须有特殊的设计,不能随便选取。再此我们使用“ (纠错输出码)ECOC”
ECOC技术是将编码思想引入类别拆分并尽可能在解码过程中具有容错性(原理:当编码足够多时单一编码错误对全局的影响比较小)
编码:对类别做划分,每次划分将一部分类别划为正类,一部分划为反类,从而形成一个二分类训练集;这样一共产生M个训练集,可训练出M个分类器
解码:M个分类器分别对测试样本进行预测,这些预测标记组成一个编码.将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果
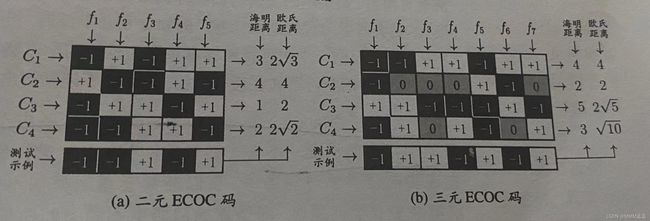
类别划分通过“编码矩阵”指定.编码矩阵有多种形式常见的主要有二元码和三元码前者将每个类别分别指定为正类和反类,后者在正、反类之外,还可指定“停用类”。如图f1把C2当作正例,C134当作反例,f3把c12当作反例把c34当作正例,通过训练各分类器获得一定的识别能力,当测试数据输入时分类器给出判断,在解码阶段各分类器的结果联合起来形成测试示例编码,改编码和图中C1 C2 C2......等这类编码进行欧式距离计算并进行比较,结果最小(代表两个编码最相似)的就所属于的类别。图中预测结果为C3.
一般来说,对同一个学习任务,ECOC编码越长,纠错能力越强.然而编码越长,意味着所需训练的分类器越多,计算、存储开销都会增大;另一方面,对有限类别数,可能的组合数目是有限的,码长超过一定范围后就失去了意义.对同等长度的编码,理论上来说,任意两个类别之间的编码距离越远,则纠错能力越强.因此,在码长较小时可根据这个原则计算出理论最优编码.然而码长稍大一些就难以有效地确定最优编码,事实上这是NP难问题.不过,通常我们并不需获得理论最优编码,因为非最优编码在实践中往往已能产生足够好的分类器.另一方面,并不是编码的理论性质越好,分类性能就越好,因为机器学习问题涉及很多因素,例如将多个类拆解为两个“类别子集”,不同拆解方式所形成的两个类别子集的区分难度往往不同,即其导致的二分类问题的难度不同;于是,一个理论纠错性质很好、但导致的二分类问题较难的编码,与另一个理论纠错性质差一些、但导致的二分类问题较简单的编码,最终产生的模型性能孰强孰弱很难说。
欧式距离(最小二乘法如下图):m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
海明距离:在信息编码中,两个合法代码对应位上编码不同的位数称为码距,又称海明距离。举例如下:10101和00110从第一位开始依次有第一位、第四、第五位不同,则海明距离为3。
bz:本文章源于个人对西瓜书部分内容理解仅用于交流。