误差反向传播的python实现（简单高效计算梯度值）

NN的学习中需要计算权重和偏置参数的梯度，对于梯度的计算，很容易想到数值导数，即前向差分
$$dx=\frac{f(x+h)-f(x)}{h}$$

或者改进一点，用中心差分(更接近准确的导数值)
$$dx=\frac{f(x+h)-f(x-h)}{2h}$$
h取一个接近0的数值，如0.0001

但这样计算是比较慢的，尤其是大型网络，参数众多的情况，所以我们用一种更快的方法计算参数的梯度值——反向传播。

反向传播的精髓，本质，核心是链式法则chain rule

正是链式法则的应用简化了梯度计算，而且链式法则和反向传播都特别简单，非常好理解。

由于太简单，本文跳过原理叙述直接写代码，如果想仔细学习BP可以看斋藤康毅的《Deep Learning from Scratch》（很火的红色封面，有一条灰色的鱼，CSDN下载链接，我下载看过，非常清晰）中第五章关于反向传播的讲解，极为透彻！！！用计算图作为示例，一点一点，推导加法器，乘法器，RELU，sigmoid,softmax，除法器，exp运算，log运算等，总之所有的NN中用到的运算模块的反向导数，还推导了softmax-with-cross_entropy_error层的反向导数求解，得到了极为漂亮的结果，也正是这个结果使得梯度的计算如此简单。

NN的每一层都实现为一个类，包括Affine层，Sigmoid层，Relu层，Softmax-with-Loss层（loss用cross-entropy-error），类中定义前向传播和反向传播的计算方法。

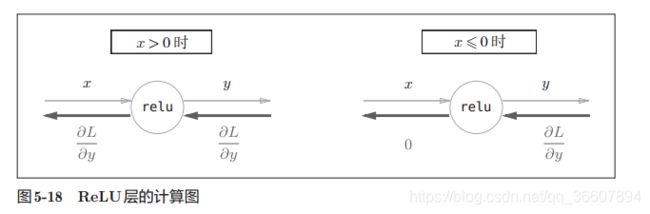
1. Relu层

$$y=\{\begin{array}{r}x,x>0\\ 0,x\le 0\end{array}$$

导数自然就是：
$$\frac{\partial y}{\partial x}=\{\begin{array}{r}1,x>0\\ 0,x\le 0\end{array}$$

代码：

# relu层的类
class Relu:
    def __init__(self):
        self.mask = None

    # 前向传播的计算
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()  # out就等于x
        out[self.mask] = 0

        return out

    # 反向传播的计算
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx

这个比喻可以说是很入骨了···

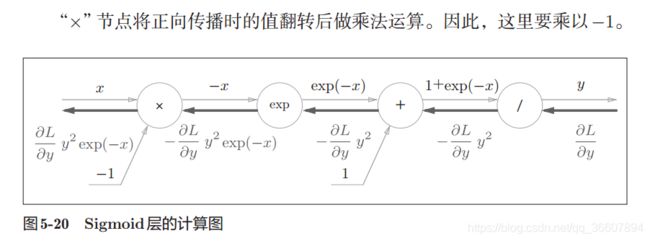
2. Sigmoid层

$$y=\frac{1}{1+exp(-x)}$$

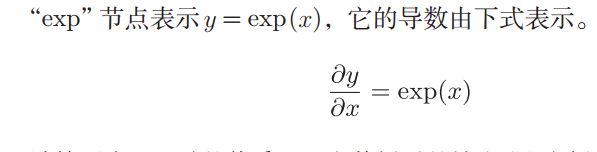
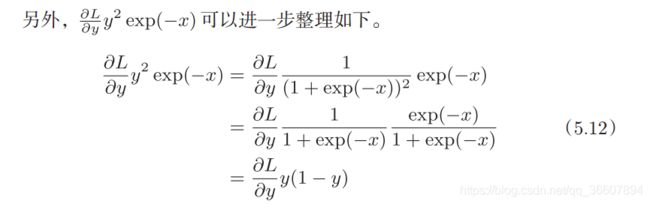
代码：

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / 1 + np.exp(-x)
        self.out = out

        return out

    def backward(self, dout):
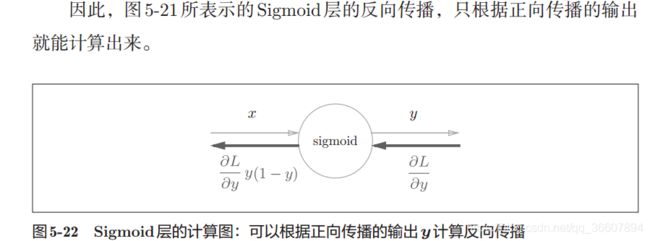
        dx = dout * self.out * (1 - self.out)

        return dx

3. Affine层

NN中前向传播需要用矩阵乘法，在每个学习层都会遇到这样的计算：
$$Y=X.W+B$$
运算里有缩放和平移，在几何学上称为仿射变换（affine），所以我们把这个计算专门定义为一层，叫做affine层，这样每一个学习层都可以重复调用这个类。

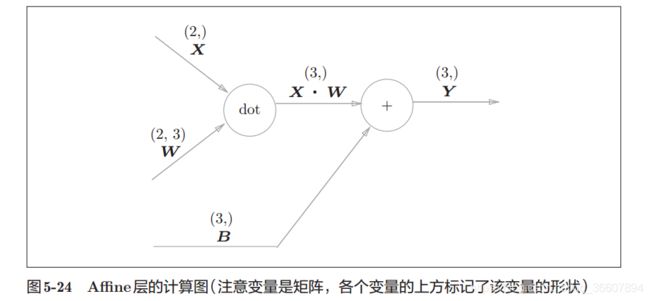
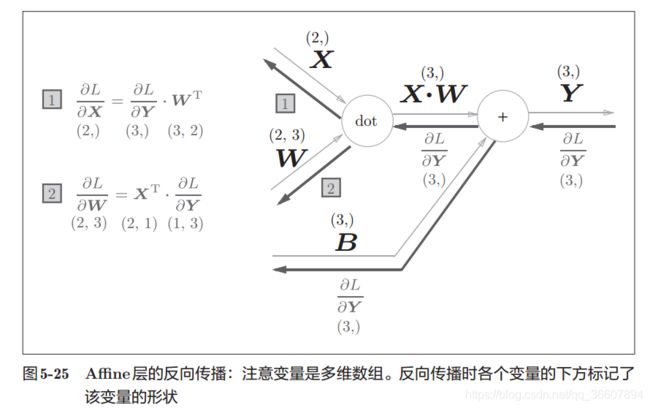
上2图对于理解代码的backward()方法非常重要！！！

5-25是单个输入经过affine层的正向和反向计算，但5-27展示的批版本的才是实用价值更大的，加快计算速度，而且不难，只要理解矩阵乘法就行。

黑色反向粗箭头下面写的是导数值，一点一点，依据链式法则从输出传到输入，L是假设的整个NN的最终输出的损失函数，由于affine层只是NN的一个part，所以反向传播由$\frac{\partial L}{\partial Y}$开始：

• 经加法节点导数不变，只是对偏置求导时，由于示例中偏置是1行3列的，而$X.W$是N行3列的，实际上N行都加了一样的偏置，所以对偏置矩阵B（1行3列）的导数是$\frac{\partial L}{\partial Y}$列方向的和；(第0轴是列方向，第1轴是行方向，第2轴是Z方向)
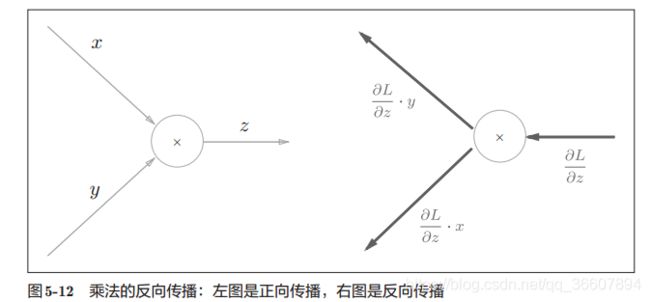
• 经过乘法节点，翻转相乘，得到对X和W的导数，具体为啥左乘右乘还转置从矩阵乘法的合法性上(维度是否可乘)很好理解。

经过乘法节点，翻转相乘的解释：
$$z=xy$$
$$\frac{\partial z}{\partial x}=y$$
$$\frac{\partial z}{\partial y}=x$$

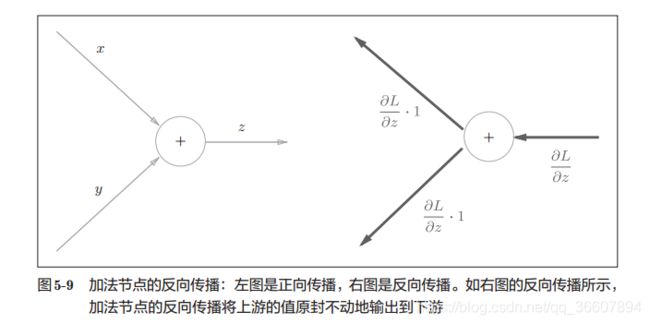
经过加法节点，导数不变的解释：
$$z=x+y$$
$$\frac{\partial z}{\partial x}=1$$
$$\frac{\partial z}{\partial y}=1$$

代码：

class Affine:
    def __init__(self, w, b):
        self.w = w
        self.b = b
        self.x = None
        self.dw = None
        self.db = None
        
        
    def forward(self,x):
        self.x = x
        out = np.dot(x, self.w) + self.b
        
        return out
    
    
    def backward(self,dout):
        dx = np.dot(dout, self.w.T) 
        # 权重经过的是乘法器单元，对数据x求导则让输出dout乘以权重
        # 对权重求导则让dout乘以数据x
        # 偏置经过加法器单元，对b求导就等于对dout求导
        self.dw = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        return dx 

4. Softmax-with-Loss层

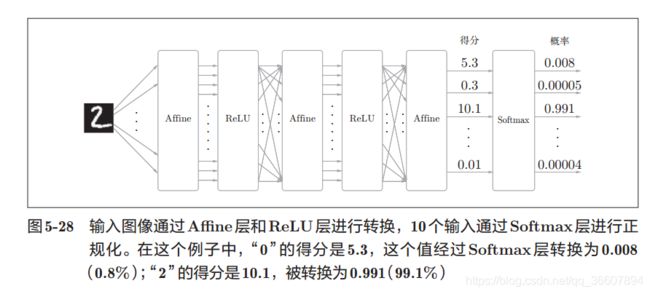
如图，这是一个3层NN（2个隐层）
affine层用于完成每层的加权和偏置计算
隐层用relu激活函数
输出层用softmax激活函数（因为这是分类任务，回归任务用恒等函数作为激活函数）对结果进行正规化（输出的和调整为1），正规化之前的NN输出通常被称为“得分”

注意：NN中有两个阶段，学习和推理。
softmax层只对NN的学习有用，学完之后投入推理阶段后，这一层是可有可无的，毕竟直接选择得分最大的输出作为分类结果也是可以的，所以推理阶段通常不用softmax层。

分类任务中，通常隐层会使用relu居多（比sigmoid的使用更多），而输出层affine完了后是一定会使用softmax激活函数的，并且一定要搭配交叉熵误差损失函数cross-entropy-error，因为这样搭配起来会使得Softmax-with-Loss层得到最简单漂亮的反向导数：

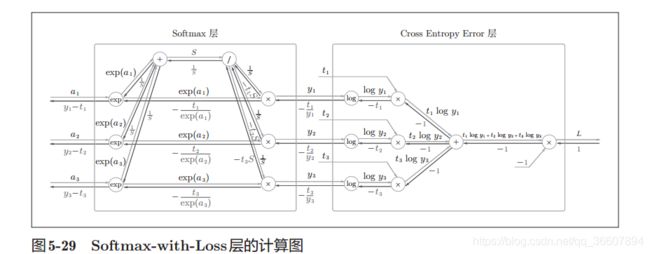
这个图看似很复杂，实际并不难，示例的Softmax-with-Loss层（输出层）有3个输出unit, 即这是个三元分类任务，正向的传播很简单，略过。
反向导数计算：
很显然，L是交叉熵损失，最开始的导数是$\frac{\partial L}{\partial L}=1$

• 经过乘法节点，翻转乘,得-1
• 经过加法节点，导数不变
• 经过log节点，导数除以对应的y值
  
• 后面以此类推，最终得到反向导数就是$y_n-t_n$的简单结果，非常有利于我们高速计算梯度！而不是像文首那样用数值法逼近，计算量更大。

代码：

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a-c) # 防溢出
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size


class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None
        self.t = None  # one-hot vector


    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)

        return self.loss


    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dy = (self.y - self.t) / batch_size
        # 注意反向传播时，将要传播的值除以批的大小（batch_size）后，
        # 传递给前面的层的是单个数据的误差。

        return dy