强化学习RL学习笔记4-马尔可夫决策过程（MDP）(1)

强化学习笔记专栏传送

上一篇：强化学习RL学习笔记3-gym了解与coding实践
下一篇：强化学习RL学习笔记5-马尔可夫决策过程（MDP）(2)

前言

强化学习（Reinforcement Learning, RL），又称再励学习、评价学习或增强学习，是机器学习的范式和方法论之一，用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题 。

本文是笔者对强化学习的一点学习记录，成文于笔者刚开始接触强化学习期间，主要内容参考LeeDeepRL-Notes，学习期间很多概念和理论框架还很不成熟，若文中存在错误欢迎批评指正，也欢迎广大学习者沟通交流、共同进步。

---

Markov Process(MP)（马尔可夫过程）

1.Markov Property（马尔可夫性质）

我们设状态的历史为 $h_t=\left\{s_1,s_2,s_3,\dots ,s_t\right\}$（$h_t$包含了之前的所有状态），如果一个状态转移是符合马尔可夫的，也就是满足如下两个条件：

• $p\left(s_{t+1}\mid s_t\right)=p\left(s_{t+1}\mid h_t\right)$
• $p\left(s_{t+1}\mid s_t,a_t\right)=p\left(s_{t+1}\mid h_t,a_t\right)$

即从当前 $s_t$ 转移到 $s_{t+1}$这个状态，直接等于这之前所有的状态转移到 $s_{t+1}$。如果某一个过程满足马尔可夫性质(Markov Property)，就是说未来的转移跟过去是独立的，它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。

2.Markov Process（马尔可夫过程）

如上图所示，是一个 马尔科夫链(Markov Chain) 的例子。这个图里面有四个状态，这四个状态从 $s_1$,$s_2$,$s_3$,$s_4$之间互相转移。比如说从$s_1$开始：

• $s_1$有0.1的概率继续存活在$s_1$状态。
• 有0.2的概率转移到$s_2$。
• 有0.7的概率转移到$s_4$。

如果$s_4$是当前状态：

• 它有0.3的概率转移到$s_2$。
• 有0.2的概率转移到$s_3$。
• 有0.5的概率留在这里。

我们可以用如上图所示的 状态转移矩阵(State Transition Matrix) 来描述这样的状态转移。状态转移矩阵类似于一个 conditional probability，当我们知道当前我们在 $s_t$ 这个状态过后，到达下面所有状态的一个概念。所以它每一行其实描述了是从一个节点到达所有其它节点的概率。

3.Example of MP

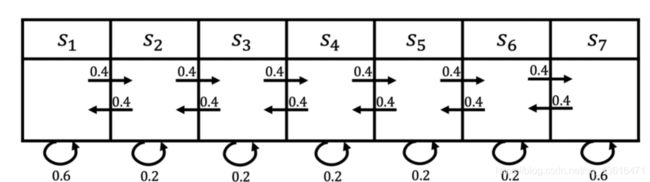
上图是一个马尔可夫链的例子，我们这里有七个状态。比如说从 $s_1$ 开始有 0.4 的概率到 $s_{2}s$，有 0.6 的概率继续存活在它当前的状态 $s_1$ 。 $s_2$ 有 0.4 的概率到 $s_1$ ，有 0.4 的概率到 $s_3$ ，另外有 0.2 的概率存活在 $s_2$ ，所以给定了这个状态转移的马尔可夫链后，我们可以对这个链进行采样，这样就会得到一串的轨迹。

---

Markov Reward Process(MRP)（马尔科夫奖励过程）

马尔可夫奖励过程(Markov Reward Process, MRP) 是马尔可夫链加上一个奖励函数。在 MRP 中，转移矩阵跟状态都是跟马尔可夫链一样的，多了一个奖励函数(reward function)。奖励函数是一个期望，即到达某一个状态的时候，可以获得多大的奖励，然后这里另外定义了一个 discount factor γ 。

1.Example of MRP

上图还是前文解释的马尔可夫链，如果把奖励也放上去的话，就是说到达每一个状态，我们都会获得一个奖励。这里我们可以设置对应的奖励，比如说到达 $s_1$ 状态的时候，可以获得 5 的奖励，到达 $s_7$ 的时候，有 10 的奖励，其它状态没有任何奖励。因为这里状态是有限的，所以我们可以用一个向量来表示这个奖励函数，这个向量表示了每个点的奖励的大小。

2.Return and Value function

这里进一步定义一些概念：

• Horizon 是指一个 episode 的长度（每个 episode 最大的时间步数），它是由有限个步数决定的。
• Return(回报) 说的是把奖励进行折扣后所获得的收益。Return 可以定义为奖励的逐步叠加，如下式所示：$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+...+{\gamma }^{T-t-1}{R}_T$$

上式有一个叠加系数γ，越往后得到的奖励，折扣得越多。这说明我们其实更希望得到现有的奖励，未来的奖励就要把它打折扣。

• 有了 return 后，就可以定义一个状态的价值了，就是 state value function。对于 MRP，state value function 被定义成是 return 的期望，如下式所示：
  $$\begin{array}{rl}{V}_t(s)& =\mathbb{E}[G_t\mid s_t=s]\\ & =\mathbb{E}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{T-t-1}{R}_T\mid s_t=s]\end{array}$$

$G_t$ 是之前定义的 discounted return，这里取了一个期望，期望就是说从这个状态开始，你有可能获得多大的价值。所以这个期望也可以看成是对未来可能获得奖励的它的当前价值的一个表现，就是当你进入某一个状态过后，现在有多大的价值。

3.Why Discount Factor

为什么需要 discount factor：

• 有些马尔可夫过程是带环的，它并没有终结，我们想避免这个无穷的奖励。
• 我们并没有建立一个完美的模拟环境的模型，也就是说，我们对未来的评估不一定是准确的，我们不一定完全信任我们的模型，因为这种不确定性，所以我们对未来的预估增加一个折扣。我们想把这个不确定性表示出来，希望尽可能快地得到奖励，而不是在未来某一个点得到奖励。
• 如果这个奖励是有实际价值的，我们可能是更希望立刻就得到奖励，而不是后面再得到奖励（现在的钱比以后的钱更有价值）。
• 在人的行为里面来说的话，大家也是想得到即时奖励。
• 有些时候可以把这个系数设为 0，设为 0 过后，我们就只关注了它当前的奖励。我们也可以把它设为 1，设为 1 的话就是对未来并没有折扣，未来获得的奖励跟当前获得的奖励是一样的。

这个系数可以作为强化学习 agent 的一个 hyperparameter（超参数） 来进行调整，然后就会得到不同行为的 agent。

仍然是上图的MRP示例，接下来讨论如何计算价值：
我们现在可以计算每一个轨迹得到的奖励，比如我们对于这个 $s_4,s_5,s_6,s_7$ 轨迹的奖励进行计算，这里折扣系数是 0.5。

• 在 $s_4$ 的时候，奖励为零。
• 下一个状态 $s_5$ 的时候，要把 $s_5$ 进行一个折扣，$s_5$ 本身也是没有奖励的。
• 然后是到 $s_6$ ，也没有任何奖励，折扣系数应该是 $\frac{1}{4}$ 。
• 到达 $s_7$ 后，获得了一个奖励，但是因为 $s_7$ 这个状态是未来才获得的奖励，所以要进行三次折扣。

所以对于这个轨迹，它的 return 就是 1.25，类似地，可以得到其它轨迹的 return 。

当有了一些轨迹的 return 后，可以通过产生从当前位置出发的所有轨迹取平均的方法来获取前进到当前位置的价值。此即蒙特卡罗采样算法。

4.Bellman Equation

但是这里我们采取了另外一种计算方法，我们从价值函数里面推导出 Bellman Equation（贝尔曼等式），如下式所示：$$V(s)=\underset{\mathrm{I}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}{R_s}+\underset{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{s}\mathrm{u}\mathrm{m}\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}{\gamma \sum _{s^{\prime }\in S}P(s^{\prime }\mid s)V(s^{\prime })}$$

其中：

• s’ 可以看成未来的所有状态。
• 转移 P(s’|s) 是指从当前状态转移到未来状态的概率。
• 第二部分可以看成是一个 Discounted sum of future reward。
• V(s’) 代表的是未来某一个状态的价值。我们从当前这个位置开始，有一定的概率去到未来的所有状态，所以我们要把这个概率也写上去，这个转移矩阵也写上去，然后我们就得到了未来状态，然后再乘以一个 γ，这样就可以把未来的奖励打折扣。

即当前状态的价值是当前状态的即时价值和未来价值期望（$\sum$(向各个状态的转移概率×对应状态的价值)）× γ 。

Bellman Equation 定义了当前状态跟未来状态之间的关系。未来打折扣的奖励加上当前立刻可以得到的奖励，就组成了这个 Bellman Equation。 当前状态的值函数可以通过下个状态的值函数来计算。

可以将 Bellman equation 写成矩阵的形式：

可以将矩阵形式的 Bellman equation 转化成下列形式：
$$\begin{array}{rl}V& =R+\gamma PV\\ IV& =R+\gamma PV\\ (I-\gamma P)V& =R\\ V& ={(I-\gamma P)}^{-1}R\end{array}$$

从而可以得到一个解析解：
$$V={(I-\gamma P)}^{-1}R$$

由此，可以通过矩阵求逆直接将价值 V 求出，但矩阵求逆的复杂度是 $O(N^3)$ ，所以这种通过解析解去求解的方法只适用于小量的 MRP。

5.Iterative Algorithm for Computing Value of a MRP

Bellman equation 只能解决小量的 MRP ，对于状态很多的 MRP ，可以通过迭代的方法来解：

• 动态规划的方法
• 蒙特卡罗的办法（通过采样的办法去计算它）
• Temporal-Difference Learning 的办法。 Temporal-Difference Learning 叫 TD Leanring，它是动态规划和蒙特卡罗的一个结合

（1）蒙特卡罗方法

蒙特卡罗(Monte Carlo)方法就是以当前状态为起点，遍历大量可能轨迹，得到对应的大量 return 。将得到的大量 return 取平均，作为当前状态的价值。

比如说我们要算 $s_4$ 状态的一个价值。我们就可以从 $s_4$ 状态开始，随机产生很多轨迹。每个轨迹，我们可以算到它的 return。每个轨迹都会得到一个 return，从而得到大量的 return 。比如说一百个、一千个的 return ，然后直接取一个平均，那么就可以等价于现在 $s_4$ 价值，因为 $s_4$ 的价值 $V(s_4)$ 定义了你未来可能得到多少的奖励。

（2）动态规划

也可以用动态规划的办法，一直迭代 Bellman equation，让它最后收敛，就可以得到它的状态。所以算法二就是一个迭代的算法，通过 bootstrapping(拔靴自助) 的办法，然后去不停地迭代这个 Bellman Equation。当这个最后更新的状态跟你上一个状态变化并不大的时候，更新就可以停止，我们就可以输出最新的 V’(s) 作为它当前的状态。所以这里就是把 Bellman Equation 变成一个 Bellman Update，这样就可以得到价值。

动态规划的方法基于后继状态值的估计来更新状态值的估计（算法二中的第 3 行用 V’ 来更新 V ）。也就是说，它们根据其他估算值来更新估算值。我们称这种基本思想为 bootstrapping。

---

上一篇：强化学习RL学习笔记3-gym了解与coding实践
下一篇：强化学习RL学习笔记5-马尔可夫决策过程（MDP）(2)