Weisfeiler-Lehman 算法
很多论文中会讲,从另一个角度来讲,GCN模型可以看作图上非常有名的 Weisfeiler-Lehman 算法的一种变形。那么什么是 Weisfeiler-Lehman 算法呢?
一维的 Weisfeiler-Lehman 如下所示:
下面举例说明 Wisfeiler-Lehman 算法
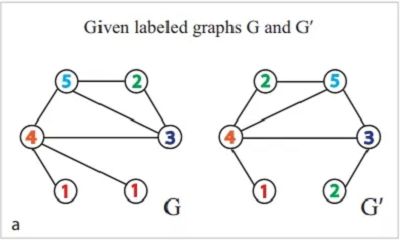
给定两图 $G$ 和 $G^{\prime}$,其中每个节点都已经打上了标签(实际应用中,有些时候我们并拿不到节点的标签, 这时可以对节点都标上 "1" 这个标签)
要比较 $\mathrm{G}$ 和 $\mathrm{G}^{\prime}$ 的相似性,我们来看看 weisfeiler-lehman 算法是怎么做的:
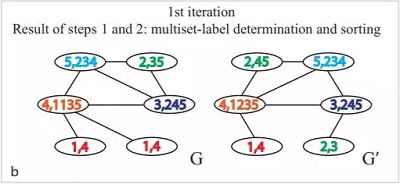
1、aggregate 邻居节点的标签得到一个标签的字符串,对字符串进行升序排列。
2、对字符串进行哈希处理,这里生成了一个一一映射的字典,这一步也可以使用其它的字符串哈希函数,只要保证碰撞率尽量小就可以。
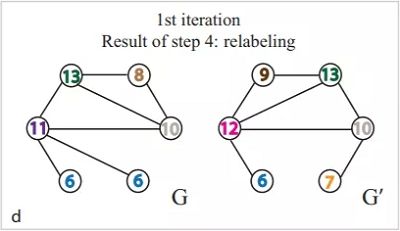
3. 将哈希过的值重新赋值给相应的节点
这样第一轮迭代之后, $G=\{6 、 6 、 8 、 10 、 11 、 13\} $, $G^{\prime}=\{6 , 7 , 9 , 10 , 12 , 13\}$ 于是利用 Jaccard 公 式就可以计算出 $G$ 和 $G$ 的相似度了,如果需要更严格的对比,可以持续迭代上述过程。
Jaccard系数
Jaccard index , 又称为 Jaccard 相似系数(Jaccard similarity coefficient)用于比较有限样本集之间的相似性与差异性。Jaccard 系数值越大,样本相似度越高。
定义:给定两个集合A,B,Jaccard 系数定义为A与B交集的大小与A与B并集的大小的比值,定义如下:
$J(A, B)=\frac{|A \cap B|}{|A \cup B|}=\frac{|A \cap B|}{|A|+|B|-|A \cap B|}$
当集合 A,B 都为空时,J(A,B) 定义为 1。
与Jaccard 系数相关的指标叫做Jaccard 距离,用于描述集合之间的不相似度。Jaccard 距离越大,样本相似度越低。公式定义如下:
$d_{j}(A, B)=1-J(A, B)=\frac{|A \cup B|-|A \cap B|}{|A \cup B|}=\frac{A \Delta B}{|A \cup B|}$
其中对称差(symmetric difference)$A \Delta B=|A \cup B|-|A \cap B|$ 。
性质:$J(A, B) \in[0,1]$