机器学习手写多层神经网络实现猫的识别
本文基于吴恩达老师深度学习作业,用多层神经网络实现猫的识别。
-
-
- 准备第三方库
- 加载数据
- 查看数据
- 测试结果
- 先定义前向传播中的线性部分
- 线性激活部分
- 用交叉熵损失函数计算代价
- 定义sigmoid和Relu激活函数反向传播部分
- 完整反向传播函数
- 反向传播模型
- 更新参数
- 多层神经网络模型
- 开始训练
- 训练结果
- 用训练好的参数预测自己的图片
-
我们来说一下步骤:
初始化网络参数
前向传播
1 计算一层的中线性求和的部分
2计算激活函数的部分(ReLU使用L-1次,Sigmod使用1次)
3 结合线性求和与激活函数
计算误差
反向传播
1 线性部分的反向传播公式
2 激活函数部分的反向传播公式
3 结合线性部分与激活函数的反向传播公式
更新参数
准备第三方库
# 导入必要库
import numpy as np
import h5py
import scipy
from scipy import ndimage
import matplotlib.pyplot as plt
import testCases
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward #参见资料包
import lr_utils
加载数据
数据来自吴恩达深度学习周四课程中的猫的图片数据
# 加载数据
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()
train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y
查看数据
index = 25
plt.imshow(train_set_x_orig[25]) #查看第26张图片
print(train_set_y) # 查看所有标签,1 猫 0 不是猫
[[0 0 1 0 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 0
0 0 1 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 1 1 0 1 1 1 0 0 0 0 0 0 1 0 0 1
0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 1 0 0 0 0 1 0 1 0 1 1
1 1 1 1 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0
1 1 1 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 1 1 1 0 0 1 1 0 1 0 1
0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0]]
# 初始化神经网络结构
def initialize_parameters_deep(layers_dims):
"""
此函数是为了初始化多层网络参数而使用的函数。
参数:
layers_dims - 包含我们网络中每个图层的节点数量的列表
返回:
parameters - 包含参数“W1”,“b1”,...,“WL”,“bL”的字典:
W1 - 权重矩阵,维度为(layers_dims [1],layers_dims [1-1])
bl - 偏向量,维度为(layers_dims [1],1)
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for l in range(1,L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1])
parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
#确保我要的数据的格式是正确的
assert(parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l-1]))
assert(parameters["b" + str(l)].shape == (layers_dims[l], 1))
return parameters
# 测试
initialize_parameters_deep(layers_dims = [5,4,4,1])
测试结果
{'W1': array([[ 0.79989897, 0.19521314, 0.04315498, -0.83337927, -0.12405178],
[-0.15865304, -0.03700312, -0.28040323, -0.01959608, -0.21341839],
[-0.58757818, 0.39561516, 0.39413741, 0.76454432, 0.02237573],
[-0.18097724, -0.24389238, -0.69160568, 0.43932807, -0.49241241]]),
'W2': array([[-0.59252326, -0.10282495, 0.74307418, 0.11835813],
[-0.51189257, -0.3564966 , 0.31262248, -0.08025668],
[-0.38441818, -0.11501536, 0.37252813, 0.98805539],
[-0.62206166, -0.31320846, -0.40188305, -1.20954159]]),
'W3': array([[-0.46189601, -0.51193788, 0.56198898, -0.06595712]]),
'b1': array([[0.],
[0.],
[0.],
[0.]]),
'b2': array([[0.],
[0.],
[0.],
[0.]]),
'b3': array([[0.]])}
先定义前向传播中的线性部分
# 前向传播线性部分
def linear_forward(A,W,b):
"""
实现前向传播的线性部分。
参数:
A - 来自上一层(或输入数据)的激活,维度为(上一层的节点数量,示例的数量)
W - 权重矩阵,numpy数组,维度为(当前图层的节点数量,前一图层的节点数量)
b - 偏向量,numpy向量,维度为(当前图层节点数量,1)
返回:
Z - 激活功能的输入,也称为预激活参数
cache - 一个包含“A”,“W”和“b”的字典,存储这些变量以有效地计算后向传递
"""
Z = np.dot(W,A) + b
assert(Z.shape == (W.shape[0],A.shape[1]))
cache = (A,W,b)
return Z,cache
线性激活部分
def linear_activation_forward(A_prev,W,b,activation):
"""
实现LINEAR-> ACTIVATION 这一层的前向传播
参数:
A_prev - 来自上一层(或输入层)的激活,维度为(上一层的节点数量,示例数)
W - 权重矩阵,numpy数组,维度为(当前层的节点数量,前一层的大小)
b - 偏向量,numpy阵列,维度为(当前层的节点数量,1)
activation - 选择在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
A - 激活函数的输出,也称为激活后的值
cache - 一个包含“linear_cache”和“activation_cache”的字典,我们需要存储它以有效地计算后向传递
"""
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z) # return A & Z
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert(A.shape == (W.shape[0],A_prev.shape[1]))
cache = (linear_cache,activation_cache)
return A,cache
# 完整前向传播模型
def L_model_forward(X,parameters):
"""
实现[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID计算前向传播,也就是多层网络的前向传播,为后面每一层都执行LINEAR和ACTIVATION
参数:
X - 数据,numpy数组,维度为(输入节点数量,示例数)
parameters - initialize_parameters_deep()的输出
返回:
AL - 最后的激活值
caches - 包含以下内容的缓存列表:
linear_relu_forward()的每个cache(有L-1个,索引为从0到L-2)
linear_sigmoid_forward()的cache(只有一个,索引为L-1)
"""
caches = []
A = X
L = len(parameters) // 2
# 前L-1层使用Relu激活函数,最后一层使用sigmoid激活函数
for l in range(1,L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
caches.append(cache)
AL,cache = linear_activation_forward(A, parameters['W'+str(L)], parameters['b'+str(L)], "sigmoid")
caches.append(cache)
return AL, caches
用交叉熵损失函数计算代价
# 计算成本
def compute_cost(AL,Y):
"""
参数:
AL - 与标签预测相对应的概率向量,维度为(1,示例数量)
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
返回:
cost - 交叉熵成本
"""
m = Y.shape[1]
cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m
cost = np.squeeze(cost)
assert(cost.shape == ())
return cost
# 反向传播的线性部分
def linear_backward(dZ,cache):
"""
为单层实现反向传播的线性部分(第L层)
参数:
dZ - 相对于(当前第l层的)线性输出的成本梯度
cache - 来自当前层前向传播的值的元组(A_prev,W,b)
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度,与W的维度相同
db - 相对于b(当前层l)的成本梯度,与b维度相同
"""
A_prev, W, b = cache
m = A_prev.shape[1]
dW = np.dot(dZ, A_prev.T) / m
db = np.sum(dZ, axis=1, keepdims=True) / m
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
定义sigmoid和Relu激活函数反向传播部分
def sigmoid_backward(dA, cache):
Z = cache
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1-s)
assert (dZ.shape == Z.shape)
return dZ
def relu_backward(dA, cache):
Z = cache
dZ = np.array(dA, copy=True) # just converting dz to a correct object.
dZ[Z <= 0] = 0
assert (dZ.shape == Z.shape)
return dZ
完整反向传播函数
def linear_activation_backward(dA,cache,activation="relu"):
"""
实现LINEAR-> ACTIVATION层的后向传播。
参数:
dA - 当前层l的激活后的梯度值
cache - 我们存储的用于有效计算反向传播的值的元组(值为linear_cache,activation_cache)
activation - 要在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度值,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度值,与W的维度相同
db - 相对于b(当前层l)的成本梯度值,与b的维度相同
"""
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev,dW,db
反向传播模型
def L_model_backward(AL,Y,caches):
"""
对[LINEAR-> RELU] *(L-1) - > LINEAR - > SIGMOID组执行反向传播,就是多层网络的向后传播
参数:
AL - 概率向量,正向传播的输出(L_model_forward())
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
caches - 包含以下内容的cache列表:
linear_activation_forward("relu")的cache,不包含输出层
linear_activation_forward("sigmoid")的cache
返回:
grads - 具有梯度值的字典
grads [“dA”+ str(l)] = ...
grads [“dW”+ str(l)] = ...
grads [“db”+ str(l)] = ...
"""
grads = {}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L-1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, "sigmoid")
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
更新参数
def update_parameters(parameters, grads, learning_rate):
"""
使用梯度下降更新参数
参数:
parameters - 包含你的参数的字典
grads - 包含梯度值的字典,是L_model_backward的输出
返回:
parameters - 包含更新参数的字典
参数[“W”+ str(l)] = ...
参数[“b”+ str(l)] = ...
"""
L = len(parameters) // 2 #整除
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
多层神经网络模型
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False,isPlot=True):
"""
实现一个L层神经网络:[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID。
参数:
X - 输入的数据,维度为(n_x,例子数)
Y - 标签,向量,0为非猫,1为猫,维度为(1,数量)
layers_dims - 层数的向量,维度为(n_y,n_h,···,n_h,n_y)
learning_rate - 学习率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每100次打印一次
isPlot - 是否绘制出误差值的图谱
返回:
parameters - 模型学习的参数。 然后他们可以用来预测。
"""
np.random.seed(1)
costs = []
parameters = initialize_parameters_deep(layers_dims)
for i in range(0,num_iterations):
AL , caches = L_model_forward(X,parameters)
cost = compute_cost(AL,Y)
grads = L_model_backward(AL,Y,caches)
parameters = update_parameters(parameters,grads,learning_rate)
#打印成本值,如果print_cost=False则忽略
if i % 100 == 0:
#记录成本
costs.append(cost)
#是否打印成本值
if print_cost:
print("第", i ,"次迭代,成本值为:" ,np.squeeze(cost))
#迭代完成,根据条件绘制图
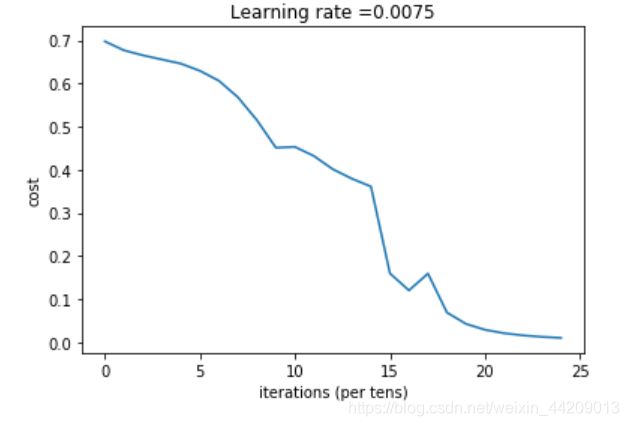
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
# 预测函数
def predict(X, y, parameters):
"""
该函数用于预测L层神经网络的结果,当然也包含两层
参数:
X - 测试集
y - 标签
parameters - 训练模型的参数
返回:
p - 给定数据集X的预测
"""
m = X.shape[1]
n = len(parameters) // 2 # 神经网络的层数
p = np.zeros((1,m))
#根据参数前向传播
probas, caches = L_model_forward(X, parameters)
for i in range(0, probas.shape[1]):
if probas[0,i] > 0.5:
p[0,i] = 1
else:
p[0,i] = 0
print("准确度为: " + str(float(np.sum((p == y))/m)))
return p
开始训练
layers_dims = [12288, 5, 5, 5, 1] # 神经网络结构
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True,isPlot=True)
训练结果
第 0 次迭代,成本值为: 0.6978343828561023
第 100 次迭代,成本值为: 0.677132430616011
第 200 次迭代,成本值为: 0.6654901610560577
第 300 次迭代,成本值为: 0.6558182563579574
第 400 次迭代,成本值为: 0.6462338773043887
第 500 次迭代,成本值为: 0.629556239504452
第 600 次迭代,成本值为: 0.6064716676762193
第 700 次迭代,成本值为: 0.5682128757590694
第 800 次迭代,成本值为: 0.5150993982487242
第 900 次迭代,成本值为: 0.45119773439072314
第 1000 次迭代,成本值为: 0.45320425106544443
第 1100 次迭代,成本值为: 0.43195959636341597
第 1200 次迭代,成本值为: 0.4011698565079565
第 1300 次迭代,成本值为: 0.3792819244178975
第 1400 次迭代,成本值为: 0.3612456937302191
第 1500 次迭代,成本值为: 0.15978415024822354
第 1600 次迭代,成本值为: 0.12024692222669645
第 1700 次迭代,成本值为: 0.15938383021735222
第 1800 次迭代,成本值为: 0.06896835915402598
第 1900 次迭代,成本值为: 0.04264941082744414
第 2000 次迭代,成本值为: 0.029008712045154702
第 2100 次迭代,成本值为: 0.021005467409719286
第 2200 次迭代,成本值为: 0.015947431793655677
第 2300 次迭代,成本值为: 0.012568847909837035
第 2400 次迭代,成本值为: 0.010198826192851727
predictions_train = predict(train_x, train_y, parameters) #训练集
predictions_test = predict(test_x, test_y, parameters) #测试集
准确度为: 1.0
准确度为: 0.76
用训练好的参数预测自己的图片
my_image = "1.jpg"
my_label_y = [1]
## END CODE HERE ##
fname = "测试图片/" + my_image
image = np.array(scipy.ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64)).reshape((64*64*3,1))
my_predicted_image = predict(my_image, my_label_y, parameters)
plt.imshow(image)
print ("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
准确度为: 1.0
y = 1.0, your L-layer model predicts a "cat" picture.