Python数据结构与算法中的栈详解(2)

目录

• 匹配括号
• 匹配符号
• 总结

匹配括号

接下来，我们使用栈解决实际的计算机科学问题。​

比如我们都写过这样所示的算术表达式， ( 5 + 6 ) ∗ ( 7 + 8 ) / ( 4 + 3 ) (5 + 6) * (7 + 8) / (4 + 3) (5+6)∗(7+8)/(4+3)，其中的括号用来改变计算顺序，或提升运算优先级。​

匹配括号是指每一个左括号都有与之对应的一个右括号，并且括号对有正确的嵌套关系。

• 正确的嵌套关系： ( ( ) ( ) ( ) ( ) ) (()()()()) (()()()())、 ( ( ( ( ) ) ) ) (((()))) (((())))、 ( ( ) ( ( ( ) ) ( ) ) ) (()((())())) (()((())()))
• 错误的嵌套关系： ( ( ( ( ( ( ( ) ) ((((((()) ((((((())、 ( ) ) ) ())) ()))

​我们的挑战就是编写一个算法，它从左到右读取一个括号串(不包括其他数字与运算符)，然后判断其中的括号是否匹配。​

为了解决这个问题， 需要注意到一个重要现象。当从左到右处理括号时，最右边的无匹配左括号必须与接下来遇到的第一个右括号相匹配。并且，在第一个位置的左括号可能要等到处理至最后一个位置的右括号时才能完成匹配。而且右括号的出现顺序，与其相匹配的左括号的出现顺序相反。这一规律暗示着能够运用栈来解决括号匹配问题。

一旦认识到用栈来保存括号，算法编写起来就会十分容易。​

由一个空栈开始，从左往右依次处理括号。如果遇到左括号，便通过栈的push操作将其加入栈中，以此表示稍后需要有一个与之匹配的右括号。

反之，如果遇到右括号，就调用栈的pop操作。只要栈中的所有左括号都能遇到与之匹配的右括号，那么整个括号串就是匹配的；如果栈中有任何一个左括号找不到与之匹配的右括号，则括号串就是不匹配的。在处理完匹配的括号串之后，栈应该是空的。​

用简单的话说就是：扫描括号串，左括号入栈，遇见右括号，从栈顶取出来一个左括号配对儿，互相抵消，直到最后。如果括号匹配，那么栈最后就该是空的，并且括号串刚好扫描完毕。

代码实现如下：

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()

def parChecker(symbolString):
    s = Stack()  # 构造栈
    balanced = True  # 匹配标志 默认为True 表示匹配
    index = 0  # 索引 用来取字符
    # 当 索引小于字符串的长度 并且 匹配标志为True 时
    while index < len(symbolString) and balanced:
        # 取字符串当前位的字符
        symbol = symbolString[index]
        # 如果当前字符为 左括号 则入栈
        if symbol == '(':
            s.push(symbol)
        # 如果当前字符 不是左括号(那当前就是右括号)
        else:
            # 并且栈是空的
            if s.isEmpty():
                # 匹配标志设置为 False 表示匹配失败(孤零零的右括号)
                balanced = False
            # 栈不是空的 抵消栈顶的左括号
            else:
                s.pop()
        # 索引向后移动一位
        index = index + 1
    # 循环结束 如果匹配成功 并且 栈空了
    if balanced and s.isEmpty():
        return True
    else:
        return False

注意，balanced 的初始值是True，这是因为一开始没有任何理由假设其为False 。如果当前的符号是左括号，它就会被压入栈中（第27行）。注意第36行，仅通过pop()将一个元素从栈顶移除。由于移除的元素一定是之前遇到的左括号，因此并没有用到pop()的返回值。在第42~45行， 只要所有括号匹配并且栈为空，函数就会返回True ，否则返回False。​

匹配符号

符号匹配是许多编程语言中的常见问题，括号匹配问题只是它的一个特例。我们已经会了匹配括号的方法，那么现在我们来试试匹配符号。​

匹配符号是指正确地匹配和嵌套左右对应的符号。​

例如，在Python中，方括号“[”和“]”用于列表；花括号“{”和“}”用于字典；括号“(”和“)”用于元组和算术表达式。只要保证左右符号匹配，就可以混用这些符号。以下符号串是匹配的，其中不仅每一个左符号都有一个右符号与之对应，而且两个符号的类型也是一致的。

• { { ( [ ] [ ] ) } ( ) }
• [ [ { { ( ( ) ) } } ] ]
• [ ] [ ] [ ] ( ) { }

​以下符号则是不匹配的：

• ( [ ) ]
• ( ( ( ) ] ) )
• [ { ( ) ]

​要处理新类型的符号，我们扩展上面的括号匹配检测代码。​

即每一个左符号都将被压入栈中，以待之后出现对应的右符号。​

唯一的区别在于，当出现右符号时，必须先检测其类型是否与栈顶的左符号类型相匹配。如果两个符号不匹配，那么整个符号串也就不匹配。同样，如果整个符号串处理完成并且栈是空的，那么就说明所有符号正确匹配。

代码实现如下：

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()

def parChecker(symbolString):
    s = Stack()  # 构造栈
    balanced = True  # 匹配标志 默认为True 表示匹配
    index = 0  # 索引 用来取字符
    # 当 索引小于字符串的长度 并且 匹配标志为True 时
    while index < len(symbolString) and balanced:
        # 取字符串当前位的字符
        symbol = symbolString[index]
        # 如果当前字符属于 左括号集 则入栈
        if symbol in '([{':
            s.push(symbol)
        # 如果当前字符 不是左括号(那当前就是右括号)
        else:
            # 并且栈是空的
            if s.isEmpty():
                # 匹配标志设置为 False 表示匹配失败(孤零零的右括号)
                balanced = False
            # 栈不是空的 拿出栈顶的左括号进行类型匹配
            else:
                top = s.pop()
                # 类型匹配失败
                if not matches(top, symbol):
                    balanced = False
        # 索引向后移动一位
        index = index + 1
    # 循环结束 如果匹配成功 并且 栈空了
    if balanced and s.isEmpty():
        return True
    else:
        return False

def matches(left, right):
    lefts = "([{"
    rights = ")]}"
    # 调用字符串的index方法，index() 方法查找指定值的首次出现，并返回索引。
    # 左右索引对应，表明符号匹配
    return lefts.index(left) == rights.index(right)

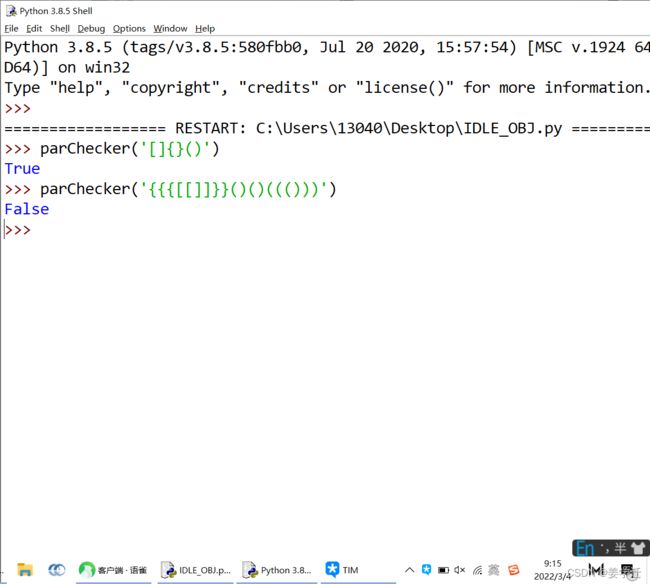
测试结果如下图所示：

以上两个例子说明，在处理编程语言的语法结构时，栈是十分重要的数据结构。几乎所有记法都有某种需要正确匹配和嵌套的符号。除此之外，栈在计算机科学中还有其他一些重要的应用场景，让我们继续探索。

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注脚本之家的更多内容!