在Seal库和HElib库中都用到了NTT技术,用于加快多项式计算,而NTT又是FFT的优化,FFT又来自于DFT,现在具体学习一下这三个技术!
基础概念
名词区分
1、DFT:离散傅立叶变换
2、FFT:快速傅立叶变换
3、NTT:快速数论变换
4、MTT:NTT的扩展
5、多项式卷积:多项式乘法
6、根据多项式的系数表示法求点值表示法的过程叫做“求值”;根据点值表示法求系数表示法的过程称为“插值”
7、求一个多项式的乘法,即求卷积,先通过傅立叶变换对系数表示法的多项式进行求值运算,其复杂度\(O(nlog^n)\),然后在\(O(n)\)的时间内点值相乘,在进行插值运算。

8、如果选取单位复根作为求值点,则可以对系数向量进行离散傅立叶变换(DFT),得到相应的点值表示;同样可以通过对点值进行逆DFT运算,获得相应的系数向量。DFT和逆DFT时间复杂度均为\(O(nlog^n)\)。
复数
定义
我们知道,一个复数可以这样表示:\(a+bi\),a和b是实数,其中\(i\)叫做虚数单位,复数域是目前已知最大的域。
在复平面中,x轴代表实数,y轴(除原点外的点)代表虚数,从原点(0,0)到(a,b)的向量表示复数\(a+bi\)
模长:从原点(0,0)到(a,b)的距离,即\(\sqrt{a^2+b^2}\)
幅角:假设以逆时针为正方向,从x轴正半轴到已知向量的转角的有向角叫做幅角

运算
1、加法
在复数平面,复数可以表示为向量,因为复数的加法和向量的加法相同。
2、乘法
几何定义:复数相乘密,模长相乘,幅角相加
代数定义:
单位根
在复数平面上,以原点为圆心,1为半径做圆,所得的圆叫做单位圆,以圆点为起点,圆的n等分为终点,做n个向量,设幅角为正且最小的向量对应的复数为w_n$,称为n次单位根。
根据复数乘法的运算法则,其余n-1个复数为\(w_n^2,...,w_n^n\),注意\(w_n^0=w_n^n=1\)(对应复平面上以x轴为正方向的向量)
如何计算呢?
由欧拉公式解决\(w_n^k=cos(k*2\pi/n)+isin(k*2\pi/n)\)
例如:向量AB表示的是复数为4次单位根

n次单位根的幅角为周角的\(1/n\)。
在代数中,若\(z_n=1\),我们把z称为n次单位根。具体请参考:n次单位根(n-th unit root)
单位根的性质
1、\(w_n^k=cos(k*2\pi/n)+isin(k*2\pi/n)\)
2、【相消引理】\(w_{dn}^{dk}=w_n^k\)
证明:以d=2为例

3、【折半引理】\(w_n^{k+n/2}=-w_n^k\)
证明:

4、\(w_n^0=w_n^k=1\)
5、\(w_n^{n-i} = 共轭(w_n^i)\)
6、\(w_n^{n+i}=w_n^i\)
多项式系数表示法
设\(A(x)\)表示一个d次多项式,则\(A(x)=a_1+a_2*x+...,+a_{d}*x^{d}\)
利用这种方法计算多项式卷积复杂度为\(O(d^2)\),其实就是直接对应相乘(暴力)。
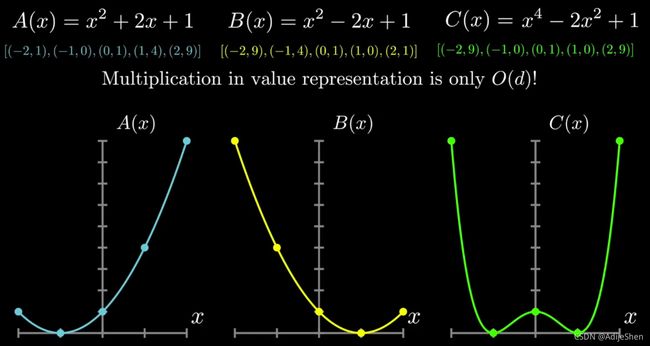
例如:\(A(x)=1+2x+x^2\), \(B(x)=1-2x+x^2\)
多项式点值表示法
将n个值x带入多项式,会得到d各不同的值y,则该多项式被这n个点值\((x_1,y_1),...,(x_d,y_x)\)唯一确定,其中\(\sum_{j=1}^{d}a_j*x^j_i\)
而利用点值法计算多项式卷积复杂度也为\(O(d^2)\)。(选点\(O(d)\),每次计算\(O(d)\))
例如上面的多项式用点值法表示:\(A(x)=[(-2,1),(-1,0),(0,1),(1,4),(2,9)],B(x)=[(-2,9),(-1,4),(0,1),(1,0),(2,1)]\),则
即有这个5个点就可以唯一确定一个4次多项式,而两两相乘的复杂度为\(O(d)\)
引理1:\(( d + 1 )\)个点值可以唯一确定一个d 阶多项式
因此,我们可以将一个系数多项式转换为一个点值多项式,然而进行复杂度为\(O(d)\)的乘法,再将结果的点值多项式恢复回系数多项式。

但是:如果我们采用下面这种矩阵形式计算点值的话【选点】,那么由系数转为点值的复杂度也为\(O(d^2)\)。

接下来考虑对其优化:
1、对于系数表示法,每个点的系数都固定,优化困难
2、对于点值表示法,可以用FFT来解决!
DFT
已知\(A(x)\)的系数为\((a_0,a_1,...,a_{n-1})\),对于\(k=0,1,...,n-1\),定义:
其中向量\(y=(y_0,y_1,...,y_{n-1})\)是系数向量\(a=(a_0,a_1,...,a_{n-1})\)的离散傅立叶变换,记\(y=DFT_n(a)\),复杂度为\(O(n^2)\)
而使用下面的FFT方法,可以在\(O(nlog^n)\)时间内求出\(DFT_n(a)\)

FFT
用于加速系数多项式到点值多项式的运算!
首先观察下面多项式:

例如:\(F(x)=x^2\),有对称性\(F(-x)=F(x)\),相当于确定了一个点相当于确定两个点。
同理又如\(F(x^3)\),有性质\(F(-x)=-F(x)\),也是确定了一个点相当于确定了两个点。
所以对于有奇偶行的多项式,只需要找到原本一半的点就可以得到这个多现实了。
基于以上想法,假如有下面多项式:

把\(P_e\)和\(P_o\)分别看作两个多项式,也就是对于一个点\(x_i\),我们只要计算出\(P_e(x_i^2)\)和\(P_o(x_i^2)\),就可以得到\(P(x_i)\)和\(P(-x_i)\),而且\(P_e\)和\(P_o\)还可以进一步拆分为奇偶两部分!
假设原本我们需要n个点\(【\pm x_1,\pm x_12,...,\pm x_{n/2}】\)就能确定一个\(n-1\)阶的多项式。现在变成了求\(P_e(x)\)和\(P_o(x)\)在\(x_1^2,x_2^2,...,x_{n/2}^2\)上面的点值【n/2个点】。
那如果这n/2个点两两之间满足\(x_i^2=-x_j^2\),则就可以进一步拆分为一半了,就可以将原本的复杂度\(O(d^2)\)降为\(O(dlog^d)\)。这里可以看出FFT用到了分治思想。

问题是,$x_12,x_22,...,x_{n/2}^2并不满足两两互为相反数。由此使用n次单位根,选用n个n次单文根
可以看出,将以一个n个点的求值问题转换为求n/2个点,在转换为求n/4个点,以此迭代,从而达到\(O(dlog^d)\)。将上述思想转换为为代码如下:

FFT的逆
如何从点值多项式变为系数多项式呢?
对于点值计算,
![]()
其中中间的范德蒙德矩阵就成了一个DFT矩阵。
有了正向(系数到点值)的矩阵变换,求逆向(点值到系数)就是对上面矩阵求逆即可:

从上面可以看出,FFT是将\(w\)作为点值传入,IFFT就是将\({1/n}*w^{-1}\)作为点值传入:

程序
下面程序用FFT计算两个大数乘
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1402
#include
#include
#include
#include
using namespace std;
const int N = 500005;
const double PI = acos(-1.0);
struct Virt
{
double r, i;
Virt(double r = 0.0,double i = 0.0)
{
this->r = r;
this->i = i;
}
Virt operator + (const Virt &x)
{
return Virt(r + x.r, i + x.i);
}
Virt operator - (const Virt &x)
{
return Virt(r - x.r, i - x.i);
}
Virt operator * (const Virt &x)
{
return Virt(r * x.r - i * x.i, i * x.r + r * x.i);
}
};
//雷德算法--倒位序
void Rader(Virt F[], int len)
{
int j = len >> 1;
for(int i=1; i> 1;
while(j >= k)
{
j -= k;
k >>= 1;
}
if(j < k) j += k;
}
}
//FFT实现
void FFT(Virt F[], int len, int on)
{
Rader(F, len);
for(int h=2; h<=len; h<<=1) //分治后计算长度为h的DFT
{
Virt wn(cos(-on*2*PI/h), sin(-on*2*PI/h)); //单位复根e^(2*PI/m)用欧拉公式展开
for(int j=0; j=0; i--)
{
if(result[i])
{
high = i;
break;
}
}
for(int i=high; i>=0; i--)
printf("%d",result[i]);
puts("");
}
int main()
{
while(~scanf("%s%s",str1,str2))
{
Init(str1,str2);
Work();
Export();
}
return 0;
}
NTT
在FFT中,我们需要用到复数,复数虽然很神奇,但是它也有自己的局限性——需要用double类型计算,精度太低,那有没有什么东西能够代替复数且解决精度问题呢?
这个东西,叫原根
阶
若a,p互素,且p>1,对于\(a^n mod p =1\)满足最小的n,叫做a模p的阶,记\(\delta _p(a)\).
例如:
其中:
\(2^1 mod 7 =2\)
\(2^2 mod 7 =4\)
\(2^3 mod 7 =1\)
原根
设p是正整数,a是整数,若\(\delta _p(a)\)等于\(\phi(p)\),则a为模p的一个原根。
例如:
\(\delta _7(3)=6=\phi (7)\),所以3是模7的一个原根。
原根的个数不唯一
1、若模数p有原根,那么它一定有\(\phi(\phi(p))个原根\)
2、若p为素数,原根一定存在,假设g是P的一个原根,那么\(g^i mod p (1
简单的说,就是
3、那如何求一个质数的原根呢?
对于指数p,\(p_i\)是p-1的因子,若\(g^{{p-1}/p_i} (mod p)\)恒成立,则g是p的原根。
下面就是为什么原根可以代替单位根计算?
因为原根具有和单位根相同的性质,FFT中,用到了单位根的四条性质,原根也满足这四条性质:

最终可以得到:
然后只需将FFT中的\(w_n\)替换掉,就是NTT。即:

综上,NTT的变换为:

这里P是素数且N必须是P-1的因子;由于N是2的方幂,所以可构造\(P=c.2^k+1\)的素数。
通常p取998244353,它的原根为3。
程序
使用NTT,计算两个大数乘
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 1 << 18;
const int P = (479 << 21) + 1;
const int G = 3;
const int NUM = 20;
LL wn[NUM];
LL a[N], b[N];
char A[N], B[N];
LL quick_mod(LL a, LL b, LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
void GetWn()
{
for(int i = 0; i < NUM; i++)
{
int t = 1 << i;
wn[i] = quick_mod(G, (P - 1) / t, P);
}
}
void Prepare(char A[], char B[], LL a[], LL b[], int &len)
{
len = 1;
int L1 = strlen(A);
int L2 = strlen(B);
while(len <= 2 * L1 || len <= 2 * L2) len <<= 1;
for(int i = 0; i < len; i++)
{
if(i < L1) a[i] = A[L1 - i - 1] - '0';
else a[i] = 0;
if(i < L2) b[i] = B[L2 - i - 1] - '0';
else b[i] = 0;
}
}
void Rader(LL a[], int len)
{
int j = len >> 1;
for(int i = 1; i < len - 1; i++)
{
if(i < j) swap(a[i], a[j]);
int k = len >> 1;
while(j >= k)
{
j -= k;
k >>= 1;
}
if(j < k) j += k;
}
}
void NTT(LL a[], int len, int on)
{
Rader(a, len);
int id = 0;
for(int h = 2; h <= len; h <<= 1)
{
id++;
for(int j = 0; j < len; j += h)
{
LL w = 1;
for(int k = j; k < j + h / 2; k++)
{
LL u = a[k] % P;
LL t = w * a[k + h / 2] % P;
a[k] = (u + t) % P;
a[k + h / 2] = (u - t + P) % P;
w = w * wn[id] % P;
}
}
}
if(on == -1)
{
for(int i = 1; i < len / 2; i++)
swap(a[i], a[len - i]);
LL inv = quick_mod(len, P - 2, P);
for(int i = 0; i < len; i++)
a[i] = a[i] * inv % P;
}
}
void Conv(LL a[], LL b[], int n)
{
NTT(a, n, 1);
NTT(b, n, 1);
for(int i = 0; i < n; i++)
a[i] = a[i] * b[i] % P;
NTT(a, n, -1);
}
void Transfer(LL a[], int n)
{
int t = 0;
for(int i = 0; i < n; i++)
{
a[i] += t;
if(a[i] > 9)
{
t = a[i] / 10;
a[i] %= 10;
}
else t = 0;
}
}
void Print(LL a[], int n)
{
bool flag = 1;
for(int i = n - 1; i >= 0; i--)
{
if(a[i] != 0 && flag)
{
//使用putchar()速度快很多
putchar(a[i] + '0');
flag = 0;
}
else if(!flag)
putchar(a[i] + '0');
}
puts("");
}
int main()
{
GetWn();
//71992652622957199265262295622895175513333762898450963102326778447440803476281886006800109449932463374706102636321647845385139107625719926526229571992652622956228951755133337628984509631023267784474408034762818860068001094499324633747061026363216478453851391076257199265262295719926526229562289517551333376289845096310232677844744080347628188600680010944993246337470610263632164784538513910762571992652622957199265262295622895175513333762898450963102326778447440803476281886006800109449932463374706102636321647845385139107625719926526229571992652622956228951755133337628984509631023267784474408034762818860068001094499324633747061026363216478453851391076257199265262295719926526229562289517551333376289845096310232677844744080347628188600680010944993246337470610263632164784538513910762571992652622957199265262295622895175513333762898450963102326778447440803476281886006800109449932463374706102636321647845385139107625
while(scanf("%s %s", A, B) != EOF)
{
int len;
clock_t start_time = clock();//计时开始
Prepare(A, B, a, b, len);
Conv(a, b, len);
Transfer(a, len);
cout << "elapsed time:" << 1000*double(clock() - start_time) / CLOCKS_PER_SEC
<< 'ms' << endl;
Print(a, len);
}
return 0;
}
输出:elapsed time:3.9328019
MTT
待学习!
参考
1、快速傅里叶变换(FFT)详解
2、快速数论变换(NTT)小结
3、CKKS的Encoding(CKKS方案的编码部分的笔记)
4、多项式乘法运算终极版
5、多项式乘法运算初级版