4.5 Non-Chronological Backtracking非时间顺序回溯

在发现死端后，回溯算法必须撤销先前发布的一些分支约束。在回溯的标准形式中，称为时间回溯，只有最近发布的分支约束才会被撤销。然而，按时间顺序回溯可能无法解决僵局的原因。在非时间回溯中，该算法回溯并撤销了与之关系最紧密的分支约束，该分支约束对死端负有一定的责任。在Gaschnig[48]之后，我将此过程称为回跳。

非时间回溯算法可以描述为(i)用于发现和使用nogoods进行回溯的策略和(ii)用于从nogood数据库中删除nogoods的策略的组合。

4.5.1 Backjumping

Stallman和Sussman[124]是第一个非正式地提出一种非时间回溯算法的人，这种算法称为依赖定向回溯，它发现并维护了不需要回溯的nogood。Bruynooghe[22]和Rosiers以及Bruynooghe[114]也对回跳进行了非正式的描述。第一个显式的回溯算法是由Gaschnig[48]给出的。Gaschnig的backjump算法(BJ)[48]与BT类似，只是它是从死端向后跳转的。但是，当节点的所有分支都是叶节点时，BJ只从死端节点向后跳转;否则，它将按时间顺序倒退。Dechter[34]提出了一种基于图形的回跳算法，该算法基于CSP的静态结构计算回跳点。其思想是跳到与死端变量共享约束的最新变量。该算法也是第一个在内部死端返回的算法。

Prosser[108]提出了冲突导向的backjump算法(CBJ)，这是Gaschnig的BJ从内部死端到backjump的推广。等价算法由Schiex、Verfaillie[118]和Ginsberg[54]独立提出并形式化。这些算法都使用了跳转nogood(定义4.5)的变体来决定从死端安全跳转到搜索树中的何处。假设回溯算法在搜索树中发现了非叶子deadend p = {b1，...，bj}。 该算法必须通过从p收回一些分支约束来回溯。 按时间顺序回溯会选择bj。 设J（p）⊆p为p的回跳nogood。 回跳选择最大的i，1≤i≤j，使得bi∈J（p）。 这是跳跃点。该算法在搜索树中向后跳转，同时撤销bi，同时撤销bi之后发布的任何分支约束，删除bi之后记录的任何nogoods。

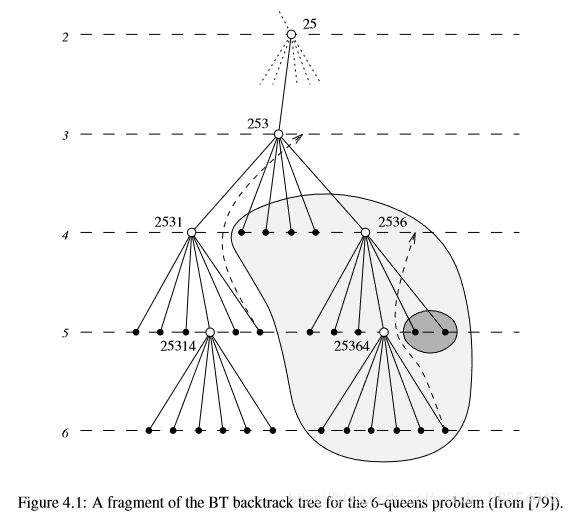
作为应用CBJ和BJ的示例，请考虑图4.1所示的回溯树。树的浅色部分包含冲突定向回跳(CBJ)跳过的节点。该算法在扩展节点25314失败后发现了一个死端。如前所述，与该节点关联的跳转是{x1 = 2,x2 = 5,x3 = 3,x5 = 4}。CBJ回滚并撤消最近发布的分支约束，即x5 = 4。此时没有跳过任何节点。x5的其余两个值也失败了。该算法现在发现，2531是一个死端节点，由于每个分支都确定了跳转nogood，所以很容易发现2531的跳转nogood为{x1 = 2,x2 = 5,x3 = 3}。CBJ向后跳转到retract x3 = 3，跳过子树的其余部分。跳远用虚线箭头表示。与CBJ不同的是，当从死端伸出的所有分支都是叶节点时，BJ只从死端向后跳转。树的暗阴影部分包含两个节点，可以通过向后跳转(BJ)跳过它们。同样，backjump由一个虚线箭头表示。

与动态回溯(dynamic backtracking, DBT)相同，当所有分支约束都是x = a形式时，对于某个变量x和值a，可以使用O(n2d)空间实现CBJ，其中n是变量的数量，d是域的大小。数据结构为每个变量和值对维护一个nogood，每个nogood的长度为O(n)。但是，由于CBJ只使用记录的nogoods进行回跳，并且从不检查或传播与nogoods对应的约束，因此没有必要为每个值实际存储nogood。更简单的O(n2)数据结构(有时称为冲突集)就足够了。冲突集为每个变量存储nogoods与该变量的每个值的并集。

CBJ还与约束传播相结合。对于所有执行非时间回溯的算法，无论执行何种级别的约束传播，基本的回溯机制都是相同的。主要区别在于如何构造跳转nogood(参见4.4.1节和定义4.7)。Prosser[108]提出了FC-CBJ算法，该算法结合了前向检查约束传播和冲突导向的回溯。Schiex和Verfaillie独立提出并形式化的等价算法[118]。Rosiers和Bruynooghe[114]还对一种结合前向检查和后跳的算法进行了非正式描述。Prosser[109]提出了mc - cbj算法，该算法结合了保持弧一致性和冲突导向的跳变。如指定，该算法只处理二进制约束。Chen[25]将该算法推广到非二进制约束。

文献报道了许多关于冲突导向背跳的实验研究。其中许多在4.10.1节中进行了总结。

4.5.2 Partial Order Backtracking 

在按时间顺序的回溯和冲突导向的回跳中，假设搜索树中节点p = {b1，...，bj}处的分支约束是完全有序的。 总排序是通过算法发布分支约束的顺序。 按时间顺序回溯然后总是缩回bj，排序中的最后一个分支约束，并且backjumping选择最大的i，1≤i≤j，这样bi就是回跳nogood。

Bruynooghe [22]指出，这不是一个必要的假设，并提出了部分顺序回溯。 在部分排序回溯中，分支约束被认为是最初无序的，并且在从后端跳回时引起部分顺序。 假设一种d-way分支策略，其中所有分支约束都是赋值给变量。当从死端跳转回来时，必须从跳转nogood中选择一个赋值x = a并撤销。Bruynooghe注意到，回跳必须尊重当前的部分顺序，并建议在部分顺序中选择最大的赋值。在作出这个选择和倒退之后，现在必须进一步限制部分顺序。回想一下，nogood {x1 = a1，...，xk = ak}可以写成（（x1 = a1）∧···∧（xk-1 = ak-1））⇒（xk ak））。赋值x = a现在必须出现在任何出现它的nogood的右边。添加蕴涵限制了部分顺序，因为蕴涵左边的赋值必须在右边的赋值之前。如果被撤销的赋值x = a出现在任意含义的左边，这个含义就会被删除，右边的值就会恢复到它的定义域。删除暗示可以放松部分顺序。Rosiers和Bruynooghe[114]在硬(非二进制)词和问题的实验中表明，相对于进行前向检查、前跳或前向检查和后跳组合的算法，他们的部分顺序回溯算法是最佳选择。然而，Baker[7]给出了一个例子(这个例子要感谢Ginsberg)，这个例子表明，因为在Bruynooghe的方案中，可以选择部分顺序中最大值的任何赋值，所以算法可以循环而不终止。

Ginsberg提出了动态回溯算法[54](DBT，见表4.1)。DBT可以看作是Bruynooghe部分序回溯方案的形式化和校正。为了保证终止，DBT总是从跳转nogood中选择最近发布的任务，并将该任务放在含义的右侧。因此，DBT对jumpback nogood中的任务维持一个总的顺序，对jumpback nogood中的任务维持一个部分顺序。因此，如果给定相同的跳转nogood, DBT的跳转点将与CBJ相同。但是，与CBJ在回跳时撤销在回跳点之后发布的任何nogoods不同，DBT保留这些nogoods(有关DBT中使用的nogood保留策略的进一步讨论，请参见4.4.2节)。Ginsberg[54]在使用填字游戏作为测试平台的实验中表明，DBT比backjump算法在固定的时间内可以解决更多的问题。然而，Baker[7]表明，关联有界的nogood记录(如DBT中使用的那样)可以与动态变量排序启发式产生负面影响。因此，DBT还可以在不保留CBJ等任何优点的算法上以指数方式降低性能。

动态回溯(DBT)也与约束传播相结合。Jussien、Debruyne、Boizumault[75]展示了如何将DBT与前向检查和保持arc一致性相结合，分别给出FC-DBT和MAC-DBT。与向CBJ添加约束传播一样，主要区别在于如何构造跳转nogood(参见4.4.1节和定义4.7)。但是，由于nogoods的保留，在向DBT添加约束传播时存在CBJ中不存在的额外复杂性。考虑一个变量域中的值，该变量已经被删除，但是它的消除解释现在是无关紧要的。该值不能直接还原，删除的值可能存在其他相关解释;即可能存在通过约束传播来删除值的几种方法。

Ginsberg和McAllester[56]提出了一种称为部分阶动态回溯(PBT)的算法。与DBT相比，PBT在从跳转到隐含意义右侧的nogood中选择任务时提供了更多的自由，同时仍然保证了正确性和终止性。在金斯堡的DBT和Bruynooghe的偏序算法中，删除隐含可以放松偏序。在PBT中，其思想是保留来自这些已删除含义的部分排序信息。现在，选择部分顺序中最大的赋值是正确的。Bliek[18]证明了PBT不是DBT的推广，并给出了一种同时推广PBT和DBT的算法。到目前为止，还没有关于PBT或Bliek推广的系统评价的报道，也没有关于约束传播的集成的报道。