Policy-based RL小结(Policy Gradient ; Natural policy gradient ;TRPO;ACKTR;PPO )
文章目录
- Policy-based RL
-
- 前言
- 1. 预备知识
-
- 1.1 策略类型
- 1.2 策略优化的目标函数
-
- 1.2.1 可结束的环境的目标函数
- 1.2.3 连续动作环境的目标函数
- 1.2.4 实际的目标函数的定义
- 1.3 策略的核函数
- 1.4 策略的类型
-
- 1.4.1 Softmax Policy
- 1.4.2 高斯分布
- 2. 正题:策略梯度RL
-
- 2.1 问题表征
- 2.2 MC梯度的方法
- 3. 改善策略梯度
-
- 3.1 考虑时序因果关系
- 3.2 采用Baseline
- 3.3 采用critic
- 3.4 采用Advantage function
- 3.5 TD Actor-Critic
- 4. 策略梯度高级算法
-
- Natural policy gradient(KL-divergence)
- importance sampling(IS)
- TRPO=IS+KL-divergence
- ACKTR
- PPO=simple TRPO
-
- PPO with Adaptive KL Penalty
- PPO with clipping
Policy-based RL
前言
此笔记根据周老师的强化学习课程总结而成
周老师的《强化学习纲要》
https://github.com/zhoubolei/introRL
∇ θ J ( θ ) = ∇ θ E π θ [ R ] \nabla_{\theta} J(\theta)=\nabla_{\theta} \mathbb{E}_{\pi_{\theta}}[R] ∇θJ(θ)=∇θEπθ[R]
1. 预备知识
1.1 策略类型
确定性策略和随机策略
1.2 策略优化的目标函数
1.2.1 可结束的环境的目标函数
用开始的第一个状态的价值来衡量策略的质量
J 1 ( θ ) = V π θ ( s 1 ) = E π θ [ v 1 ] J_{1}(\theta)=V^{\pi_{\theta}}\left(s_{1}\right)=\mathbb{E}_{\pi_{\theta}}\left[v_{1}\right] J1(θ)=Vπθ(s1)=Eπθ[v1]
1.2.3 连续动作环境的目标函数
取平均价值函数V
J a v V ( θ ) = ∑ s d π θ ( s ) V π θ ( s ) J_{a v V}(\theta)=\sum_{s} d^{\pi_{\theta}}(s) V^{\pi_{\theta}}(s) JavV(θ)=∑sdπθ(s)Vπθ(s)
取每一步的平均回报R
J a v R ( θ ) = ∑ s d π θ ( s ) ∑ a π θ ( s , a ) R ( s , a ) J_{a v R}(\theta)=\sum_{s} d^{\pi_{\theta}}(s) \sum_{a} \pi_{\theta}(s, a) R(s, a) JavR(θ)=∑sdπθ(s)∑aπθ(s,a)R(s,a)
where d π θ d^{\pi} \theta dπθ is stationary distribution of Markov chain for π θ \pi_{\theta} πθ
1.2.4 实际的目标函数的定义
利用采样的思想
J ( θ ) = E τ ∼ π θ [ ∑ t R ( s t τ , a t τ ) ] ≈ 1 m ∑ m ∑ t R ( s t m , a t m ) \begin{aligned} J(\theta) &=\mathbb{E}_{\tau \sim \pi_{\theta}}\left[\sum_{t} R\left(s_{t}^{\tau}, a_{t}^{\tau}\right)\right] \\ & \approx \frac{1}{m} \sum_{m} \sum_{t} R\left(s_{t}^{m}, a_{t}^{m}\right) \end{aligned} J(θ)=Eτ∼πθ[t∑R(stτ,atτ)]≈m1m∑t∑R(stm,atm)
策略优化的目标:
θ ∗ = arg max θ E τ ∼ π θ [ ∑ t R ( s t τ , a t τ ) ] \theta^{*}=\underset{\theta}{\arg \max }\mathbb{E}_{\tau \sim \pi_{\theta}}\left[\sum_{t} R\left(s_{t}^{\tau}, a_{t}^{\tau}\right)\right] θ∗=θargmaxEτ∼πθ[∑tR(stτ,atτ)]
1.3 策略的核函数
假设策略可微则
∇ θ π θ ( s , a ) = π θ ( s , a ) ∇ θ π θ ( s , a ) π θ ( s , a ) = π θ ( s , a ) ∇ θ log π θ ( s , a ) \begin{aligned} \nabla_{\theta} \pi_{\theta}(s, a) &=\pi_{\theta}(s, a) \frac{\nabla_{\theta} \pi_{\theta}(s, a)}{\pi_{\theta}(s, a)} \\ &=\pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a) \end{aligned} ∇θπθ(s,a)=πθ(s,a)πθ(s,a)∇θπθ(s,a)=πθ(s,a)∇θlogπθ(s,a)
其中策略的核函数: ∇ θ log π θ ( s , a ) \nabla_{\theta} \log \pi_{\theta}(s, a) ∇θlogπθ(s,a)
1.4 策略的类型
1.4.1 Softmax Policy
π θ ( s , a ) = exp ϕ ( s , a ) T θ ∑ a ′ exp ϕ ( s , a ′ ) T θ \pi_{\theta}(s, a)=\frac{\exp ^{\phi(s, a)^{T} \theta}}{\sum_{a^{\prime}} \exp ^{\phi\left(s, a^{\prime}\right)^{T} \theta}} πθ(s,a)=∑a′expϕ(s,a′)Tθexpϕ(s,a)Tθ
核函数: ∇ θ log π θ ( s , a ) = ϕ ( s , a ) − E π θ [ ϕ ( s , . ) ] \nabla_{\theta} \log \pi_{\theta}(s, a)=\phi(s, a)-\mathbb{E}_{\pi_{\theta}}[\phi(s, .)] ∇θlogπθ(s,a)=ϕ(s,a)−Eπθ[ϕ(s,.)]
其中 ϕ ( s , a ) \phi(s, a) ϕ(s,a)是状态-动作对的特征,动作的权重用特征的线性组合表示 ϕ ( s , a ) T θ \phi(s, a)^{T} \theta ϕ(s,a)Tθ
1.4.2 高斯分布
常用于连续动作的环境
π θ ( s , a ) = 1 σ 2 π e − 1 2 ( a − ϕ ( s ) T θ σ ) 2 \pi_{\theta}(s, a)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{a-\phi(s)^{T} \theta}{\sigma}\right)^{2}} πθ(s,a)=σ2π1e−21(σa−ϕ(s)Tθ)2
核函数: ∇ θ log π θ ( s , a ) = ( a − μ ( s ) ) ϕ ( s ) σ 2 \nabla_{\theta} \log \pi_{\theta}(s, a)=\frac{(a-\mu(s)) \phi(s)}{\sigma^{2}} ∇θlogπθ(s,a)=σ2(a−μ(s))ϕ(s)
其中 ϕ ( s ) \phi(s) ϕ(s)是状态的特征, 均值是状态特征的组合 μ ( s ) = ϕ ( s ) T θ \mu(s)=\phi(s)^{T} \theta μ(s)=ϕ(s)Tθ,方差可以是固定的也可以是参数化的
2. 正题:策略梯度RL
2.1 问题表征
利用1.2.4中的思想,即用采样的方法来表征目标函数 J ( θ ) = E π θ [ ∑ t = 0 T − 1 R ( s t , a t ) ] = ∑ τ P ( τ ; θ ) R ( τ ) J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\sum_{t=0}^{T-1} R\left(s_{t}, a_{t}\right)\right]=\sum_{\tau} P(\tau ; \theta) R(\tau) J(θ)=Eπθ[∑t=0T−1R(st,at)]=∑τP(τ;θ)R(τ)
τ = ( s 0 , a 0 , r 1 , … s T − 1 , a T − 1 , r T , s T ) ∼ ( π θ , P ( s t + 1 ∣ s t , a t ) ) \tau=\left(s_{0}, a_{0}, r_{1}, \ldots s_{T-1}, a_{T-1}, r_{T}, s_{T}\right) \sim\left(\pi_{\theta}, P\left(s_{t+1} \mid s_{t}, a_{t}\right)\right) τ=(s0,a0,r1,…sT−1,aT−1,rT,sT)∼(πθ,P(st+1∣st,at))用 π θ \pi_\theta πθ采样一个episode的轨迹。
P ( τ ; θ ) = μ ( s 0 ) ∏ t = 0 T − 1 π θ ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) P(\tau ; \theta)=\mu\left(s_{0}\right) \prod_{t=0}^{T-1} \pi_{\theta}\left(a_{t} \mid s_{t}\right) p\left(s_{t+1} \mid s_{t}, a_{t}\right) P(τ;θ)=μ(s0)∏t=0T−1πθ(at∣st)p(st+1∣st,at)一条采样轨迹的概率
R ( τ ) = ∑ t = 0 T − 1 R ( s t , a t ) R(\tau)=\sum_{t=0}^{T-1} R\left(s_{t}, a_{t}\right) R(τ)=∑t=0T−1R(st,at)一条轨迹上所有奖励的和
则我们的目标就是求
θ ∗ = arg max θ J ( θ ) = arg max θ ∑ τ P ( τ ; θ ) R ( τ ) \theta^{*}=\underset{\theta}{\arg \max } J(\theta)=\underset{\theta}{\arg \max } \sum_{\tau} P(\tau ; \theta) R(\tau) θ∗=θargmaxJ(θ)=θargmax∑τP(τ;θ)R(τ)
2.2 MC梯度的方法
将梯度进行类似1.3中的处理
∇ θ J ( θ ) = ∑ τ P ( τ ; θ ) R ( τ ) ∇ θ log P ( τ ; θ ) = E π θ ( R ( τ ) ∇ θ log P ( τ ; θ ) ) = E π θ [ ( ∑ t = 0 T − 1 r t ) ( ∑ t = 0 T − 1 ∇ θ log π θ ( a t ∣ s t ) ) ] \nabla_{\theta} J(\theta)=\sum_{\tau} P(\tau ; \theta) R(\tau) \nabla_{\theta} \log P(\tau ; \theta)=\mathbb{E}_{\pi_{\theta}}(R(\tau) \nabla_{\theta} \log P(\tau; \theta))=\mathbb{E}_{\pi_{\theta}}\left[\left(\sum_{t=0}^{T-1} r_{t}\right)\left(\sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right)\right] ∇θJ(θ)=∑τP(τ;θ)R(τ)∇θlogP(τ;θ)=Eπθ(R(τ)∇θlogP(τ;θ))=Eπθ[(∑t=0T−1rt)(∑t=0T−1∇θlogπθ(at∣st))]
则在实际中用采样的方法对其进行近似
∇ θ J ( θ ) ≈ 1 m ∑ i = 1 m R ( τ i ) ∇ θ log P ( τ i ; θ ) \nabla_{\theta} J(\theta) \approx \frac{1}{m} \sum_{i=1}^{m} R\left(\tau_{i}\right) \nabla_{\theta} \log P\left(\tau_{i} ; \theta\right) ∇θJ(θ)≈m1∑i=1mR(τi)∇θlogP(τi;θ)
对 ∇ θ log P ( τ ; θ ) \nabla_{\theta} \log P(\tau ; \theta) ∇θlogP(τ;θ)进行分解, ∇ θ log P ( τ ; θ ) = ∑ t = 0 T − 1 ∇ θ log π θ ( a t ∣ s t ) \nabla_{\theta} \log P(\tau ; \theta)=\sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) ∇θlogP(τ;θ)=∑t=0T−1∇θlogπθ(at∣st)
则目标函数的梯度变成:
∇ θ J ( θ ) ≈ 1 m ∑ i = 1 m R ( τ i ) ∑ t = 0 T − 1 ∇ θ log π θ ( a t i ∣ s t i ) \nabla_{\theta} J(\theta) \approx \frac{1}{m} \sum_{i=1}^{m} R\left(\tau_{i}\right) \sum_{t=0}^{T-1} \nabla_{\theta} \log\pi_\theta(a_{t}^{i}|s_{t}^{i}) ∇θJ(θ)≈m1∑i=1mR(τi)∑t=0T−1∇θlogπθ(ati∣sti)
由上式可以看到,目标函数的梯度的计算用不到环境模型 P ( s t + 1 ∣ s t , a t ) P\left(s_{t+1} \mid s_{t}, a_{t}\right) P(st+1∣st,at)
3. 改善策略梯度
基于采样的策略梯度是无偏有噪声的,下面就是为了消除噪声而进行的操作。
3.1 考虑时序因果关系
参考2.1 中的策略梯度函数,此策略梯度函数表示t时刻采样策略会影响t之前的回报r,其中的因果性就不合理,会引起较大的方差 ∇ θ J ( θ ) = E π θ [ ( ∑ t = 0 T − 1 r t ) ( ∑ t = 0 T − 1 ∇ θ log π θ ( a t ∣ s t ) ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\left(\sum_{t=0}^{T-1} r_{t}\right)\left(\sum_{t=0}^{T-1} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right)\right] ∇θJ(θ)=Eπθ[(∑t=0T−1rt)(∑t=0T−1∇θlogπθ(at∣st))]
现在为了去除因果性,考虑另一种表达方式
首先对于单个reward来说策略梯度为
∇ θ E π θ [ r t ′ ] = E π θ [ r t ′ ∑ t = 0 t ′ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} \mathbb{E}_{\pi_{\theta}}\left[r_{t^{\prime}}\right]=\mathbb{E}_{\pi_{\theta}}\left[r_{t^{\prime}} \sum_{t=0}^{t^{\prime}} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θEπθ[rt′]=Eπθ[rt′∑t=0t′∇θlogπθ(at∣st)]
然后summing整个reward ∇ θ J ( θ ) = ∇ θ E π θ [ R ] = ∇ θ E π θ [ ∑ t ′ = 0 T − 1 r t ′ ] = E τ [ ∑ t ′ = 0 T − 1 r t ′ ∑ t = 0 t ′ ∇ θ log π θ ( a t ∣ s t ) ] = E τ [ ∑ t = 0 T − 1 G t ⋅ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} J(\theta)=\nabla_{\theta} \mathbb{E}_{\pi_{\theta}}[R]=\nabla_{\theta} \mathbb{E}_{\pi_{\theta}}[\sum_{t^{\prime}=0}^{T-1}r_{t^{\prime}}]=\mathbb{E}_{\tau}\left[\sum_{t^{\prime}=0}^{T-1} r_{t^{\prime}} \sum_{t=0}^{t^{\prime}} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right]=\mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1} G_{t} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θJ(θ)=∇θEπθ[R]=∇θEπθ[∑t′=0T−1rt′]=Eτ[∑t′=0T−1rt′∑t=0t′∇θlogπθ(at∣st)]=Eτ[∑t=0T−1Gt⋅∇θlogπθ(at∣st)]
最后得到 ∇ θ J ( θ ) = E τ [ ∑ t = 0 T − 1 G t ⋅ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1} G_{t} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θJ(θ)=Eτ[∑t=0T−1Gt⋅∇θlogπθ(at∣st)]
根据最后得到的式子,采用MC采样的方法得到策略梯度的估计值
∇ θ J ( θ ) ≈ 1 m ∑ i = 1 m ∑ t = 0 T − 1 G t ( i ) ⋅ ∇ θ log π θ ( a t i ∣ s t i ) \nabla_{\theta} J(\theta)\approx \frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{T-1} G_{t}^{(i)} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t}^{i} \mid s_{t}^{i}\right) ∇θJ(θ)≈m1∑i=1m∑t=0T−1Gt(i)⋅∇θlogπθ(ati∣sti)
REINFORCE算法就是根据这一原理来进行设计的
3.2 采用Baseline
考虑3.1中得到的策略梯度函数,虽然去除了因果性,但是Gt也是采样出来的,它依然会有好,有坏,方差就会比较大。
∇ θ J ( θ ) = E τ [ ∑ t = 0 T − 1 G t ⋅ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1} G_{t} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θJ(θ)=Eτ[∑t=0T−1Gt⋅∇θlogπθ(at∣st)]
为了消除这个采样引起的方差,我们加入一个baseline,可以证明下面这个策略梯度和上面3.1中策略梯度是完全相同的,也是一个无偏估计,但是方差较小:
∇ θ J ( θ ) = E τ [ ∑ t = 0 T − 1 ( G t − b ( s t ) ) ⋅ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1}\left(G_{t}-b\left(s_{t}\right)\right) \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θJ(θ)=Eτ[∑t=0T−1(Gt−b(st))⋅∇θlogπθ(at∣st)]
其中advantage estimate= ( G t − b ( s t ) ) \left(G_{t}-b\left(s_{t}\right)\right) (Gt−b(st))
其中baseline可以用回报的期望表示 b ( s t ) = E [ r t + r t + 1 + … + r T − 1 ] b\left(s_{t}\right)=\mathbb{E}\left[r_{t}+r_{t+1}+\ldots+r_{T-1}\right] b(st)=E[rt+rt+1+…+rT−1]也可以用带参数的函数: b w ( s t ) b_{\mathrm{w}}\left(s_{t}\right) bw(st)
Vanilla Policy Gradient Algorithm with Baseline
3.3 采用critic
考虑3.1中得到的策略梯度函数,虽然去除了因果性,但是Gt也是采样出来的,它依然会有好,有坏,方差就会比较大。这个方差的来源是因为Gt是Q(at|st)的无偏有噪声估计
q π ( s , a ) ≐ E π [ G t ∣ S t = s , A t = a ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s , A t = a ] q_{\pi}(s, a) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s, A_{t}=a\right] qπ(s,a)≐Eπ[Gt∣St=s,At=a]=Eπ[∑k=0∞γkRt+k+1∣St=s,At=a]
可以看到对Gt取期望等于q,说明无偏差,但是毕竟是采样出来的所以noise比较大
∇ θ J ( θ ) = E τ [ ∑ t = 0 T − 1 G t ⋅ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\tau}\left[\sum_{t=0}^{T-1} G_{t} \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θJ(θ)=Eτ[∑t=0T−1Gt⋅∇θlogπθ(at∣st)]
为了消除这个采样引起的方差,我们直接用一个参数化的Q来代替Gt,后续不断地对其进行优化改进:
∇ θ J ( θ ) = E π θ [ ∑ t = 0 T − 1 Q w ( s t , a t ) ⋅ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\sum_{t=0}^{T-1} Q_{w}\left(s_{t}, a_{t}\right) \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θJ(θ)=Eπθ[∑t=0T−1Qw(st,at)⋅∇θlogπθ(at∣st)]
其中 Q w ( s , a ) ≈ Q π θ ( s , a ) Q_{\mathbf{w}}(s, a) \approx Q^{\pi_{\theta}}(s, a) Qw(s,a)≈Qπθ(s,a),被称为critic
最后观察上面这个等式 ∇ θ J ( θ ) = E π θ [ ∑ t = 0 T − 1 Q w ( s t , a t ) ⋅ ∇ θ log π θ ( a t ∣ s t ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\sum_{t=0}^{T-1} Q_{w}\left(s_{t}, a_{t}\right) \cdot \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right] ∇θJ(θ)=Eπθ[∑t=0T−1Qw(st,at)⋅∇θlogπθ(at∣st)]
其中 π θ ( a t ∣ s t ) \pi_{\theta}\left(a_{t} \mid s_{t}\right) πθ(at∣st)是Actor, Q w ( s t , a t ) Q_{\mathrm{w}}\left(s_{t}, a_{t}\right) Qw(st,at)是Critic。这个算法也叫做Actor-Critic Policy Gradient
一个简单的QAC算法
使用一个线性逼近函数来近似cirtic: Q w ( s , a ) = ψ ( s , a ) T w Q_{\mathbf{w}}(s, a)=\psi(s, a)^{T} \mathbf{w} Qw(s,a)=ψ(s,a)Tw
通过TD(0)的方式来更新w,用策略梯度的方法来更新 θ \theta θ(在lecture4有讲)

采用神经网络的方式更新
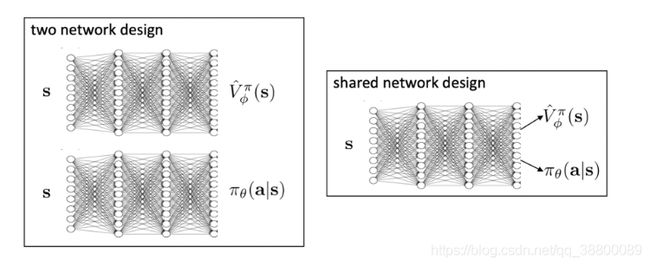
3.4 采用Advantage function
对于3.3中的Q依然存在方差,接下来继续减小方差,因为V是Q的期望值,所以我们用Q-V来作为advantage function:
$A^{\pi, \gamma}(s, a)=Q^{\pi, \gamma}(s, a)-V^{\pi, \gamma}(s) $
V π , γ ( s ) = E π [ r 1 + γ r 2 + … ∣ s 1 = s ] = E a ∼ π [ Q π , γ ( s , a ) ] \begin{aligned} V^{\pi, \gamma}(s) &=\mathbb{E}_{\pi}\left[r_{1}+\gamma r_{2}+\ldots \mid s_{1}=s\right] \\ &=\mathbb{E}_{a \sim \pi}\left[Q^{\pi, \gamma}(s, a)\right] \end{aligned} Vπ,γ(s)=Eπ[r1+γr2+…∣s1=s]=Ea∼π[Qπ,γ(s,a)]
Q π , γ ( s , a ) = E π [ r 1 + γ r 2 + … ∣ s 1 = s , a 1 = a ] Q^{\pi, \gamma}(s, a)=\mathbb{E}_{\pi}\left[r_{1}+\gamma r_{2}+\ldots \mid s_{1}=s, a_{1}=a\right] Qπ,γ(s,a)=Eπ[r1+γr2+…∣s1=s,a1=a]
从而策略梯度变成:
∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) A π , γ ( s , a ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) A^{\pi, \gamma}(s, a)\right] ∇θJ(θ)=Eπθ[∇θlogπθ(s,a)Aπ,γ(s,a)]
V v ( s ) ≈ V π ( s ) Q w ( s , a ) ≈ Q π ( s , a ) \begin{aligned} V_{\mathbf{v}}(s) & \approx V^{\pi}(s) \\ Q_{\mathbf{w}}(s, a) & \approx Q^{\pi}(s, a) \end{aligned} Vv(s)Qw(s,a)≈Vπ(s)≈Qπ(s,a)
V和Q参数的更新可以用TDlearning 或者 MC的方法
3.5 TD Actor-Critic
对于3.4中的策略梯度需要估计Q和V两个函数的参数,计算量比较大
∇ θ J ( θ ) = E π θ [ ∇ θ log π θ ( s , a ) A π , γ ( s , a ) ] \nabla_{\theta} J(\theta)=\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(s, a) A^{\pi, \gamma}(s, a)\right] ∇θJ(θ)=Eπθ[∇θlogπθ(s,a)Aπ,γ(s,a)]
A π , γ ( s , a ) = Q π , γ ( s , a ) − V π , γ ( s ) A^{\pi, \gamma}(s, a)=Q^{\pi, \gamma}(s, a)-V^{\pi, \gamma}(s) Aπ,γ(s,a)=Qπ,γ(s,a)−Vπ,γ(s)
现在通过一个变换,可以用只含有V
E π θ [ δ π θ ∣ s , a ] = E π θ [ r + γ V π θ ( s ′ ) ∣ s , a ] − V π θ ( s ) = Q π θ ( s , a ) − V π θ ( s ) = A π θ ( s , a ) δ π θ = r ( s , a ) + γ V π θ ( s ′ ) − V π θ ( s ) \begin{aligned} \mathbb{E}_{\pi_{\theta}}\left[\delta^{\pi_{\theta}} \mid s, a\right] &=\mathbb{E}_{\pi_{\theta}}\left[r+\gamma V^{\pi_{\theta}}\left(s^{\prime}\right) \mid s, a\right]-V^{\pi_{\theta}}(s) \\ &=Q^{\pi_{\theta}}(s, a)-V^{\pi_{\theta}}(s) \\ &=A^{\pi_{\theta}}(s, a) \\ \delta^{\pi_{\theta}}=& r(s, a)+\gamma V^{\pi_{\theta}}\left(s^{\prime}\right)-V^{\pi_{\theta}}(s) \end{aligned} Eπθ[δπθ∣s,a]δπθ==Eπθ[r+γVπθ(s′)∣s,a]−Vπθ(s)=Qπθ(s,a)−Vπθ(s)=Aπθ(s,a)r(s,a)+γVπθ(s′)−Vπθ(s)
可以采用MC和TD的方式来对V进行估计

总结:策略梯度的各种形式如下

4. 策略梯度高级算法
Policy Gradient → \rightarrow → Natural policy gradient / T R P O → A C K T R → P P O / \mathrm{TRPO} \rightarrow \mathrm{ACKTR} \rightarrow \mathrm{PPO} /TRPO→ACKTR→PPO
策略梯度的问题
1.采样比较少,效率比较低
2.训练用的数据间的相关度较高,训练过程可能会变得越来越糟,训练过程不稳定(比如采样到比较坏的数据,得到一个比较坏的策略。。。)
解决第一个问题:使用off-policy的方法,Importance sampling(TRPO)
解决第二个问题:增加Trust region(TRPO)和 Natural policy gradient
Natural policy gradient(KL-divergence)
这个方法是解决训练问题不稳定的情况。
基本的策略梯度方法是一个这样的优化问题 Δ θ ∗ = arg max J ( θ + Δ θ ) \Delta\theta^{*}=\arg \max J(\theta+\Delta\theta) Δθ∗=argmaxJ(θ+Δθ),在基本的策略梯度中 Δ θ ∗ = ∇ θ J ( θ ) \Delta\theta^{*}=\nabla_{\theta} J(\theta) Δθ∗=∇θJ(θ)。但是这样更新策略的参数有个问题,就是 θ \theta θ参数的变化对于策略的影响是未知的,可能会把一个比较不错的old策略带跑偏,容易产生震荡,也就是问题2。
解决问题2的方法,用KL-divergence对odl policy和new policy之间的差别进行约束
Δ θ ∗ = arg max J ( θ + Δ θ ) \Delta\theta^{*}=\arg \max J(\theta+\Delta\theta) Δθ∗=argmaxJ(θ+Δθ), s.t. K L ( π θ ∥ π θ + d ) = c K L\left(\pi_{\theta} \| \pi_{\theta+d}\right)=c KL(πθ∥πθ+d)=c
对其进行Lagrangian形式的处理,得到新的优化问题:
Δ θ ∗ = arg max Δ θ J ( θ + Δ θ ) − λ ( K L ( π θ ∥ π θ + Δ θ ) − c ) ≈ arg max Δ θ J ( θ ) + ∇ θ J ( θ ) T Δ θ − 1 2 λ Δ θ T F Δ θ + λ c \begin{aligned} \Delta\theta^{*} &=\underset{\Delta\theta}{\arg \max } J(\theta+\Delta\theta)-\lambda\left(K L\left(\pi_{\theta} \| \pi_{\theta+\Delta\theta}\right)-c\right) \\ & \approx \underset{\Delta\theta}{\arg \max } J(\theta)+\nabla_{\theta} J(\theta)^{T} \Delta\theta-\frac{1}{2} \lambda \Delta\theta^{T} F \Delta\theta+\lambda c \end{aligned} Δθ∗=ΔθargmaxJ(θ+Δθ)−λ(KL(πθ∥πθ+Δθ)−c)≈ΔθargmaxJ(θ)+∇θJ(θ)TΔθ−21λΔθTFΔθ+λc
对上面的优化问题进行梯度求导得
natural policy gradient: Δ θ ∗ = 1 λ F − 1 ∇ θ J ( θ ) \Delta\theta^{*}=\frac{1}{\lambda} F^{-1} \nabla_{\theta} J(\theta) Δθ∗=λ1F−1∇θJ(θ)
新的参数更新公式: θ t + 1 = θ t + α F − 1 ∇ θ J ( θ ) \theta_{t+1}=\theta_{t}+\alpha F^{-1} \nabla_{\theta} J(\theta) θt+1=θt+αF−1∇θJ(θ)
以前的参数更新公式: θ t + 1 = θ t + α ∇ θ J ( θ ) \theta_{t+1}=\theta_{t}+\alpha \nabla_{\theta} J(\theta) θt+1=θt+α∇θJ(θ)
对比这两个公式,这里新增加来一个F的逆,F是Fisher information matrix F = E π θ ( s , a ) [ ∇ log π θ ( s , a ) ∇ log π θ ( s , a ) T ] F=E_{\pi_{\theta}(s, a)}\left[\nabla \log \pi_{\theta}(s, a) \nabla \log \pi_{\theta}(s, a)^{T}\right] F=Eπθ(s,a)[∇logπθ(s,a)∇logπθ(s,a)T],F其实是策略的曲率,新的参数更新公式相较于以前的相当于把策略的曲率提除掉了。
importance sampling(IS)
为了改进第一个问题,我们采用得到的old policy对a进行采样,这样可以利用很多的样本。
J ( θ ) = E a ∼ π θ [ r ( s , a ) ] = E a ∼ π ^ [ π θ ( s , a ) π ^ ( s , a ) r ( s , a ) ] J(\theta)=\mathbb{E}_{a \sim \pi_{\theta}}[r(s, a)]=\mathbb{E}_{a \sim \hat{\pi}}\left[\frac{\pi_{\theta}(s, a)}{\hat{\pi}(s, a)} r(s, a)\right] J(θ)=Ea∼πθ[r(s,a)]=Ea∼π^[π^(s,a)πθ(s,a)r(s,a)]
从而优化问题变成
θ = arg max θ J θ old ( θ ) = arg max θ E t [ π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) R t ] \theta=\underset{\theta}{\arg \max } J_{\theta_{\text {old }}}(\theta)=\underset{\theta}{\arg \max } \mathbb{E}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} R_{t}\right] θ=θargmaxJθold (θ)=θargmaxEt[πθold (at∣st)πθ(at∣st)Rt]
TRPO=IS+KL-divergence
TRPO的优化问题
J θ old ( θ ) = E t [ π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) R t ] J_{\theta_{\text {old }}}(\theta)=\mathbb{E}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} R_{t}\right] Jθold (θ)=Et[πθold (at∣st)πθ(at∣st)Rt]
subject to K L ( π θ old ( . ∣ s t ) ∥ π θ ( . ∣ s t ) ) ≤ δ K L\left(\pi_{\theta_{\text {old }}}\left(. \mid s_{t}\right) \| \pi_{\theta}\left(. \mid s_{t}\right)\right) \leq \delta KL(πθold (.∣st)∥πθ(.∣st))≤δ
对上面两项泰勒展开后,经过推导得
J θ o l d ( θ ) ≈ g T ( θ − θ o l d ) K L ( θ o l d ∥ θ ) ≈ 1 2 ( θ − θ o l d ) F T ( θ − θ o l d ) \begin{aligned} J_{\theta_{old}}(\theta) & \approx g^{T}\left(\theta-\theta_{old}\right) \\ K L\left(\theta_{old} \| \theta\right) & \approx \frac{1}{2}\left(\theta-\theta_{old}\right)^{F} T\left(\theta-\theta_{old}\right) \end{aligned} Jθold(θ)KL(θold∥θ)≈gT(θ−θold)≈21(θ−θold)FT(θ−θold)
g = ∇ θ J θ o l d ( θ ) g=\nabla_{\theta} J_{\theta_{old}}(\theta) g=∇θJθold(θ) and T = ∇ θ 2 K L ( θ o l d ∣ ∣ θ ) T=\nabla_{\theta}^{2} K L\left(\theta_{old}|| \theta\right) T=∇θ2KL(θold∣∣θ)
然后优化形式就变成:
θ = arg max θ g T ( θ − θ o l d ) \theta=\underset{\theta}{\arg \max } g^{T}\left(\theta-\theta_{old}\right) θ=θargmaxgT(θ−θold) s.t. 1 2 ( θ − θ o l d ) T T ( θ − θ o l d ) ≤ δ \frac{1}{2}\left(\theta-\theta_{old}\right)^{T} T\left(\theta-\theta_{old}\right) \leq \delta 21(θ−θold)TT(θ−θold)≤δ
对上面的优化形式进行二次优化求解: θ = θ o l d + 2 δ g T H − 1 g T − 1 g \theta=\theta_{old}+\sqrt{\frac{2 \delta}{g^{T} H^{-1} g}} T^{-1} g θ=θold+gTH−1g2δT−1g
natural policy gradient: 2 δ g T T − 1 g T − 1 g \sqrt{\frac{2 \delta}{g^{T} T^{-1} g}} T^{-1} g gTT−1g2δT−1g
TRPO算法小结:
natural policy gradient:就是将KL-divergence考虑在内的梯度更新公式
ACKTR
用一个更简单的方法计算FIsher information matrix
PPO=simple TRPO
PPO是一种简化的TRPO实现形式,PPO的优化计算方式不用计算TRPO中的F二阶矩阵,比较容易实现计算也快很多,而且包括来TRPO中的IS和KL-divergence的特性。
对于TRPO中的loss function
maximize θ E t [ π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) A t ] _{\theta} \mathbb{E}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} A_{t}\right] θEt[πθold (at∣st)πθ(at∣st)At]
subject to E t [ K L [ π θ old ( . ∣ s t ) , π θ ( . ∣ s t ) ] ] ≤ δ \mathbb{E}_{t}\left[K L\left[\pi_{\theta_{\text {old }}}\left(. \mid s_{t}\right), \pi_{\theta}\left(. \mid s_{t}\right)\right]\right] \leq \delta Et[KL[πθold (.∣st),πθ(.∣st)]]≤δ
PPO不用解析的去求解,而是将其转化成拉格朗日的形式,也就是还是用一阶的SGD来对 θ \theta θ进行更新:
maximize θ E t [ π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) A t ] − β E t [ K L [ π θ old ( . ∣ s t ) , π θ ( . ∣ s t ) ] ] _{\theta} \mathbb{E}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} A_{t}\right]-\beta \mathbb{E}_{t}\left[K L\left[\pi_{\theta_{\text {old }}}\left(. \mid s_{t}\right), \pi_{\theta}\left(. \mid s_{t}\right)\right]\right] θEt[πθold (at∣st)πθ(at∣st)At]−βEt[KL[πθold (.∣st),πθ(.∣st)]]
PPO with Adaptive KL Penalty
动态的调整 β \beta β
PPO with clipping
再看原来的TRPO中的优化形式
maximize θ E t [ π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) A t ] _{\theta} \mathbb{E}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} A_{t}\right] θEt[πθold (at∣st)πθ(at∣st)At]
subject to E t [ K L [ π θ old ( . ∣ s t ) , π θ ( . ∣ s t ) ] ] ≤ δ \mathbb{E}_{t}\left[K L\left[\pi_{\theta_{\text {old }}}\left(. \mid s_{t}\right), \pi_{\theta}\left(. \mid s_{t}\right)\right]\right] \leq \delta Et[KL[πθold (.∣st),πθ(.∣st)]]≤δ
clip之后,形式变成:
maximize θ E t [ min ( π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) A t , clip ( π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) , 1 − ϵ , 1 + ϵ ) A t ) ] _{\theta} \mathbb{E}_{t}\left[\min \left(\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} {A}_{t}, \operatorname{clip}\left(\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)}, 1-\epsilon, 1+\epsilon\right) A_{t}\right)\right] θEt[min(πθold (at∣st)πθ(at∣st)At,clip(πθold (at∣st)πθ(at∣st),1−ϵ,1+ϵ)At)]
subject to E t [ K L [ π θ old ( . ∣ s t ) , π θ ( . ∣ s t ) ] ] ≤ δ \mathbb{E}_{t}\left[K L\left[\pi_{\theta_{\text {old }}}\left(. \mid s_{t}\right), \pi_{\theta}\left(. \mid s_{t}\right)\right]\right] \leq \delta Et[KL[πθold (.∣st),πθ(.∣st)]]≤δ
然后对上面的优化等式进行SGD求解
