拓端tecdat|python贝叶斯随机过程:马尔可夫链Markov-Chain,MC和Metropolis-Hastings,MH采样算法可视化
原文链接:http://tecdat.cn/?p=25428
原文出处:拓端数据部落公众号
介绍
本文,我们说明了贝叶斯学习和 计算统计一些结果。
from math import pi
from pylab import *
马尔可夫链的不变测度
考虑一个高斯 AR(1) 过程, ![]() , 其中
, 其中 ![]() 是标准高斯随机变量的独立同分布序列,独立于
是标准高斯随机变量的独立同分布序列,独立于 ![]() 。假使
。假使 ![]() .。然后,具有均值的高斯分布
.。然后,具有均值的高斯分布 ![]() 和方差
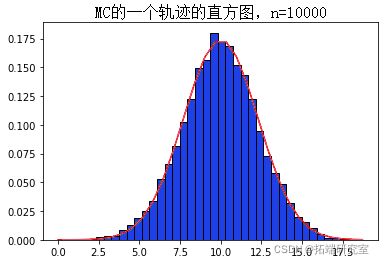
和方差 ![]() 是马尔可夫链的平稳分布。我们用马尔可夫链的单个轨迹所取值的直方图来检查这个属性。
是马尔可夫链的平稳分布。我们用马尔可夫链的单个轨迹所取值的直方图来检查这个属性。
f=lambda x,m,sq: np.exp(-(x-m)**2/(2*sq))/np.sqrt(2*pi*sq)
plt.hist第二个例子
我们在这里考虑一个马尔可夫链的例子,它的状态空间 ![]() 是开单位区间。如果链条在
是开单位区间。如果链条在 ![]() ,它等概率
,它等概率 ![]() 选择两个区间之一
选择两个区间之一 ![]() 或者
或者 ![]() ,然后移动到一个点,
,然后移动到一个点, ![]() 它均匀分布在选定的区间内。马尔可夫链的不变分布有 cdf,
它均匀分布在选定的区间内。马尔可夫链的不变分布有 cdf, ![]() 。 通过微分,我们可以得到相关的密度:
。 通过微分,我们可以得到相关的密度: ![]() 。对所有
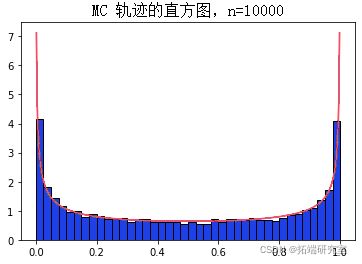
。对所有 ![]() , 我们现在用马尔可夫链取值的直方图检查这个属性。
, 我们现在用马尔可夫链取值的直方图检查这个属性。
x=arange(1,m)/m
for i in range(p-1):
[a,b]=rand(2)
plt.hist我们还可以说明直方图如何收敛到平稳分布的密度。这可以通过使用 matplotlib 中的“动画”模块的动态动画来完成。下面是python代码。
anm = animation.FuncAnimation以这个例子结束,这是一个动画。
data = []
for i in range(p-1):
[a,b]=npr.rand(2
if ((i+1)%100==0):
data.append
anim = animation.Func我们现在用一个例子来说明大数定律。如 ![]() 。 那么,我们期望
。 那么,我们期望 ![]() ,
,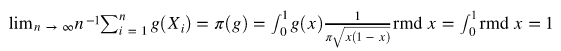
x=np.arange/(p)
for i in range(p-1):
[a,b]=npr.rand
m=np.cumsum(g(m))/np.arange(1,p+1)
plot对称随机游走 Metropolis Hasting 算法
我们现在考虑一个目标分布,它是两个高斯分布的混合,一个集中在 ![]() ,另一个集中在
,另一个集中在 ![]() 。
。
![]() 是中心标准正态分布的密度。
是中心标准正态分布的密度。
为了针对此分布,我们根据对称随机游走 Metropolis Hasting 算法进行采样。当链条处于状态时 ![]() ,我们提出一个候选
,我们提出一个候选 ![]() , 根据
, 根据 ![]() ,其中
,其中 ![]() 。然后我们接受
。然后我们接受 ![]() ,有概率
,有概率 ![]() , 其中
, 其中 ![]() . 否则,
. 否则, ![]() .
.
from IPython.display import HTML
rc('animation', html='jshtml')
ani独立Metropolis Hasting 算法
我们再次考虑一个目标分布,它是两个高斯分布的混合,一个集中在 ![]() ,另一个集中在
,另一个集中在 ![]() ,
,![]() ,其中
,其中 ![]() 是中心标准正态分布的密度。
是中心标准正态分布的密度。
为了针对这种分布,我们根据具有独立提议的 Metropolis Hasting 算法进行采样。当链条处于状态时 ![]() ,我们提出一个候选
,我们提出一个候选 ![]() ,根据
,根据 ![]() ,其中
,其中 ![]() 。然后我们接受
。然后我们接受 ![]() 有概率
有概率 ![]() , 其中
, 其中 ![]() 和
和 ![]() 是密度
是密度 ![]() .。否则,
.。否则, ![]() .。
.。
mc=npr.randn*np.one
data=[]
for i in range:
v=sig*npr+sft
alpha
if (npr.rand()最受欢迎的见解
1.matlab使用贝叶斯优化的深度学习
2.matlab贝叶斯隐马尔可夫hmm模型实现
3.R语言Gibbs抽样的贝叶斯简单线性回归仿真
4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归
5.R语言中的Stan概率编程MCMC采样的贝叶斯模型
6.Python用PyMC3实现贝叶斯线性回归模型
7.R语言使用贝叶斯 层次模型进行空间数据分析
8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
9.matlab贝叶斯隐马尔可夫hmm模型实现