算法系列--动态规划
一、动态规划
动态规划,dynamic programming。其实还是蛮头疼的,写这句话的时候也还没有完全搞懂,写这篇希望自己也可以彻底搞懂动态规划的套路。
动态规划,通常用来求解最优化问题,是通过组合子问题的解来求解原问题,与分治方法很相似。虽然都是将一个问题拆分为一堆更小的子问题,但动态规划更强调的是拆分出的子问题是否可以被重复调用。这样,对每一个子问题的计算结果保存起来,避免不必要的计算。
所以,其实动态规划的本质是穷举法,求解最优化问题,必然会将所有结果都结算出来,比较最值。但动态规划又不是简单的暴力计算穷举,只是不进行重复计算,从而得到最优解。
那什么场景会使用到动态规划呢?适合动态规划方法求解的问题应该具备两个要素:
- 重叠子问题
- 最优子结构
关于这两个要素的含义,下面进行解释一下
二、重叠子问题
如果递归算法反馈求解了相同的子问题,则称其具有重叠子问题性质。下面通过一个常见的算法问题来体验下重叠子问题的概念。
2.1 暴力递归解法
斐波那契数列大家应该都很熟悉,用代码表示其实就是递归:
public static int fibonacci(int n) {
if(n == 1 || n == 2){
return 1;
}
return fibonacci(n -1) + fibonacci(n-2);
}
简单的用图来表示下递归过程:
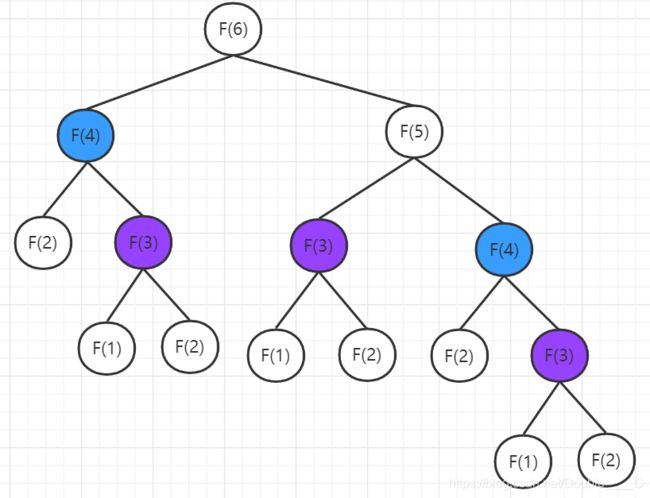
可以看到,在一个简单例子F(6)的计算过程中,已经出现了重复计算,F(4)计算了两次,F(3)计算了三次,而这个二叉树的算法复杂度则为O(2^n),显然当F(n)计算较大时,这个算法是很低效的,而且有可能会栈溢出。
从这个问题中我们看到了重叠子问题的性质,下面看一下动态规划思想中对重叠子问题的处理。
2.2 动态规划的思想
仍然使用递归,但这次在自顶向下的递归算法中增加了备忘机制。
public static int dyFib(int n) {
//备忘机制
List<Integer> tmp = new ArrayList<Integer>(Collections.nCopies(n+1, 0));
return dyFibTmp(tmp, n);
}
private static int dyFibTmp(List<Integer> tmp, int n) {
if(n == 1 || n == 2){
return 1;
}
if(tmp.get(n) != 0){
return tmp.get(n);
}
tmp.set(n,dyFibTmp(tmp,n-1) + dyFibTmp(tmp,n-2));
return tmp.get(n);
}
从上面的算法中,对自然但是低效的暴力递归算法做出来改良,就是通过备忘机制。我们通过维护一个list来纪录子问题的解,这样在随后每次遇到同一个子问题时,只是简单查询纪录的结果,并返回计算。
接在下来再看一种方法,使用自底向上的动态规划方法,这里就不引入备忘机制。
public static int dynamicFib(int n){
if(n == 1 || n == 2){
return 1;
}
int f1 = 1;
int f2 = 1;
//保存临时结果
int result = 0;
for (int i = 2; i < n; i++) {
result = f1 + f2;
f1 = f2;
f2 = result;
}
return result;
}
这个自底向上的动态规划算法,并不会使用递归,临时结果维护的开销也会更小一些。相对来说会比自定向下的备忘算法快。
三、最优子结构
如果一个问题的最优解包含其子问题的最优解,就可以说此问题具有最优子结构。当然,这也是判断当前问题是否适用于动态规划算法的重要因素之一。
动态规划中,对最优解的套路:
- 先求得子问题的最优解;
- 再求原问题的最优解
也就是说,问题的最优解就是在分解的子问题最优解再加上本次选择直接产生的解。
四、动态规划
下面看个有重叠子问题和最优子结构的动态规划算法问题:
零钱兑换:
给定不同面额的硬币 coins 和一个总金额
amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。你可以认为每种硬币的数量是无限的。
示例 1:输入:coins = [1, 2, 5], amount = 11 输出:3 解释:11 = 5 + 5 + 1 示例 2:
输入:coins = [2], amount = 3 输出:-1 示例 3:
输入:coins = [1], amount = 0 输出:0 示例 4:
输入:coins = [1], amount = 1 输出:1 示例 5:
输入:coins = [1], amount = 2 输出:2
提示:
1 <= coins.length <= 12 1 <= coins[i] <= 231 - 1 0 <= amount <= 104
下图对这个问题进行分析。以面值1,2,5硬币为例。从下面的图中,可以看出这个问题具有最优子结构和重叠子问题的特性。那么自然这个问题可以采用动态规划的方法来求解。

我们可以根据列出的解找出规律,列出此动态规划问题的状态转移方程,如下图所示:

所以根据状态转移方程,同时使用备忘方法来纪录已经计算过的子问题,同时对一些边界条件进行优化,下面就是此题使用动态规划问题的解法之一:
public static int coinChange(int[] coins, int amount){
int[] results = new int[amount+1];
Arrays.fill(results, amount+1);
results[0] = 0;
//计算从1元到amount元的最优个数
for (int i = 1; i <= amount; i++) {
//计算每个硬币的最后一步最优解
for (int j = 0; j < coins.length; j++) {
if(coins[j] <= i){
results[i] = Math.min(results[i],results[i-coins[j]]+1);
}
}
}
//防止出现付钱(即无法整除情况,预设最大值并判断)
return results[amount] > amount ? -1 : results[amount];
}