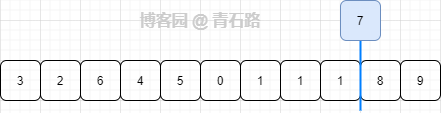再探快速排序 → 递进式演进，是否更容易理解？

开心一刻

　　爷爷有退休金，奶奶没有

　　可奶奶很要强

　　为了不让爷爷看不起，她找了份环卫的工作

　　结果要早起，她起不来

　　现在爷爷每天要早起扫大街

前情回顾

　　关于快排，楼主之前写过两篇关于它的文章

　　排序之快速排序 → 基本版实现，排序之快速排序 → 基本版优化

　　感觉讲的有点突兀，看过之后你们的表情是这样的

　　贴心的我实在是难以忍受你们那无辜的小眼神，决定让你们的表情变成这样

两区域划分

　　问题描述：给定一个整型数组 arr 和一个整数 target ，请把小于等于 target 的数放在数组的左边，大于 target 的数放在数组的右边

　　常规实现

　　如果不做任何限制，我相信大家很容易想到如下方法

　　准备一个新数组，然后遍历 arr ， arr 素逐个与 target 进行比较

　　小于等于 target 的元素从左往右放入到新数组中，大于 target 的元素从右往左放入到新数组中

　　当 arr 遍历完，新数组中的元素顺序即是：小于等于 target 的数在左边，大于 target 的数在右边

　　我们来看代码实现

　　假设 arr 是 [9,8,3,2,6,4,5,0,1,1,1] ， target 是 7，那么得到的结果是 [3,2,6,4,5,0,1,1,1,8,9] 

　　细心的小伙伴会大声道：你这不对，3 怎么在 2 的前面，6 的位置也不对，...

　　现在是区域划分，不是排序、不是排序、不是排序！

　　我们换个方式来看

　　现在清楚了吧

　　我们从两个维度来看看这个算法的优劣，时间复杂度 O(N) ，额外空间复杂度 O(N) 

　　时间复杂度已经没法优化，额外空间复杂度能不能优化了？

　　优化实现

　　常规实现中，用了一个新的数组，那有没有什么办法拿掉这个新数组后，仍然可以完成区域的划分了？

　　我们记录边界索引 lte ， lte 左边是小于等于区域， lte 至遍历索引 i 之间是大于区域，具体实现步骤如下

　　分两种情况进行处理

　　　　1、如果 arr[i] <= target ，则 arr[i] 和 lte 的前一个元素进行交换， lte 右移，i++

　　　　2、如果 arr[i] > target ， lte 不动，i++

　　我们看个具体案例就懂了

　　相当于小于等于区推着大于区往后走

　　再来看具体代码实现

　　此时，时间复杂度 O(N) ，只用到了一个额外变量 lte ，所以额外空间复杂度 O(1) 

荷兰国旗（三区域划分）

　　我们把问题进行一个升级：给定一个整型数组 arr ，和一个数  target ，请把小于 target 的数放在数组的左边，等于 target 的数放在数组的中间，大于 target 的数放在数组的右边

　　荷兰国旗是三种颜色

　　正好对应问题描述中的三个区域，所以也称这个问题为荷兰国旗问题

　　常规实现

　　可以在 两区域划分 的 常规实现 的基础上进行改造；我们直接看代码

　　很明显，时间复杂度 O(N) ，额外空间复杂度 O(N) 

　　时间复杂度已经没法优化了，我们需要优化额外空间复杂度

　　优化实现

　　如果要求额外空间复杂度 O(1)，时间复杂度 O(N)

　　类比 两区域划分 的 优化实现 ，我们分两个边界索引，左边界索引 lt 往左是小于区，右边界索引 gt 往右是大于区， lt 至遍历索引 i 之间是等于区域，i 至 gt 之间是待定（未比较）区域

　　分三种情况进行处理：

　　　　1、 arr[i] < target ， arr[i] 和 lt 后一个元素进行交换， lt 右移，i++

　　　　2、 arr[i] == target ，i++

　　　　3、 arr[i] > target ， arr[i] 和 gt 前一个元素进行交换， gt 左移，i 不动

　　我们来看个具体案例就理解了

　　是不是有点感觉了？

　　我们再来看看代码的实现

　　时间复杂度 O(N) ，仅用了有限几个变量，额外空间复杂度 O(1) 

快速排序

　　配角已经悉数登场，接下来有请主角登场

　　1.0 版本

　　基于 两区域划分 ，我们来实现快速排序

　　1、我们取最后一个元素作为 target ，将最后一个元素之前（不包括最后一个元素）所有元素进行一次 两区域划分 ，然后将大于区的第一个元素与 target 进行交换

　　2、此时 target 所在的位置是 lte + 1 ，然后对 left ~ lte 和 lte+2 ~ right 这两个区域分别做 两区域划分 

　　3、重复步骤1、2，最终实现排序

　　直接看代码

　　2.0 版本

　　类似 荷兰国旗问题 对 两区域划分 的优化，一次处理一批等于 target 的元素

　　处理步骤与 1.0 版本 类似，如下

　　1、取最后一个元素作为 target ，将最后一个元素之前的元素按 荷兰国旗问题 处理，然后将大于区域的第一个元素与 target 进行交换

　　2、此时， lt+1 ~ gt 范围的元素都等于 target ，不需要再处理；只需要对 left ~ lt 和 gt+1~ right 这两个区域分别做 荷兰国旗问题 处理

　　3、重复步骤1、2，最终实现排序

　　代码实现如下：

　　3.0 版本

　　不管是 1.0 版本 还是 2.0 版本 ，时间复杂度都是 O(N²)，比如对 [1,2,3,...,N-1,N] 进行排序

　　时间复杂度就是：O( N-1 + N-2 + ... + 2 + 1 )，常数项可以忽略，也就是 O(N²)

　　因为我们取 target 的时候，固定取的最右边元素，所以我们需要随机取 target 

　　我们可以从 left ~ right 中随机取一个元素作为 target ，然后以此 target 对 arr[left...right] 做 荷兰国旗问题 处理

　　代码实现如下：

　　partition 版本

　　其实就是 3.0 版本 的另外一种叫法

　　实现基本一致，如下

总结

　　演进过程

　　从 两区域划分 ->  荷兰国旗问题 -> 快速排序 

　　快排 1.0 -> 快排 2.0 -> 快排 3.0

　　递进式实现，便于大家理解快速排序

　　注意点

　　实现的过程中，一些边界值需要注意

　　边画图，边梳理，结合实际案例进行分析实现