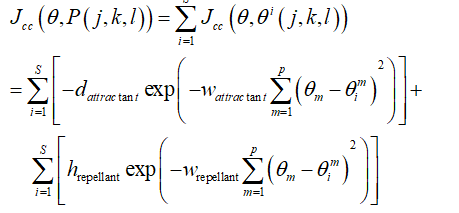基于matlab的捕食算法,【优化求解】基于matlab细菌觅食算法的函数优化分析【含Matlab源码 217期】...
一、简介
实际生活需求促进了最优化方法的发展。近半个多世纪以来,由于传统优化方法的不足,一些具有全局优化性能且通用性强的进化算法,因其高效的优化性能、无需问题精确描述信息等优点,受到各领域广泛的关注和应用。其中产生最早也最具代表性的进化算法是20世纪70年代源于达尔文自然选择学说和孟德尔遗传变异理论的遗传算法(Genetic Algorithm,GA)。而近年来,人们模拟自然界生物群体行为产生出一系列群体智能优化算法,如Dorigo等通过模拟蚂蚁的寻径行为于1991年提出了蚁群优化算法(Ant Colony Optimization,ACO);Eberhart和Kennedy通过模拟鸟群捕食行为于1995年提出了粒子群优化算法(Particle Swarm Optimization,PSO)。这些算法被广泛应用于工程领域并取得了显著的成果。随着群体智能优化算法的蓬勃发展,Passino于2002年提出了模拟人类大肠杆菌觅食行为的细菌觅食优化算法(Bacteria Foraging Optimization Algorithm,BFOA),为仿生进化算法家族增添了新成员。本章将着重向广大编程爱好者介绍最基本的细菌觅食算法,各编程科研人员可以基于本章算法加以改进并应用到实际案例中。
1 标准细菌觅食优化算法
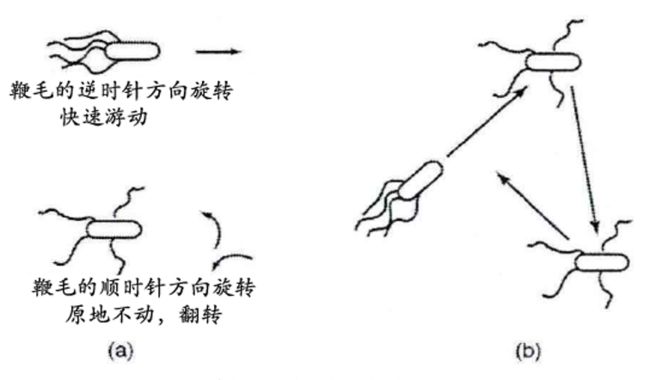
2 趋向性操作(Chemotaxis)
3 聚集性操作(Swarming)
4 复制性操作(Reproduction)
5 迁徙性操作(Elimination and Dispersal)
实际环境中的细菌所生活的局部区域可能会发生逐渐变化(如食物消耗殆尽)或者发生突如其来的变化(如温度突然升高等)。这样可能会导致生活在这个局部区域的细菌种群被迁徙到新的区域中去或者集体被外力杀死。在BFO算法中模拟这种现象称为迁徙性操作。
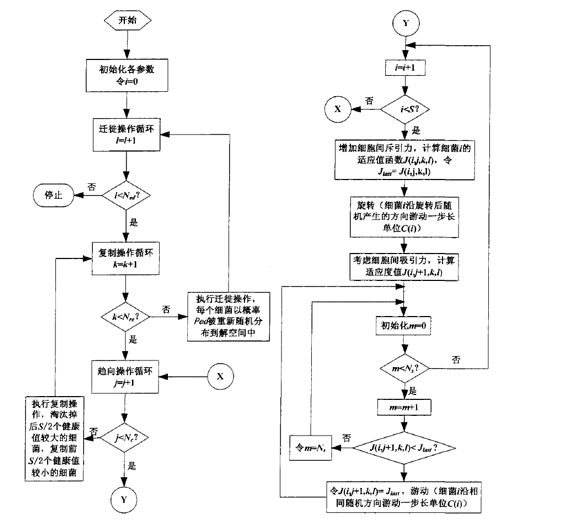
6 BFO算法流程
二、源代码
%%%%%%%%%%%%-----BF0算法-----%%%%%%%%%%%%%%%
clc; clear; close all
warning off
feature jit off % 加速代码执行
%-----初始化参数-----
bounds = [-5.12, 5.12;-5.12, 5.12]; % 函数变量范围
p = 2; % 搜索范围的维度
s = 26; % 细菌的个数
Nc = 50; % 趋化的次数
Ns = 4; % 趋化操作中单向运动的最大步数
C(:,1) = 0.001*ones(s,1); % 翻转选定方向后,单个细菌前进的步长
Nre = 4; % 复制操作步骤数
Ned = 2; % 驱散(迁移)操作数
Sr = s/2; % 每代复制(分裂)数
Ped = 0.25; % 细菌驱散(迁移)概率
d_attract = 0.05; % 吸引剂的数量
ommiga_attract = 0.05; % 吸引剂的释放速度
h_repellant = 0.05; % 排斥剂的数量
ommiga_repellant = 0.05; % 排斥剂的释放速度
for i = 1:s % 产生初始细菌个体的位置
P(1,i,1,1,1) = -5.12 + rand*10.24;
P(2,i,1,1,1) = -5.12 + rand*10.24;
end
%----细菌趋药性算法循环开始
%---- 驱散(迁移)操作开始
for l = 1:Ned
%-----复制操作开始
for k = 1:Nre
%-----趋化操作(翻转或游动)开始
for j = 1:Nc
%-----对每一个细菌分别进行以下操作
for i = 1:s
%-----计算函数J(i,j,k,l),表示第i个细菌在第l次驱散第k次
%--------复制第j次趋化时的适应度值
J(i,j,k,l) = fitness(P(:,i,j,k,l));
%-----修改函数,加上其它细菌对其的影响
Jcc = sum(-d_attract*exp(-ommiga_attract*((P(1,i,j,k,l)-...
P(1,1:26,j,k,l)).^2+(P(2,i,j,k,l)-P(2,1:26,j,k,l)).^2)))+...
sum(h_repellant*exp(-ommiga_repellant*((P(1,i,j,k,l)-...
P(1,1:26,j,k,l)).^2+(P(2,i,j,k,l)-P(2,1:26,j,k,l)).^2)));
J(i,j,k,l) = J(i,j,k,l) + Jcc;
%----保存细菌目前的适应度值,直到找到更好的适应度值取代之
Jlast = J(i,j,k,l);
%-----翻转,产生一个随机向量C(i),代表翻转后细菌的方向
Delta(:,i) = (2*round(rand(p,1))-1).*rand(p,1);
% PHI表示翻转后选择的一个随机方向上前进
PHI = Delta(:,i)/sqrt(Delta(:,i)'*Delta(:,i));
%-----移动,向着翻转后细菌的方向移动一个步长,并且改变细菌的位置
P(:,i,j+1,k,l) = P(:,i,j,k,l) + C(i,k)*PHI;
%-----计算细菌当前位置的适应度值
J(i,j+1,k,l) = fitness(P(:,i,j+1,k,l));
%-----游动-----
m = 0; % 给游动长度计数器赋初始值
while(m < Ns) % 未达到游动的最大长度,则循环
m = m + 1;
% 新位置的适应度值是否更好?如果更好,将新位置的适应度值
% 存储为细菌i目前最好的适应度值
if(J(i,j+1,k,l)
Jlast = J(i,j+1,k,l); % 保存更好的适应度值
% 在该随机方向上继续游动步长单位,修改细菌位置
P(:,i,j+1,k,l) = P(:,i,j+1,k,l) + C(i,k)*PHI;
% 重新计算新位置上的适应度值
J(i,j+1,k,l) = fitness(P(:,i,j+1,k,l));
else
% 否则,结束此次游动
m = Ns;
end
end
三、运行结果
四、备注
标签:217,求解,算法,源码,Matlab,优化,matlab
来源: https://blog.csdn.net/TIQCmatlab/article/details/113642565