第27期 Datawhale 组队学习 吃瓜教程——西瓜书+南瓜书第三章 / 周志华《机器学习》
说明: 本次学习是基于西瓜书,南瓜书,及部分网上参考资料(链接会放在最后)
线性模型目录
- 1. 基本定义
-
- 1.1 基本形式
- 2. 线性回归(回归问题)
-
-
-
- 扩展:离散信息如何转换为连续信息
-
- 2.1 单元线性回归
-
- 2.1.1 数学公式,求 ω {\omega } ω 与 b b b(均方误差/别名最小二乘法)
- 2.1.2 代码
-
- 数学原理版:
- 调库版(sklearn)
- 2.2 多元线性回归
-
- 2.2.1 数学公式,求 ω {\omega } ω 与 b b b
- 2.2.2 代码
-
- 数学原理版:
- 2.3 对数几率回归(说是回归,其实线性部分隐含地做了一个回归,最终目标还是以解决分类问题为主。)
-
- 2.3.1 广义线性模型
- 2.3.2 对数几率回归
-
- 2.3.2.1 数学公式
- 2.3.2.2 数学推导
-
- 3. 线性分类(分类型问题)
-
- 3.1 线性判别分析(LDA)
-
- 3.1.* 公式推导
- 3.2 多分类学习
-
- 3.2.1 OvO与 OvR
- 3.2.2 MvM
- 4. 类别不平衡问题
- 5. 参考文献
1. 基本定义
1.1 基本形式
f ( X ) = ω 1 x 1 + ω 2 x 2 + ω 3 x 3 + . . . + ω d x d + b { f(X)= \omega_1 x_1+ \omega_2 x_2+ \omega_3 x_3+...+ \omega_d x_d+b} f(X)=ω1x1+ω2x2+ω3x3+...+ωdxd+b
一般用向量形式写成
f ( X ) = ω T X + b \\ { f(X)= \omega^T X +b} f(X)=ωTX+b
其中 ω = ( ω 1 ; ω 2 ; ω 3 ; . . . ; ω d ) {\omega=(\omega_1;\omega_2;\omega_3;...;\omega_d)} ω=(ω1;ω2;ω3;...;ωd), ω \omega ω和b学得后,模型确定。
2. 线性回归(回归问题)
因为是回归问题所以得出的结果为离散值,对离散属性或非数字化属性,若存在序的关系(就是渐进性关系),我们可以赋予其数据以代替,即将其连续化转为连续值(例如:熟了,半熟,生的可以转化为{1.0,0.5,0},可转为向量 { (1,0,0),(0,1,0),(0,0,1) } )。
根本上还是求 f ( X ) = ω T X + b f(X)=\omega^T X +b f(X)=ωTX+b,使得 f ( x ) ≈ y i {f(x)\approx y_i } f(x)≈yi
扩展:离散信息如何转换为连续信息
- 如果数据是二元离散特征,则可以(白:0,黑:1)
- 如果数据是有序多元离散特征,则是(小:1,中:2,大:3)
- 如果数据是无序多元离散特征,则是(熟了,半熟,生的可转为向量 { (1,0,0),(0,1,0),(0,0,1) } )。
2.1 单元线性回归
2.1.1 数学公式,求 ω {\omega } ω 与 b b b(均方误差/别名最小二乘法)
关键在建立一个标准去求出 f ( x ) f(x) f(x)与 y i y_i yi之间的差别,此处使用均方误差,即
( ω ∗ , b ∗ ) = a r g m i n ∑ i = 1 n ( f ( x i ) − y i ) 2 \begin{array}{cc} \ {(\omega^*,b^*)=arg min\displaystyle \sum_{i=1}^{n}(f(x_i)-y_i)^2} \end{array} (ω∗,b∗)=argmini=1∑n(f(xi)−yi)2
即:
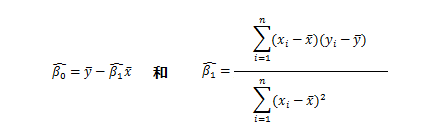

2.1.2 代码
数学原理版:
import numpy as np
import matplotlib.pyplot as plt
x1 = [1, 3, 5, 8, 11, 13, 16, 19] # 随机定义数1
y1 = [2, 6, 8, 10, 16, 18, 20, 25] # 随机定义数2
sum_x = 0
for i in range(len(x1)):
sum_x += x1[i]
sum_y = 0
for j in range(len(y1)):
sum_y += y1[j]
average_x = sum_x / len(x1)
average_y = sum_y / len(y1)
# y=ax+b
sum1 = 0
for i in range(len(x1)):
sum1 += y1[i] * x1[i]
sum1 -= sum_y * average_x
sum2 = 0
for i in range(len(x1)):
sum2 += x1[i] ** 2
sum3 = sum_x ** 2 / len(x1)
a = sum1 / (sum2 - sum3)
b = average_y - a * average_x
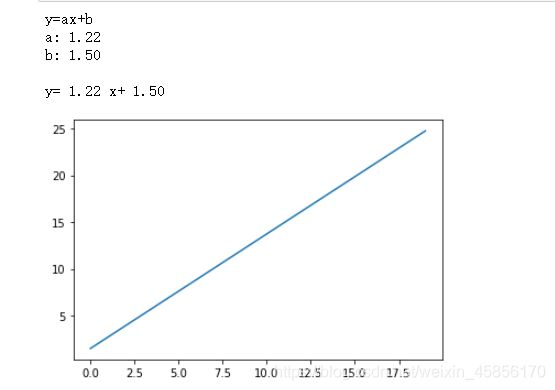
print("y=ax+b")
print("a:",'%.2f'%a,"\nb:",'%.2f'%b,"\n")
print("y=",'%.2f'%a,"x+",'%.2f'%b)
x = np.arange(0, 20)
y = a*x + b
plt.plot(x, y) # 建立坐标
plt.show()
调库版(sklearn)
参考文献:【机器学习】python实现线性回归 sklearn库
from sklearn import linear_model
from pylab import *#这一句话就引入了numpy、matplotlib等常用库,避免了多个import语句。
mpl.rcParams['font.sans-serif'] = ['SimHei']#python用来正常显示中文标签
X = np.array([[150, 200, 250, 300, 350, 400, 600]]).reshape(7, 1)
Y = np.array([[6450, 7450, 8450, 9450, 11450, 15450, 18450]]).reshape(7, 1)
# 建立线性回归模型
regr = linear_model.LinearRegression()
# 拟合
regr.fit(X, Y)
# 不难得到直线的斜率、截距
a, b = regr.coef_, regr.intercept_
# 给出预测面积,预测房子价格price
area = np.array([[238.5]]).reshape(-1, 1)
# 作图
# 1.真实数据的点
plt.scatter(X, Y, color='blue', label='原始数据点')
# 2.拟合的直线
plt.plot(X, regr.predict(X), color='red', linewidth=4, label='拟合线')
plt.xlabel("square_feet")
plt.ylabel("price")
plt.grid()
plt.legend()
plt.show()
2.2 多元线性回归
2.2.1 数学公式,求 ω {\omega } ω 与 b b b
公式:
f ( X i ) = ω T X i + b , 使 得 f ( x i ) ≈ y i \\ { f(X_i)= \omega^T X_i +b,使得f(x_i)\approx y_i} f(Xi)=ωTXi+b,使得f(xi)≈yi
与单元线性回归区别:计算方式的改变,由数值的运算,转变为了矩阵之间的关系(其实前面一个也可以这样搞,只是没写)
求法:
在 X T X X^TX XTX为满秩矩阵或正定矩阵时: ω ∗ = ( X T X ) − 1 X T y {\omega^*=(X^TX)^{-1}X^Ty } ω∗=(XTX)−1XTy
 数学证明:多元线性回归中的公式推导
数学证明:多元线性回归中的公式推导
2.2.2 代码
数学原理版:
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt
# 定义训练数据
x = np.array([[100, 4, 9.3], [50, 3, 4.8], [100, 4, 8.9],
[100, 2, 6.5], [50, 2, 4.2], [80, 2, 6.2],
[75, 3, 7.4], [65, 4, 6], [90, 3, 7.6], [90, 2, 6.1]])
print(x)
X = x[:, :-1]
Y = x[:, -1]
print(X, Y)
# 训练数据
regr = linear_model.LinearRegression()
regr.fit(X, Y)
print('coefficients(b1,b2...):', regr.coef_)
print('intercept(b0):', regr.intercept_)
# 预测
x_test = np.array([[102, 6], [100, 4]])
y_test = regr.predict(x_test)
print(y_test)
x = np.array([[1,1],[2,2],[3,3],[4,4]])
y = regr.predict(x)
plt.plot(x, y) # 建立坐标
plt.show()
2.3 对数几率回归(说是回归,其实线性部分隐含地做了一个回归,最终目标还是以解决分类问题为主。)
2.3.1 广义线性模型
如果想要模型得到预测值逼近y的衍生物,例如我们认为数据是在指数尺度变化,则可以得到 l n y = g − 1 ( ω T x + b ) {ln\ y=g^{-1}(\omega^Tx+b)} ln y=g−1(ωTx+b),如果将这个结论推导更大范围下,则可以得到,对与任意单调可微函数 g ( ⋅ ) g(\cdot) g(⋅),令
y = g − 1 ( ω T x + b ) y={g^{-1}(\omega^Tx+b)} y=g−1(ωTx+b)
其中 g ( ⋅ ) g(\cdot) g(⋅)被称为联系函数。
2.3.2 对数几率回归
2.3.2.1 数学公式
考虑到对数几率回归,本质上依然是为了解决二分类问题,而线性回归模型产生的预测值 y = g − 1 ( ω T x + b ) y={g^{-1}(\omega^Tx+b)} y=g−1(ωTx+b)是实值,即需要将实值y转化为0/1值,所以使用"单位阶跃函数"
y = { 0 , z < 0 0.5 , z = 0 1 , z > 0 {y=}\begin{cases} \ {0\ \ ,z<0} \\ {0.5,z=0} \\ {1 \ \ ,z>0} \end{cases} y=⎩⎪⎨⎪⎧ 0 ,z<00.5,z=01 ,z>0

(中间那个点不好看,看不太清)
因为阶跃函数不连续,所以我们使用替代品对数几率函数(sigmoid函数):
y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1
引申概念:几率:若y视x作为正例的可能性,则 y 1 − y \frac{y}{1-y} 1−yy,反应x作为正例的可能性,被称为几率。

2.3.2.2 数学推导
机器学习入门学习笔记:(2.3)对数几率回归推导
3. 线性分类(分类型问题)
3.1 线性判别分析(LDA)
说明:给定训练样本集,设法将样例投影到一条直线上,使得同类样例的投影点要尽可能相近,异类投影点尽可能远离。
公式: Y = ω T X {Y=\omega^TX} Y=ωTX
3.1.* 公式推导
线性判别分析LDA原理及推导过程(非常详细)
3.2 多分类学习
思路:将多分类问题转化为若干个二分类任务求解。
经典拆分策略:“一对一”(OvO),“一对其余”(OvR),“多对多"(MvM)
优秀文献:机器学习入门 9-8 OvR与OvO
3.2.1 OvO与 OvR
3.2.2 MvM
原理:每次将若干个类作为正类,若干个其他类作为反类
最常用技术:纠错输出码(ECOC)
ECOC工作过程:
- 编码:对若干个类做m次类别划分,每次将一部分类作为正类,一部分作为反类,形成一个二分类训练集,这样产生m个训练集,可训练出m个分类器
- 解码:m个分类器分别对测试样本进行预测,这些预测标记组成一个编码,将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为预测结果。
4. 类别不平衡问题
分类中常见的类别不平衡问题解决方法
5. 参考文献
- 机器学习入门 9-8 OvR与OvO
- ovo以及ovr的直观理解
- 分类中常见的类别不平衡问题解决方法
- 多元线性回归中的公式推导
- 机器学习入门学习笔记:(2.3)对数几率回归推导
- 线性判别分析LDA原理及推导过程(非常详细)