今天翻到一个以前回答的问题:从列表中随机抽取一定数量的数据。之前回答是使用 Fisher-Yates 洗牌算法来解决的,但是阅读了评论之后,又有了一些新想法。
先不说是什么算法,只说说随机抽取的思路。
随机抽取的算法演进
假设有 n 个数据保存在一个列表 source 中(在 JavaScript 中是数组),需要随机抽取 m (m <= n) 个数据出来,结果放在另一个列表 result 中。由于随机抽取是一个重复过程,可以使用一个 m 次的循环来完成,循环体中每次从 source 中选一个数出来(找到它,并把它从 source 中删除),依次放在 result 中。用 JavaScript 来描述就是
function randomSelect(source, m) {
const result = [];
for (let i = 0; i < m; i++) {
const rIndex = ~~(Math.random() * source.length);
result.push(source[rIndex]);
source.splice(rIndex, 1);
}
return result;
}在多数语言中,从列表中间删除一个数据,都会造成之后的数据重排,是个较低效率的操作。考虑到从一组数据中随机抽取一个是等概率事件,与数据所在的位置无关,我们可以把选出来的数据去掉之后,不减少列表长度,而是直接把列表最后一个数据挪过来。下一次随机取找位置的时候,不把最后一个元素考虑在内。这样改进之后的算法:
function randomSelect(source, m) {
const result = [];
for (let i = 0, n = source.length; i < m; i++, n--) {
// ^^^^^^^^^^^^^^^^^ ^^^
const rIndex = ~~(Math.random() * n);
result.push(source[rIndex]);
source[rIndex] = source[n - 1];
// ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
}
return result;
}注意到这里 n-- 和 n - 1 是可以合并的,合并后:
for (let i = 0, n = source.length; i < m; i++) {
...
source[rIndex] = source[--n];
}这时候,再次注意到,source 后面没用的空间,其实是和 result 空间一样大的,如果把这部分空间利用起来,就不再需要 result。
function randomSelect(source, m) {
for (let i = 0, n = source.length; i < m; i++) {
const rIndex = ~~(Math.random() * n);
--n;
// 交换选中位置的数据和当前最后一个位置的数据
[source[rIndex], source[n]] = [source[n], source[rIndex]];
}
// 把后面 m 个数据返回出来就是随机选中的
return source.slice(-m); // -m 和 source.length - m 等效
}如果保留原来的 result 及相关算法,会发现 result 和现在返回的数组元素正好是相反序排列的。但是不重要,因为我们的目的是随机选择,不管是否 revert,结果集都是随机的。
但是这么一来,假设 m = source.length,整个 source 中的数据都都被随机排列了 —— 这就是 Fisher-Yates 算法。当然,实际上只需要进行 source.length - 1 次处理就可以达到完全洗牌的效果。
Fisher-Yates 洗牌 (shuffle) 算法
Fisher-Yates 高效和等概率的洗牌算法。其核心思想是从 1 到 n 之间随机抽取出一个数和最后一个数 (n) 交换,然后从 1 到 n-1 之间随机出一个数和倒数第二个数 (n-1) 交换……,经过 n - 1 轮之后,原列表中的数据就被完全随机打乱了。
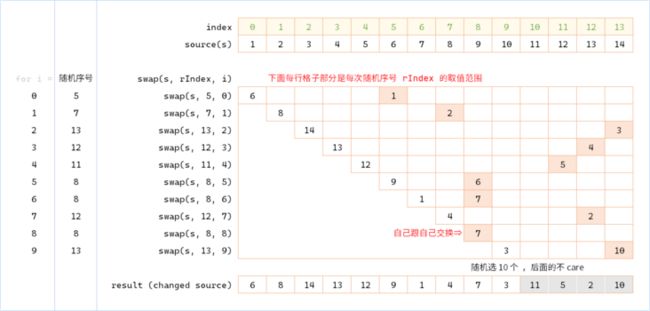
每次和“当前最后一个元素交换”会把处理结果后置。如果改为每次与当前位置(即 i 位置)元素交换,就可以把结果集前置。但要注意随机数的选择就不是 [0, n) (0 < n < source.length) 这个范围,而是 [i, source.length) 这个范围了:
function randomSelect(source, m) {
for (let i = 0, n = source.length; i < m; i++, n--) {
const rIndex = ~~(Math.random() * n) + i;
[source[rIndex], source[i]] = [source[i], source[rIndex]];
}
return source.slice(0, m);
}这个过程可以用一个图来帮助理解(随机选 10 个)
既然是洗牌算法,在数据量不大的情况下,可以使用现成的工作函数洗牌再从中取出来指定大小的连续数据就可以实现随机抽取的目的。比如使用 Loadsh 的 _.shuffle() 方法。
import _ from "lodash";
const m = 10;
const result = _.shuffle(data).slice(0, m);这里有两个问题
- 如果原数据量较大,或者原数据数量与要抽取的数据数量差异较大,会浪费很多算力
- 洗牌算法会修改原始数据集中的元素顺序
对于第一个问题,使用前面手工敲的 randomSelect() 就行了,第二个问题下面专门来讨论。
改进,不修改原数据集
要想不改变原数据,那就是不对数据源中的元素进行交换或移位。但是需要知道哪些数据已经被选过,应该怎么办呢?有如下几种方法
- 附加一个已选择元素序号集,如果某次算出来的
rIndex能在这个集合中找到,就重新选一次。
这是个办法,但随着可选序号和不可选序号的比例逐渐变小,重选的概率会大大增加,完全不能保证整个算法的效率。 - 同样按上述方法使用一个已选择序号集,但是发生碰撞的时候不重选,而是对序号进行累加取模。
这个方法比上一个要稳定一些,但仍然存在不太稳定的累加计算,而且可能会降低随机性。 - ……
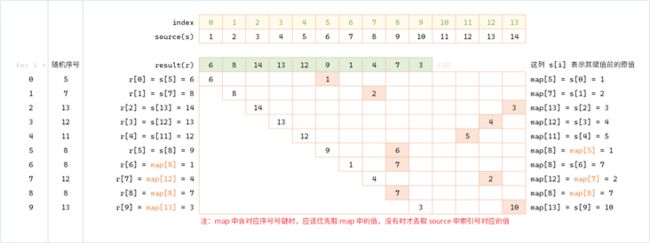
仔细想想,之前我们把最后一个未使用元素与 rIndex 所在元素进行交换的目的,就是为了让 rIndex 再次出现时能命中一个未取到的值 —— 假设这个值不是从原数据集中去取,而是从一个附加的数据集去取呢?
举例来说,rIndex = 5 的情况,第一次取 source[5] 得到 6,此时本应该把最后一个值赋过来,也就是 source[5] = source[13] = 14。我们把这个赋值过程改为 map[5] = source[13] = 14;下一次再命中 rIndex = 5 的时候,先去检查 map 中是否存在 map[5],如果有就使用,没有再使用 source 中的元素。用代码来描述这个通用过程就是:
const n =
const value = map[rIndex] ?? source[rIndex];
result.push(value); // 可以和上一句合并
map[rIndex] = map[n] ?? source[n];map 中保存了某个索引对应的修改后的值,所以每次去 source 中取值的时候,都先检查 map。如果 map 中有,就取 map 中的;map 中没有才去 source 中找。
说起来比较抽象,还是上图
相应的代码也就容易写出来了:
function randomSelect(source, m) {
const result = [];
const map = new Map();
for (let i = 0, n = source.length; i < m; i++, n--) {
const rIndex = ~~(Math.random() * n) + i;
result[i] = map.get(rIndex) ?? source[rIndex];
// ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
map.set(rIndex, map.get(i) ?? source[i]);
// ^^^^^^^^^^^^^^^^^^^^^^^
}
return result;
}
提示:这段代码可以和上一节最后一个 randomeSelect 代码对比着看。