Codeforces Round #774 (Div. 2)(ABCDE)

Codeforces Round #774 (Div. 2)(ABCDE)

总结：感冒十分难受，等等有时间写#775

A. Square Counting

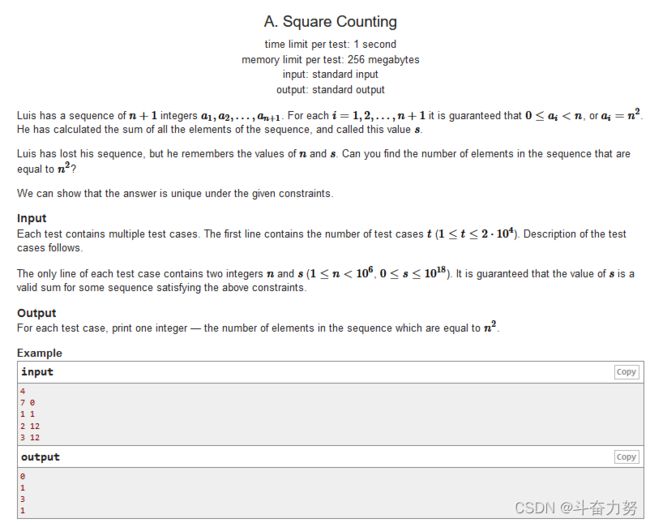
题意：给定两个整数n和s，表示有元素集合$\{1，2，3...,n\}\cup \{n^2\}$，用在集合中挑选n+1个数(可重复)组成s，问其中会有多少个$n^2$
思路：好像直接拿s/(n*n)就行了

#include
using namespace std;
typedef long long ll;
ll n,s;

void solve(){
    scanf("%lld%lld",&n,&s);
    ll n2=n*n,nu=s/n2;
    printf("%lld\n",nu);
}

int main(){
    int t;scanf("%d",&t);
    while(t--) solve();
}

B. Quality vs Quantity
题意：给定长度为n的序列，对其中数进行分类：红色、蓝色、无色。问是否存在情况，红色总和大于蓝色总和，同时红色个数小于蓝色个数
思路：从小到大排序，然后红色从后边取数，蓝色从前边取数，保证红色个数+1=蓝色个数，如果在使用个数<=n之前找到符号条件情况，就YES,否则NO。

#include
using namespace std;
typedef long long ll;
const ll N=2e5+5;
ll n,a[N],pre[N];

void solve(){
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
    sort(a+1,a+n+1);
    for(ll i=1;i<=n;i++) pre[i]=pre[i-1]+a[i];
    ll l=2,r=1;
    while(l+r<=n){
        ll nul=pre[l];
        ll nur=pre[n]-pre[n-r];
        if(nur>nul){puts("YES");return;}
        l++,r++;
    }
    puts("NO");
}

int main(){
    int t;scanf("%d",&t);
    while(t--) solve();
}

C. Factorials and Powers of Two
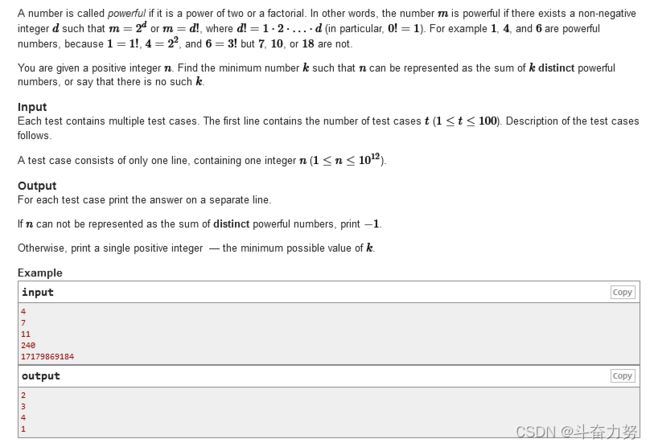题意：给定数字n，最少使用一些不同的元素构成n，可以使用的元素为某数的阶层或2的几次方。不能构成输出-1
思路：首先肯定能构成，因为给定的数一定可以转成二进制数，我们总可以用一些2的几次方构成该数。为了最少，我们可以先记录有多少数的阶乘小于n，数不多，可以进行二进制枚举选取情况，最后如果n还有剩余，就全部用2的几次方去补齐。

#include
using namespace std;
typedef long long ll;
ll n,ans,len;
vector<ll>num;

void init(){
    ll nu=1;
    for(ll i=1;;i++){
        nu*=i;
        if(nu>1e12) break;
        num.push_back(nu);
    }
}

ll go(ll x,ll state){
    ll ned=0;
    for(ll i=0;i<len;i++){
        if((state>>i)&1) x-=num[i],ned++;
    }
    if(x<0) return 1e9;
    return ned+__builtin_popcountll(x);
}

void solve(){
    scanf("%lld",&n);
    ans=__builtin_popcountll(n);
    len=num.size();
    for(ll i=0;i<(1<<len);i++) ans=min(ans,go(n,i));
    printf("%lld\n",ans);
}

int main(){
    init();
    int t;scanf("%d",&t);
    while(t--) solve();
}

D. Weight the Tree

题意：给定一颗由n个节点构成的树，一个好节点的定义是其值等于所有与其相邻的节点的价值和。
输出最多有多少好节点，在此基础上保证总价值最小，同时输出每个节点的价值
思路：树形dp，$dp[pos][0/1]$表示以节点u为根，节点u是坏/好节点的子树好节点树，同时因为有得到节点值，我们需要构造出来，所以同时记录一下节点u的代价。
特例：n=2，好节点个数2，总价值2，每个节点价值1
除特例外，好节点和好节点不可能直接相连，所以$dp[u][0]$可以从$max(dp[v][0],dp[v][1])$转移过来，而$dp[u][1]$只能从$dp[v][0]$转移过来。

#include
#define x first
#define y second
using namespace std;
typedef pair<int,int>PII;
const int N=2e5+5;
int n,w[N];
PII dp[N][2];
vector<int>edge[N];

void add(PII &a,PII b){
    a.x+=b.x;
    a.y+=b.y;
}

void dfs1(int u,int fa){
    dp[u][1]={1,-edge[u].size()};
    dp[u][0]={0,0};
    for(int i=0;i<edge[u].size();i++){
        int v=edge[u][i];
        if(v==fa)continue;
        dfs1(v,u);
        add(dp[u][1],dp[v][0]);
        add(dp[u][0],max(dp[v][0],dp[v][1]));
    }
}

void dfs2(int u,int fa,int type){
    if(type==0) w[u]=1;
    else w[u]=edge[u].size();
    for(int i=0;i<edge[u].size();i++){
        int v=edge[u][i];
        if(v==fa) continue;
        if(type==1) dfs2(v,u,0);
        else{
            if(dp[v][0]>dp[v][1]) dfs2(v,u,0);
            else dfs2(v,u,1);
        }
    }
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<n;i++){
        int u,v;scanf("%d%d",&u,&v);
        edge[u].push_back(v);
        edge[v].push_back(u);
    }
    if(n==2){
        puts("2 2");
        puts("1 1");
        return 0;
    }
    dfs1(1,0);
    if(dp[1][1]>dp[1][0]) dfs2(1,1,1);
    else dfs2(1,1,0);
    PII res=max(dp[1][0],dp[1][1]);
    printf("%d %d\n",res.x,n-res.y-res.x);
    for(int i=1;i<=n;i++) printf("%d%c",w[i],(i==n)?'\n':' ');
}

E. Power Board

题意+思路：

/*
一个n*m的网格，点(i,j)的值为i^j,问网格中一共有多少种元素
我们根据次方可知,例如i^4=(i^2)^2,所以我们可以只对所有的最简底数进行计算，看其有多少不同的指数
先得到最大指数是多少,随后化简底数形式，并遍历可能出现的情况，同时记忆化一下，因为当最大指数相同时，不同底数的贡献是一样的
例如底数x分别是2和3，两者初始的最大指数是3
x^1:    2    4     8     16              3    9    27     81    
x^2:    4    16    64    256             9    81   729    6561
x^3:    8    64    512   4096            27   729  19683  531441
发现不同底数，但当最大指数相同时，贡献都相同
*/

#include
using namespace std;
typedef long long ll;
const ll N=1e6+6,M=2e7+1; //pow(2,20)>1e6
ll n,m,sum,num[N];
bool vis[N];
int used[M];

ll go(ll x){
    if(num[x]) return num[x];
    ll nu=0;
    for(ll i=1;i<=x;i++){
        for(ll j=1;j<=m;j++){
            if(used[i*j]!=x){
                used[i*j]=x;
                nu++;
            }
        }
    }
    return num[x]=nu;
}

int main(){
    scanf("%lld%lld",&n,&m);
    for(ll i=2;i<=n;i++){
        if(vis[i]) continue;
        vis[i]=true;
        ll use=1,now=i;
        while(now*i<=n){
            use++;
            now*=i;
            vis[now]=true;
        }
        sum+=go(use);
    }
    printf("%lld\n",sum+1);
    return 0;
}