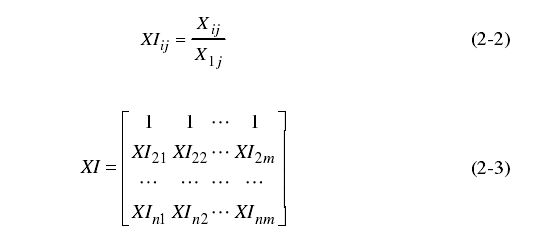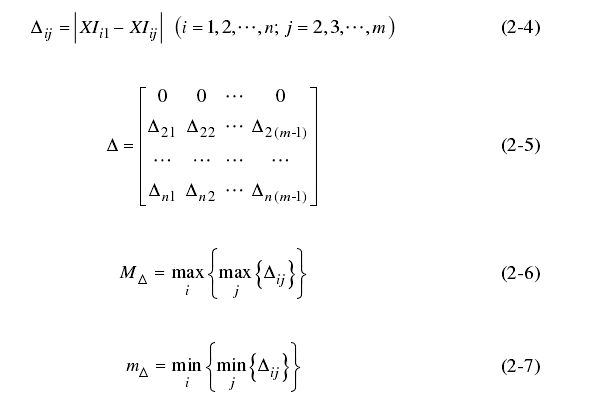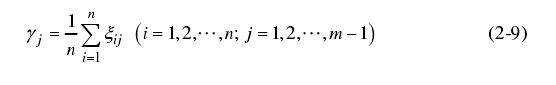灰色关联度分析法(GRA)_python
文章目录
-
- 定义
- 算法
- 标准
- 结论
- 例子
参考博客： GRA
定义
灰色关联度分析，是一种多因素统计分析的方法。简单来讲，就是在一个灰色系统中，我们想要了解其中某个我们所关注的某个项目受其他的因素影响的相对强弱，再直白一点，就是说：我们假设以及知道某一个指标可能是与其他的某几个因素相关的，那么我们想知道这个指标与其他哪个因素相对来说更有关系，而哪个因素相对关系弱一点，依次类推，把这些因素排个序，得到一个分析结果，我们就可以知道我们关注的这个指标，与因素中的哪些更相关。
算法
灰色关联度分析属于灰色系统的应用范畴分支，相比于常用的相关性分析法，其优势在于对分析样本的规律性与数量要求不高，适应性更为广泛。其思想是根据灰色关联度的大小来判断各影响因素与电力负荷特性的密切程度，从而确定哪些属于主要影响因素，哪些属于次要影响因素，避免预测时过多考虑次要影响因素而降低预测效率。总体分析流程如下：
（1）选择历史数据作为原始数据序列 X ，代表分析指标体系，如公式（2-1）所示，其中m为电力负荷特性及其影响因素的特征数量， n 为样本数量。
（2）为消除原始数据因单位不同而可能造成的干扰与误差，对原始数据序列根据公式（2-2）进行无量纲化处理，计算初值象序列 X I XI XI 如式（2-3）所示，其中 X I i j ( i = 1 , 2 , . . , n ; j = 1 , 2 , . . . , m ) XI_{ij}(i=1,2,..,n;j=1,2,...,m) XIij(i=1,2,..,n;j=1,2,...,m)为第 j 个指标的第i 个初值象。
(3）根据公式（2-4）求差值序列∆，计算差值序列如式（2-5）所示，并求得最大差 M ∆ M_{∆} M∆与最小差 m ∆ m_{∆} m∆分别如式（2-6）、（2-7）所示。
（4）根据公式（2-8）计算关联度系数序列 ξ \xi ξ ，其中 ρ ∈ ( 0 , 1 ) \rho \in(0,1) ρ∈(0,1)，此处取为0.5。
（5）利用关联度系数根据公式（2-9）计算关联度 γ \gamma γ，其中 γ > 0 \gamma>0 γ>0。
（6）根据关联度大小排列顺序，判断主要影响因素与次要影响因素。
（7）影响因素分析效果检验，包括确定指标体系时的数据检验、计算过程中公式及数据的检验、最终分析结果的检验。
标准
H为关联度
结论
GRA算法本质上来讲就是提供了一种度量两个向量之间距离的方法，以数学角度要言之，该算法即度量已归一化的子向量与母向量的每一维度的l1-norm距离的倒数之和，并将其映射到0～1区间内，作为子母向量的关联性之度量的一种策略。
例子
本节采用江苏省无锡市锡北镇的实际数据[59]，以年最大负荷 x 0 x_0 x0为要预测的电力负荷特性，以常住人口 x 1 x_1 x1 、人均收入 x 2 x_2 x2 、GDP x 3 x_3 x3 、农业总产值 x 4 x_4 x4、工业总产值 x 5 x_5 x5 、第三产业产值 x 6 x_6 x6、年平均温度 x 7 x_7 x7 、年降水量 x 8 x_8 x8、年售电量 x 9 x_9 x9为影响因素，用GRA分析各影响因素对负荷的影响程度。
注：母序列为最大负荷放在第一列，特征放在后面几列
最大负荷,常住人口,人均收入,GDP,农业总值,工业总值,第三产业产值,年平均温度,年降水,年售电量
21.2,6.8,3752,2.21,2.4,11.5,21,15.9,998.5,0.9
22.7,7,3897,2.78,2.43,11.8,22,15.6,995.2,0.98
24.36,7.15,4058,3.05,2.67,12.14,22.7,16.4,1002.6,1.1
26.22,7.28,4237,3.82,1.85,12.2,23,17.1,1237,1.23
28.18,7.42,4552,4.34,2.36,13,24.4,16.1,1170,1.36
30.16,7.55,4998,5.86,2.88,13.6,25.4,16.6,1001.3,1.49
86.6,10.23,22760,84.94,31,72,73,16.2,1232.5,5.41
-
代码
import pandas as pd data = pd.read_csv("data.csv") # 原始数据序列 X = data.values # 无量纲化处理 X = X / X[0, :] # 求差值序列 X = abs((X - X[:, 0].reshape(len(X), 1))[:, 1:]) M_delata = X.max() m_delta = X.min() rho = 0.5 # 求关联系数xi Xi = (m_delta + rho * M_delata) / (X + rho * M_delata) gamma = Xi.mean(axis=0) -
无量纲化
-
极差
-
关联系数矩阵ξ \xi ξ
-
最终关联系数γ \gamma γ
灰色关联度排序， x 6 > x 2 > x 9 > . . . > x 3 x_6>x_2>x_9>...>x_3 x6>x2>x9>...>x3，根据该值大小，可以看出 x 6 x_6 x6和负荷关联度最大， x 3 x_3 x3关联最小。