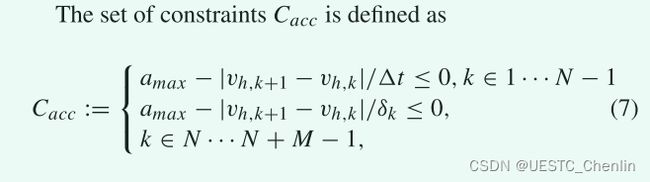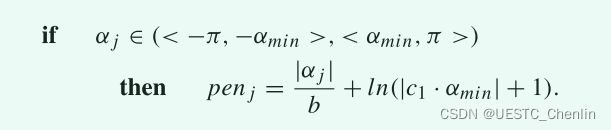【论文笔记】虚拟领导者控制编队机动

【名称】Formation control of unmanned micro aerial vehicles for straitened environments

【刊物】Autonomous Robots

【时间】2020.3

【单位】控制论系，电气工程学院，布拉格捷克技术大学，布拉格，捷克共和国

特点-不使用GPS，使用机载视觉进行相对定位。

摘要：本文提出了一种新的方法为控制和运动规划为多架无人驾驶微型飞行器（多旋翼直升机，在文献中通常也称为无人驾驶飞行器 - UAV 或无人机系统 - UAS）在杂乱无章的 GPS 拒绝环境中。 所提出的方法使我们能够在虚拟leader- follower方案中自主设计紧凑型微型飞行器 (MAV) 编队的复杂机动。 运动规划方法的结果和所需的编队稳定性是通过将虚拟leader与编队周围的hull(凸包)一起迁移来实现的。 这使我们能够在各个方向突然改变编队运动，独立于编队的当前方向，从而充分利用小型多旋翼直升机的机动性。 所提出的方法已经过验证，并且其性能已经在许多仿真和实验中利用一组 MAV 进行了统计评估。

关键词：Micro aerial vehicles · Motion planning · Virtual leader migration · Formation control

1.引言

        无人机（MAV）的控制和稳定性目前是一个深入研究的领域，因为其机动性高，能够到达地面移动机器人和固定翼无人机难以到达的位置。固定翼无人机通常更大，对于有障碍物的狭窄环境来说飞行速度太快。小型多旋翼微型飞行器尤其适合在这种杂乱的工作空间中应用，因为它们可以以相对安全的方式靠近障碍物，并且能够在较低的速度执行复杂的机动。多MAV飞行器系统的控制也需要同样的能力，在这种情况下，也需要解决密集编队飞行的微型飞行器的机间协调问题。

        在我们以前的工作中（马普林等人2019年），通过包括模型预测控制和轨迹规划，实现了单个MAV所需的高机动性。在本工作中，我们证明了MAV编队也可以通过单一的优化过程和采用沿着围绕编队的凸包hull迁移的虚拟leader概念来实现高机动性。经典的leader-follower方法的这种扩展使得编队的运动方向能够强制改变，通过周围环境中的障碍物，同时满足由leader-follower方法给出的要求，其中leader总是在编队的前面。这使我们能够依靠良好的leader-follower控制技术的理论，并保证群体的稳定性。为了能够在室内对MAV进行定位，我们依赖于我们在Krajnik等人(2014)的工作中描述的机载视觉相对定位系统。这个系统使我们能够估计编队中邻居的相对位置，通过提供的360度全景视图，通过由四个单目摄像机组成的环和由各编队成员携带的定位设备。(见图1）从检测到的图案大小及其在图像中的位置估计相对姿态。更新速率足够快，可以让我们将传感器直接集成到控制回路中。基于相机的分辨率和图案的实际尺寸，可以精确指定系统的感知范围（Faigl et al. 2013），并且可以转换为需要在轨迹规划和编队稳定中应用的约束机制。

         另一种用于验证提出的编队控制方法的技术依赖于紫外线LED的检测（Walter等人，2018年）。正如我们在沃尔特等人（2018）的工作中所展示的，这种方法使我们能够在光照条件变化的室外环境中可靠地稳定MAV编队。

        本文提出了一种新的运动规划方法和稳定的方式用于在杂乱的环境中控制紧凑编队中飞行的微型飞行器团队。该方法被设计用于基于视觉的机载定位技术。我们的主要贡献是：

1）所提出的方法侧重于在狭窄空间中部署空中机器人集群所需的关键特性，即有效的运动规划，能够自主设计复杂的编队机动，以及协调紧密编队飞行的大型 MAV集群；

2）对紧凑编队的操作以及在靠近障碍物的杂乱环境中的可部署性的要求，不使用全球导航卫星系统（GNSS），例如 GPS。  GNSS 不够精确，无法处理相邻 MAV 之间所需的相互距离，如果来自卫星的信号被障碍物部分或完全禁用则它们不是足够可靠；

3）本文是我们之前工作 Saska 等人 (2016)的扩展。 并且，在 GPS-denied 定位技术的一些最新进展之后，我们可以在这里展示一些真实的机器人实验；

        下述是文章的组织结构。第二节相关工作的介绍，第三节给出必要的条件，第四节聚焦MAV编队。第五部分展示数值仿真，硬件实验在第六部分，最后在第7部分总结。

2.相关工作

        机器人群编队控制和稳定性领域的研究目标涵盖了编队稳定化的主要领域，形成了期望的编队（董2011；亨斯特-莫弗里2010；刘和贾2012）和编队遵循预定义的路径，同时保持团队成员之间期望的形状和距离（DO和刘2011；Ghommam等人2010;Sira - Ramiandrez和CastroLinares，2010年；肖等人2009).其他的工作不希望有刚性的形状，而是一个适应的形状，以便最大限度的观察机器人团队（利马等人。2015).这种适应性也适用于避障（Nascimento等人2014)。然而，有几次，任何一种形式都必须为一个特定的目标而打破（Nascimento等人或改变编队的领导者（Tavares等人2019).

        在最近的队形控制研究中，队形leader位置的突然变化通常是通过在不同团队成员之间切换领导来实现的（Kwon et al.2015；Swaminathan et al.2015）。这种领导层转换的动机是提高系统的鲁棒性（Kwon等人，2015年），或使团队能够分成独立的子团队，以应对环境中的约束（障碍）(Swaminathan等人，2015年)。此外，导线火力编队控制中的切换机制用于应对互连拓扑的变化（Wang等人，2012年），改变各种控制策略（Ambroziak和Gosiewski，2015年），并在不同的期望形状之间重新配置编队（SperandioGiacomin和Hemerly，2014年）。所有这些工作都是在仿真中处理给定路径下编队的形状稳定性。Tavares等人（2019年）的工作提出了一种在控制层面的动态leader切换方法，但在轨迹规划中没有集成。相比之下，我们的重点是将虚拟leader的位置变换集成到轨迹规划进程中，以及对保持紧密队形的真正MAV部署的限制。

        （多旋翼直升机）的最新方法（Lee和Kim 2017；Shraim等人2018；L'Af Flitto等人2018；Loianno等人2017；Marzat等人2017）提出了用于控制微型飞行器编队，以及驱动固定翼无人机编队的方法（Liu等人2015；Kwonetal.2015）。在这些方法中，大多数都给出了编队要遵循的期望轨迹，或者通过根据编队要求修改的外部路径规划方法获得。只有在Garrido等人（2011）的工作中才能找到将轨迹规划与编队稳定过程相结合的方法，其中提出了一种将leader-follower方法与势场技术相结合的方法。然而，该算法是为地面完整约束机器人设计的，它存在着势场技术的常见问题，如局部极值附近的振荡、U形障碍物中的死锁，以及避免障碍物簇时的性能差。在这里介绍的方法中，我们能够包含有关环境的全局信息，这是Garrido等人（2011）的方法所不可能做到的。我们的方法还可以在充满障碍的环境中规划复杂的轨迹。 势场问题在编队控制中有许多不同的解决方案（Nascimento 等人，2014 年），但最近由 Dang 等人提出了一个解决方案（2019）去解决它。

        另一种方法是使用一致性算法。  Muñoz 等人的工作。 例如，(2017) 提出了一种基于分布式自适应leader-follower一致性算法的控制策略，用于受切换网络事件影响的多智能体系统 (MAS)。 该策略允许 MAS 中的每个agent根据本地信息和来自其邻居的信息计算自己的控制输入。 他们还使用交换网络拓扑方法扩展了一致性算法，以确保适当的性能。 他们进行了编队收敛实验来验证他们的方法。

        相比之下，我们建议在单个优化过程中将执行全局轨迹规划的能力直接集成到模型预测控制（MPC）技术中。MPC技术通常用于稳定具有控制约束的非线性系统，使我们能够集成编队中机器人的机动性约束、环境约束（无飞行区、障碍物）和相对定位约束，这些约束对GPS拒绝环境中的机器人部署至关重要，直接进入编队稳定过程。最近的MPC解决方案已证明，MPC方法可用于使用机载嵌入式处理器稳定单个MAV（Liu等人，2017年；Aoki等人，2018年）。虽然这些开创性的方法使我们只能实现简单的控制任务(比如在理想的无风条件下盘旋)预测范围可达10个过渡点，我们在之前的工作Baca et al.（2016）中展示了这一点，并在大量实验中验证了，使用嵌入式处理器和机载传感器，单个MAV的预测视界长度可以控制到200个过渡点。这使我们能够实现超过2秒的预测范围，这足以以多MAV场景所需的精度和稳定性跟踪任意动态变化的3D轨迹。这使我们能够提出并实验验证本文提出的轨迹规划和编队稳定系统。

        在我们的方法中，MAV部署在GPS拒绝和“运动捕捉拒绝”环境中的实际限制通过相对定位约束直接集成到轨迹规划和稳定方法中，通过螺旋桨气流的负相互影响，给出了MAV位置的运动约束和限制。没有必要将这些约束纳入设计用于仿真的方法中（Monteriu 2015；Kuriki and Namerikawa 2015；Mansouri et al.2015）。此外，如果没有真正的MAV实验，就不可能精确地确定这些限制。本文的重点是将小型微型飞行器群体的实际部署能力约束集成到基于MPC的运动规划与稳定系统中。它提出了一种方法，使我们能够实现编队的任意机动，从而在杂乱的工作空间中保持所需的形状。我们工作的这两个方面可视为本文的主要贡献。在新的MPC方法中，将期望目标的轨迹规划和即时编队控制集成到单个优化过程中。此外，虚拟follower相对于编队的位置在在轨迹被优化的的优化过程中同时被优化。由于这种内聚力，编队可以顺畅地响应其附近的变化，并且还可以在控制循环中考虑关于环境的全局信息。然后，本地控制输入不仅针对短期避障进行优化，而且针对编队的未来运动进行优化。这使我们能够在具有足够编队空间的部分工作空间中自主分配轨迹，并获得复杂的计划以在杂乱的环境中控制群体，同时保持用于相对定位的群体成员之间基于计算机视觉的技术的限制 。

3.动机和条件

3.1 问题定义

        本文研究了多旋翼直升机的编队控制问题。假设特定应用给出的期望形状满足所有编队成员相对定位的约束，即编队中任意两个机器人之间的最大距离小于机载相对定位系统的传感范围（Faigl等人2013；沃尔特等人2018)。MAV可以形成用于搜索和救援应用的搜索指形图，可以扩展以实现用于RFID定位的三角测量，可以形成用于拍摄应用的照相机-灯系统，或者可以形成用于运输的各种形状。编队的任务是尽可能精确地保持其期望的形状，但是如果环境需要临时变形是允许的(例如通过狭窄的走廊)并且由于followers的局部避障机动(例如由于团队成员的故障、动态避障、或避免碰上最近发现的障碍物）不能被包含leader的规划部分之内。

        假设有n个障碍物，在3d 中表示为复杂的多面体，位于工作空间中。在仅考虑多面体的情况下，基于gilbert-johnson-keerthi 距离算法(gjk) ，可以有效地得到障碍物与代表编队的凸形体之间的最小距离，该算法计算复杂度低，对于快速避障具有重要意义(gilbert 等，1988)。本文提出的实验依赖于 cameron (1998)描述的GJK算法实现。采用多面体表示工作空间中物体的假设来满足GJK方法的要求，但本文提出的方法允许将任意形状的物体视为障碍物。障碍物和目标区域在全局地图中表示，所有机器人共享这个地图。在任务期间，新的障碍可以添加到地图上，一旦他们被follower发现。此外，动态障碍物的位置，由机载传感器在地图上更新。用WIFI通信更新地图以及分发给followers期望轨迹。对于MAV定位，我们假设该系统仅依赖于机载传感器[IMU惯性测量单元、s向下看摄像头的光学流量——如PX4flow，以及相对视觉定位系统（Krajnik等人，2014年）]，并且没有外部定位系统可用。编队在环境中的全局位置可以通过任何机载全球定位相对不精确地获得（Scaramuzza等人，2014年）。在实验中，我们使用了Krajník等人（2010）的工作中描述的视觉导航，或者我们必须依赖由PX4flow-传感器获得的由速度积分出来的MAV位置。

3.2 模型预测控制

        模型预测控制的基本思想是利用系统的一个动力学模型来预测其未来的状态，并在一个具有恒定持续时间δl, l∈1 ,…, N的N个恒定控制元素的优化向量描述的短时间范围内对其控制进行优化。然后，最优化的控制输入的第一部分被用于引导机器人进入新状态。由于传感器和执行器的不确定性，机器人或多或少地偏离了预测状态。因此，从已实现的状态重新开始优化。更多有关MPC的详细信息可在ofMayne等人的工作中找到。 (2000).

        在我们先前关于控制地面机器人的工作中(Saska等人,2009)显示了，MPC预测horizon可以通过具有M个控制元素的附加规划horizon来扩展，M个控制元素具有可变持续时间δl、l∈1、…、N、N+1、…N+M。这种扩展使得我们能够将系统的即时控制和朝向目标位置的全局轨迹规划集成在一起。这种方法的优点是，在长期轨迹规划和编队局部控制中都使用同一个具有多约束的多目标优化。在这项工作中，考虑了以下目标：（1）到障碍物的距离，如果队形在安全距离处，则该距离为零，并且如果其变得更近，则该距离增加；（2）轨迹长度，作为轨迹过渡点之间的所有分段轨迹的长度之和获得；(3) 飞行时间，由所有段轨迹的时间间隔之和获得； (4) 与目标的距离，这对于规划过程收敛到均衡是重要的，即将轨迹的最后状态获取到期望的目标区域。此外，优化向量中收集的控制输入的值的约束被应用到优化过程中。这确保了结果有考虑到在编队中使用的MAV的运动能力。

3.3 曲线坐标系下的leader-follower方法

        在这里介绍的方法中，我们依赖于为地面车辆设计的leader-follower方法（Barfoot 和 Clark 2004），其中编队的形状在曲线坐标系中定义。 对于所提出的MAV编队控制系统，我们需要对该方法进行两次扩展。 除了明显需要扩展到 3D 环境（机器人在原始方法中仅限于 2D 平面）之外，我们还引入了一个能够突然改变其位置的迁移虚拟leader，这对于团队在杂乱的环境中的复杂机动至关重要。通过这种方式，我们充分利用了 Barfoot 和 Clark (2004) 方法的优势，该方法在保持MAV完整机动性的同时，使编队能够平滑和有弹性地移动。

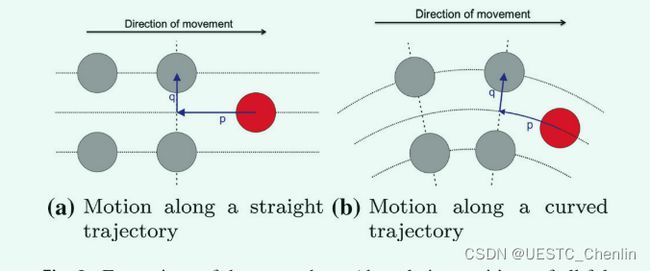
        让我们假设编队必须形成高度为hi的刚性形状。然后，MAV在编队中的期望位置由固定曲线坐标pi、qi和ri来定义，其中i={1····nr}，是相对于所提出方法中的虚拟leader的位置。坐标系的原点放置在表示虚拟leader在其当前位置的位置的点上。轴p是一条曲线，它沿着虚拟leader运动原点的方向追踪虚拟leader的路径（见图2）。轴q是一条水平线，它垂直于轴p。它定义了特定follower和虚拟leader在水平方向上的路径之间的距离。最后，轴r是一条垂直于轴p和q的线，它定义了虚拟leader和followers之间的高度差。一般来说，坐标pi、qi和ri可以在队形移动时改变，这些坐标定义了followers相对于虚拟leader的位置，从而确定队形的所需形状。机器人在不同形状之间过渡时的无碰撞协调由follower的控制机制来保证。然而，为了简化，本文只考虑了静态形状的编队。

图2： 沿不同轨迹的相同形状编队（所有followers的相对位置在两个示例中由相同的 pi 、 qi 和 ri 协调）描述

        为了在时间t将曲线坐标中的第i个followers的状态转换为笛卡尔坐标中的状态，可以应用以下方程：

 其中 PL(tpi ) 是领导者在时间 tpi 的位置。然后，可以使用已知的 p、q、r 坐标从虚拟leader的轨迹中获得所有followers的期望轨迹。

       在具有完美传感器和执行器的理想世界中以及在具有已知和静态障碍物的环境中, 由规划器驱动的虚拟leader的期望轨迹是可行的。对于特定followers来说。在具有不确定性的实际执行器和传感器的情况下，机器人可能偏离期望的规划，并且环境的当前地图可能不同于实际情况。因此，机器人可能会接近障碍物或彼此接近，这需要在每个follower的本地机载控制器中进行补偿。只有较短的控制范围需要优化，因为对环境的全局感知被包括在leader的轨迹规划中，并且follower只能对其附近的变化做出响应。在follower的轨迹规划中考虑以下目标，这些目标通常是对抗性的：①期望轨迹的偏差，这是从虚拟leader的轨迹获得的状态与所评估的轨迹的状态之间的差的总和；②编队中邻居的距离和到障碍物的距离，如果follower处于安全距离，则该距离为零，如果跟随者更接近，则该距离增加，和 (3) 控制输入中的振荡，作为优化向量中相邻控制输入的差的平方和获得。第三个目标用于减少控制编队中特定MAV所需的能量。此外，与虚拟leader的规划一样，在优化过程中，对优化向量中收集的控制输入值施加约束。这确保结果尊重特定follower的运动能力。

4.我们提出的方法

4.1 虚拟移动leader

        为了扩展编队的可操作性，在BarfootandClark  (2004) 的工作中使用的传统leader被虚拟迁移leader取代。可以在代表编队的凸壳的外圆上的任何地方初始化或重新初始化虚拟leader。这使得编队方向可以突然改变，在保持虚拟leader在编队前面的同时。在Barfoot&Clark  (2004) 提出的leader-follower方法中，假定队形的领导者总是位于队形的前面，follower跟随队形的运动。此概念可通过重新规划虚拟leader的轨迹来响应环境中的变化。然后，follower可以遵循虚拟leader的计划，并且队形在期望的形状中保持紧凑。如果一些follower在虚拟领导者前面，情况就不会是这样。

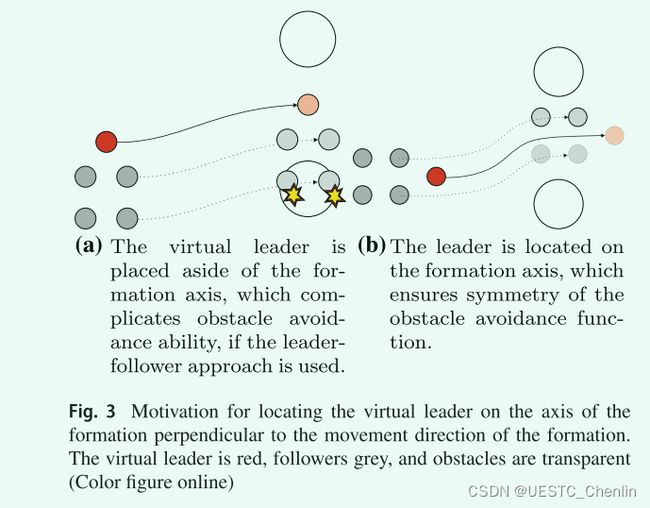
        此外，在我们的方法中，虚拟leader总是放置在外接圆和从其中心沿编队运动方向的射线的交点上。 这确保了虚拟leader沿其运动方向在编队的轴上飞行。 这个leader位置有利于在狭窄环境中进行有效的非碰撞轨迹规划，如图 3 所示。

         图4中示出了虚拟leader的偏移，以允许在编队的垂直方向上发生突然变化。我们描述了整个编队的轨迹，包括将虚拟leader的迁移作为一组控制输入使得编队突然变化，从队形的原始位置应用。在单个向量中的这种表示可以直接用作MPC方案中的优化向量。在向量中，表示在转向机动中转角改变的度数，表示切向速度，表示正常速度，是围绕旋转轴的角速度，是时间间隔。

         控制输入代表旋转角度，如图4所示，它允许解算器将机动动作整合到虚拟leader的轨迹中。α的极限为<−π, π >。如果α等于零，则不执行旋转，且编队继续以直射方式飞行。如果α不等于零，则执行旋转机动。机动本身包括以下步骤。

4.1.1 将编队悬停

        如果在编队运动的情况下执行旋转机动，则机动后可能出现不需要的剩余横向速度。为了消除剩余速度的可能性，需要使编队处于完全悬停模式。

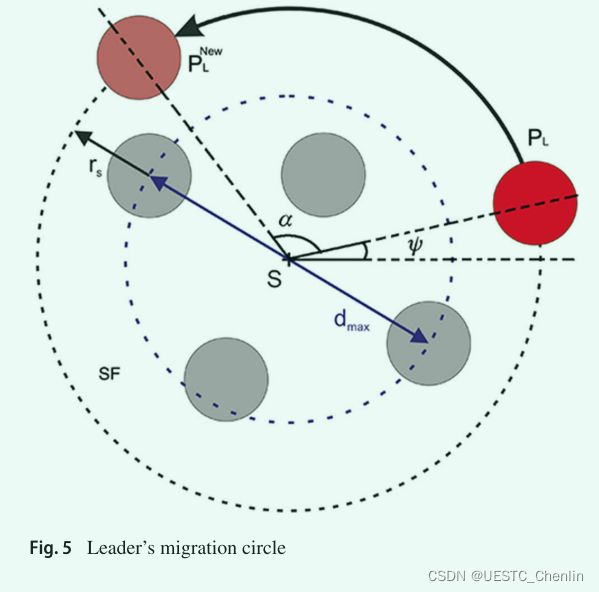
4.1.2 虚拟leader迁移

        一旦编队悬停，虚拟leader可以迁移到代表编队的凸包外接圆上的新位置（参见图 5 示例）。 为了能够定义leader的新位置，迁移圆的中心和半径由 Welzl (1991) 提出的算法解决的最小圆问题定义。  用作两个follower之间的最大相互距离，是附加的安全半径，用于确保leader始终在编队前面。

其中α是旋转机动的角度。

 

         四旋翼可以被认为是具有任何方向能力的全向飞行器。然而，MAV运动必须考虑用于避障和导航机载传感器给出的位置和方位，以及用于应用的执行器和传感器的位置（即用于环境监控的摄像机、无人机机械手等）。因此，重要的是，如果需要的话，能够保持MAV的heading角与其运动方向同步。

4.1.3 参数的重计算

        一旦leader迁移到新的位置，编队必须保持原来的形状，同时向新的方向飞行。 为了能够使用 Barfoot 和 Clark (2004) 定义的可靠的leader-follower方法，必须在leader迁移后重新计算原始参数 pi 和 qi。 为了保持队形的原始形状，第 i 个follower的位置（）为：

        坐标在转向机动期间保持不变， 参数的重计算如图6.

        虚拟leader在编队中迁移的算法如下:先让编队悬停，再根据轨迹的变化计算Leader的转角,然后迁移leader(根据)，然后计算现在followers的位置。计算新的，再根据新的算出follower下一步的位置。

4.2 虚拟leader的控制和运动规划

        编队从其当前状态到目标区域的总体轨迹可以编码为控制输入的矢量，如X，它在过渡点之间是恒定的。在每个规划步骤中，X作为MPC方案下的优化向量。从当前状态频繁地重新开始优化，因此仅将向量的开头作为优化的结果获得，用于MAV控制。向量X由垂直速度,水平速度,绕垂直轴(以虚拟leader的位置作为原点)的角速度,连续过渡点之间的时间间隔 δl (s)，以及编队航向旋转的角度 α (rad)

        正如引言中所提到的，我们提出将编队的短期控制及其轨迹规划与转弯机动结合成基于MPC的单一优化过程。在MPC技术中，从系统在一个时间间隔内的当前状态出发，求解系统的有限层最优控制问题，称为预测层。在此，我们将该方案扩展了另一个时间间隔（规划范围），具有M个额外的过渡状态。规划horizon在过渡状态之间具有可变的时间差，并且用于轨迹规划到期望目标区域。

        然后，我们将轨迹规划和编队控制解描述为成本函数 J(X) 的最小化，受约束集 、 和 的约束。 输入约束是

         和的极限由编队中的微型飞行器的运动能力给出。角速度受队形最小允许转弯半径的限制，该半径可确保所有follower以所需形状顺利移动。正如Barfoot和Clark（2004）所示，取决于编队的大小。这是L-F技术在有障碍物的杂乱环境中使用的主要瓶颈，有限的转弯半径降低了编队的机动性。解决这一局限性是提出迁移虚拟leader方法的动机。此外，极限取决于MAV的运动能力和所需的队形，因为如果，沿着外轨道的机器人比接近转弯中心的机器人走得更快（Barfoot and Clark 2004；Saska et al.2014）。

         约束确保距离从轨迹的最后一个点到目标区域的中心点小于半径。

        是编队在水平面的加速度限制。

        控制输入约束和加速度约束对于将旋转机动集成到轨迹当中非常重要。这些限制保证了在虚拟leader迁移之前停下，这是L-F方法的要求。多目标优化中用于控制虚拟leader的成本函数定义为：

         第一项是避障函数，如果轨迹(由应用于当前状态的运动模型的控制输入向量X描述)与障碍物之间的最小距离大于安全半径，则该避障函数为零。如果障碍物接近由安全半径定义的球体，则避障功能增加。由于所采用的视觉相对定位确保了follower之间的直接可见性，因此编队的球面表示是重要的。当障碍物接近避让半径时，J(X)的第一项的值变为无穷大。

        由于在预测范围内过渡态是以恒定的频率分布的，因此第二项的飞行时间惩罚仅取决于规划范围。这意味着由于缺少梯度，优化过程很难消除不必要的旋转机动，从而导致机动的消除。

        第三项惩罚运动振荡。这些振荡可能发生在MPC控制方案中，并且该项旨在保护系统免受控制输入中的非期望的偏差的影响。

        最后一项，旋转机动惩罚，惩罚转向机动。它可以用在优先选择没有转向机动的轨迹的应用中（其影响由常数 c1 设置），即使以较长时间到达目标为代价。在本文中，使用了该术语的非零权重 c1。惩罚项（在图 7 中可视化）被定义为：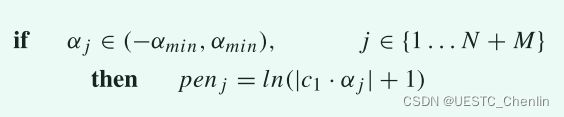

         对于任何大于的 α 值，惩罚几乎相同。然而，函数中仍有一个小斜率，以帮助求解器优化以消除不必要的操作。如果 α< ，旋转机动可以被轨迹曲率代替，大多数时候，取决于目标函数。因此，惩罚值开始显著下降，迫使求解器使用值 α = 0。

4.3 followers运动控制

        followers以我们先前工作中提出的成本函数为指导（Saska等人2014），可在机动过程中保持不变。下列人员的成本函数 由三个部分组成，由常数λi和σi (在本文的实验部分中设为λi = 1和σi = 1) 调整其影响：

         第一项用于惩罚从实际位置到的位置偏离。新位置是从使用迁移leader方法的虚拟leader规划的结果导出的。中的第二个项确保避免动态或最近检测到的障碍物。函数 提供了最近障碍物与跟随者轨迹之间的欧氏距离。的第三部分是回避功能的总和，其中团队的其他成员也被认为是动态障碍。这部分保护了邻居机器人在有意外行为发生时。函数返回第i个follower的规划轨迹与其他followers的规划轨迹的最小距离。最后，的形状允许followers重新定位，以避免障碍物、补偿执行器和传感器的不确定性，或避免邻居之间的碰撞。

5.数值仿真

        本节的目的是在各种编队飞行情况下，通过实验验证所提出的概念，并分析系统的性能。在实验（仿真和真实机器人）中，可行序列二次规划（CFSQP）库（Lawrence et al.1997）用于解决4.2和4.3中定义的优化问题。这些结果是通过Intel Core i7、2.4 GHz、4GB RAM实现的。

5.1 在狭窄通道中飞行

        第一个场景展示了本方法的主要贡献，即能够设计出在编队运动方向突然变化的复杂编队机动。这种行为使我们能够在杂乱的环境中充分利用MAV的运动能力，在这种环境中，由于障碍物，会强制执行群的急转弯。

        在仿真中，编队由四个follower组成，MAV用橙色轮廓表示。虚拟leader的位置由蓝色轮廓表示。在表1中总结了follower相对于虚拟leader的初始位置的期望曲线坐标。实验中的工作空间由具有三个90 °转弯的走廊组成。所需的编队尺寸和走廊宽度是这样选择的，即地层的最小转弯半径不能使其顺利通过走廊。

        需要对虚拟leader的位置进行突然更改的三种转弯操作在成对的快照中可视化（图8 b, c, e - h) 。在走廊的这些角落，编队被迫停止移动，虚拟leader的位置改变，并且编队沿着向量给定的方向从编队中心继续到虚拟leader的新位置。虚拟leader沿编队凸包的移动与整个轨迹一起被优化。。

5.2 光滑的斜坡状运动

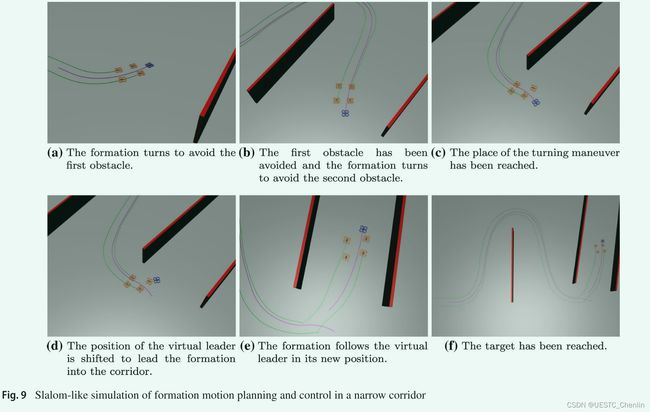
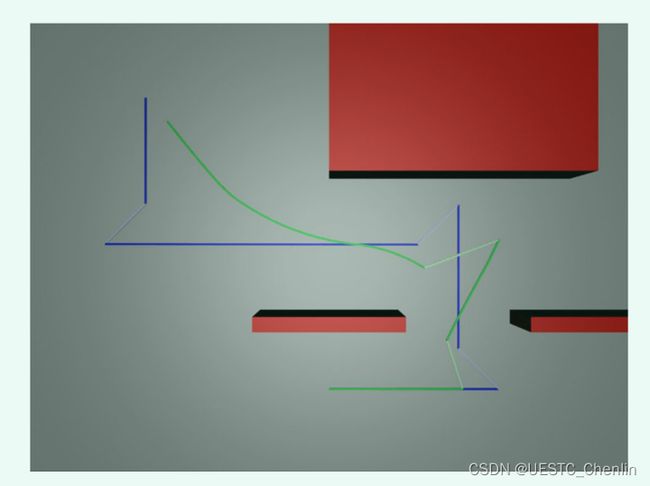
        另一个仿真，在图9f中，提出了系统在不充分开放的空间中规划平滑轨迹的能力，并在环境约束要求时自主地提出虚拟leader位置的改变。在仿真中，平滑地避免了第一个长杆障碍物，而不需要迁移虚拟leader（见图9 a, b) 。轨迹的最后一条曲线到达了目标区域，它位于第二个障碍物和第三个障碍物之间的走廊中，可以通过而不会突然改变运动方向，只是以延长轨迹为代价。根据成本函数 (8)，图 9c 所示的短机动轨迹 d 具有较低的代价，因此算法发现它是该运动规划问题的解决方案。

 5.3 具有大量 MAV 的编队飞行

        在系统性能的最后仿真中，使用10个MAV编队测试其可扩展性，参数总结在表2中。图10h显示了具有群体运动历史的实验概况。在仿真中，两种机动被要求导航编队穿过"门"到狭窄走廊中。在每个规划步骤中获得的解决方案的成本函数值的进展如图 11a 所示。 由于编队运动的速度恒定（轨迹在每个规划步骤中缩短大致相同的距离），成本线性降低，除了沿着虚拟leader位置位移的间隔，其中编队被迫停止。 在制动和随后在新方向上的加速期间，编队速度较慢，因此在这些间隔中成本值的下降也较小。 仿真过程中虚拟leader航向的进展如图 11b 所示。

        这种仿真忽略了在实际实验中观察到的和在以前的数值实验中模拟的上MAV的空气流对下MAV的影响。这使得我们能够验证系统稳定大型三维紧凑编队的能力。只有使用较小的MAV才有可能实现这种紧凑的3D形成的实际应用[如Kushleyev等人所示]。（2013）]与下一节实验使用的平台不同。        

 

    

5.4 统计分析

            在本节中，对该方法的可靠性进行了验证和统计评估。 此外，评估了成本函数 (8) 中旋转机动惩罚的各种权重的影响，以显示系统根据特定应用在平滑和更长的轨迹和包含转弯机动的较短轨迹之间进行选择的能力。 在规划过程中将机动包括到最终轨迹中的优先级由成本函数 (8) 中的参数 c1 设置。 在表 3 所示的实验中，评估了 7 组不同的参数 c1，每组在 300 个不同的场景中使用两个随机分布障碍物。 在每个场景中,初始位置,最初的轨迹,目标总是相同的,随机生成障碍的位置,这样最初的轨迹是可行的。

        为了评估算法的性能，飞行时间的平均值，旋转机动的数量，到障碍物的最小距离以及轨迹的曲率作为不同的算法设置在表3中被比较。 轨迹的曲率被测量为曲率的控制输入的绝对值之和乘以它们的持续时间。 如前所述，表中的每个值都是通过分析 300 次算法运行的结果获得的。 由于保证了初始解决方案的可行性，因此求解器能够在所有测试情况下找到可行的解决方案。 图 12 显示了这种生成场景的示例。

表3：权重c1在代价函数（8）中的影响，该函数惩罚解决方案中的旋转动作（缩写为man.）。在300个随机生成的场景中，测试了参数c1的每个设置

       

 图12.初始轨迹（蓝色）与在控制虚拟leader的第一个规划步骤中通过优化过程找到的轨迹（绿色）之间的比较。 初始轨迹中的第三次旋转机动在优化过程中被自动替换为平滑轨迹，解法中没有出现（在线彩图） 

        除了从统计集获得的平均值（表 3）外，分析结果还显示为图 13 中的箱形图，其中红线表示中位数，蓝色矩形的边缘是第 25 和第 75 个百分位数。胡须扩展到不被视为异常值的最极端数据点，这些数据点被单独绘制为红十字。如果点大于 q3 +w(q3 -q1) 或小于 q1 -w(q3 -q1)，则将点视为异常值，其中 q1 和 q3 分别是第 25 和第 75 个百分位数，w 是晶须长度。

        表 3 和图 13 中的分析证实，有可能影响最终轨迹包含编队速度突然变化的概率。通过这种方式，该算法可以适用于特定应用。转向机动的次数减少了重要性通过增加成本函数中机动惩罚项的权重。正如预期的那样，获得的轨迹的曲率随着机动次数的减少而增加。 此外，如果不使用转弯机动的轨迹是优选的，则轨迹与障碍物之间的最小距离会减小。 这两个因素显示了该方法在杂乱环境中的优势，在这种环境中，突然改变飞行方向的可能性使我们能够控制编队与障碍物的距离不足。 此外，可以更精确地实现更直的飞行，这也增加了解决方案的安全性。 当然，机动的可能性也可以处理不存在可行平滑轨迹的情况，如先前的仿真所示。

        在参数 c1 的设置和跟随轨迹所需的总飞行时间之间可以找到更复杂的相关性。 正如预期的那样，飞行时间随着机动惩罚的增加而增加，因为如果只选择直线飞行，则会获得更长的轨迹和更大的曲率。 然而，在 c1 较小的算法获得的统计数据集中也观察到了飞行时间的增加。 虽然惩罚最低的算法得到的轨迹最短，曲率最小，飞行时间会提高由于 MAV 被迫停止的机动次数。

 5.5 模拟拍摄历史建筑

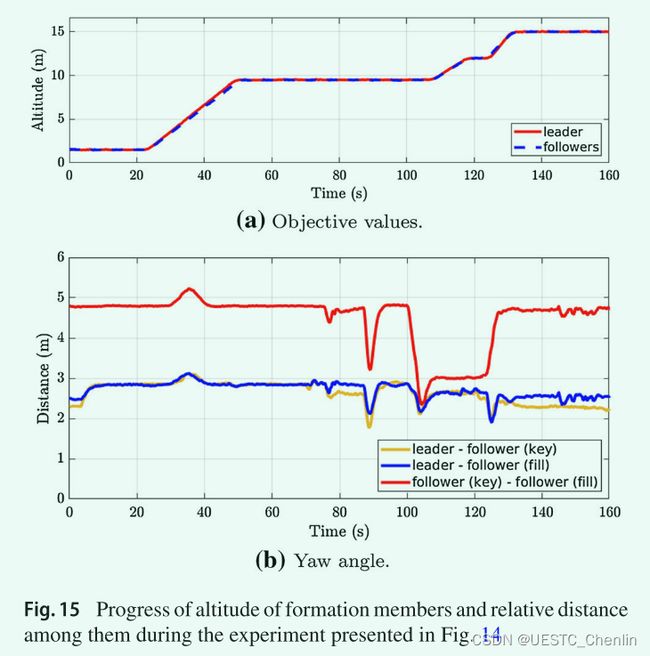
        图 14 中的仿真显示了所提出的编队飞行框架的应用。 我们使用一组 MAV 对历史建筑室内难以进入的地方进行自主记录和拍摄（有关教堂中实际部署的快照，请参见图 1 和 16）。 实验（图 14）旨在验证系统规划具有可变高度（z 坐标）的轨迹的能力，并在给定任务需要时改变编队形状的能力。 规划方法的这些能力没有包含在方法描述中以保持其理解，但它们的实施很简单。 在图 15 中绘制了该实验期间编队中机器人之间的高度和相对距离记录。在室内文档应用的情况下，编队的形状（相对于摄影师的距离和光线方向）和摄影机的高度取决于关于分配给拍摄对象的位置，以及三点照明技术的约束和要求（Zhang and Ma 2013;Birn 2014）。

图14：所提出的运动规划方法应用于自动留档和拍摄难以进入的历史建筑的智能照明任务（见图1）。上面的图片展示了编队的飞行，它由两个UAVillumator（光线方向由黄色锥体描绘）和一个UAV摄像师（其相机的视野以红色虚线为边界）组成，在一个有障碍物的环境中。编队的位置在不同的时间显示，无人机的轨迹由虚线描绘（摄影师-红色，照明器-蓝色和绿色）。摄影师在特定时间获得的照片如下所示（在线彩色图）

 

    为了强调这种智能照明方法的重要性，光源放置在远离相机的地方，让我们展示图 16 中的图片，这些图片是由携带相机和灯光的单个 MAV 捕获的（右上图 ) 并通过 MAV 编队，一个带有摄像头，另一个带有外部灯光（右下图）。 有关该算法的详细信息，该算法旨在为每个分配的对象提供最佳形状和所需的编队位置，请参阅Saska 等人的工作。(2017)。 本文提出的编队飞行算法，然后用于导航这些定义的所需位置之间的编队。 所需的编队位置是根据编队在整个建筑物地图中的位置顺序排列的。 通过应用具有方程(9)中成本函数的跟随者稳定方法来实现不同形状形状之间的过渡。

        

图16. Stara Voda 村的一座教堂的文件和勘探工作，该村是捷克共和国 Libava 军区和训练区的一部分。合作的 MAV 提供了一组教堂难以进入的部分和被捷克斯洛伐克士兵损坏的雕像的照片（  1968 年之前）和苏联士兵（1968 年之后）。 涂鸦的右上图是由一个同时携带相机和灯光的MAV拍摄的，而底部图片是由一对MAV拍摄的，一个带有相机，另一个带有外部光

6.真实实验

        在本节中，我们将介绍一些真实的机器人实验。实验使用了四个 MAV，每个 MAV 由一个 DJI hexacopter F550机架和 E310 DJI电机组成。这种选择满足了关于飞行时间和附加传感器所需的有效载荷能力的限制。该系统由 PixHawk 飞行控制器在最低级别进行控制，该控制器包含一组传感器，例如加速度计、陀螺仪和磁力计，这些传感器是无人机稳定飞行所必需的。Intel NUC-i7提供了必须的计算能力去解决机载图像处理任务、UAV协同任务、状态估计和运动规划任务。板载 PC 和 PixHawk 自动驾驶仪之间的消息使用 MAVlink 协议通过串行线路传输。 无人机之间的通信对于协调它们很重要，由嵌入在 PC 中的 WiFi 模块提供。 高分辨率 Mobius ActionCam 相机用于物体检测和相对视觉定位（见图 17）。 虽然该系统有一个 GPS，但它并没有在算法中使用。 它仅用作地面真值。 最后，所提出的解决方案依赖于机器人操作系统 (ROS)，这是机器人社区中常用的一组开源软件库和工具。

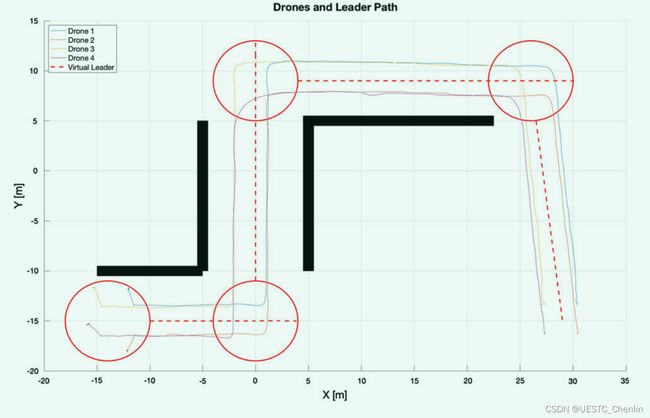
         在这个实验中，四个 MAV 必须遵循一个给定的轨迹，该轨迹只有在走廊每个角落的急转弯时才能进行转弯机动。 编队在狭窄通道内飞行需要编队速度的突变，才能在不与障碍物相撞、不相互碰撞的情况下绕弯飞行。 图 18 显示，无人机必须在编队内迁移该区域的虚拟leader。 红色圆圈代表该区域。 红色虚线是计划的虚拟leader轨迹。 两幅图都表明机器人不会相互碰撞，也不会与障碍物发生碰撞。

 图18.无人机编队轨迹的 XY 图。 四个圆圈代表虚拟leader可以迁移的编队周围的凸包。 在这个区域内，leader迁移，重新规划编队轨迹（彩图）

        图19显示了实验的3D情节和微型飞行器的路径。在这张图中，我们可以看到同一情节的两个视图。在这些视图中，我们可以注意到机器人以队形执行它们的路径，避开障碍物，避免相互碰撞。最后，真实机器人实验的顺序帧如图20所示。

 图19.4 架 MAV 编队在狭窄通道内飞行，需要突然改变编队速度才能在不与障碍物或其他 MAV 碰撞的情况下绕弯飞行

 图20.a实验从无人机处于初始位置开始。 b在leader迁移的情况下，编队进行第一个转弯，然后c进入第一个走廊。  d无人机队执行第二个转弯e保持编队。  f实验在路径的尽头结束

7.总结

        本文提出了一种新的运动规划概念，用于在高度混乱的环境中稳定微型飞行器的编队。所提出的方法基于沿编队周围的凸包迁移的动态虚拟leader。该方法是经过设计的，并已在仿真和真实机器人实验中进行了评估。这个概念适用于使用相邻 MAV 的机载视觉相对定位，这可以被视为在杂乱和 GPS 拒绝环境中部署大型无人直升机团队的技术。在所提出的方法中，优化了凸包上虚拟leader的位置，以及整个编队可行的整个轨迹。因此，该计划包括由周围环境和给定的任务强制执行的任意数量的编队机动，使 MAV 的运动能力得到充分利用。 此处介绍的方法已在各种复杂（室内和室外）工作空间中的大量实验和数值模拟中得到验证，并对其性能进行了统计分析。