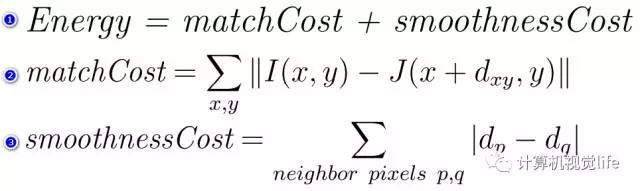双目立体视觉(双摄测距)
基于双目立体视觉的深度相机类似人类的双眼,和基于TOF、结构光原理的深度相机不同,它不对外主动投射光源,完全依靠拍摄的两张图片(彩色RGB或者灰度图)来计算深度,因此有时候也被称为被动双目深度相机。比较知名的产品有STEROLABS 推出的 ZED 2K Stereo Camera和Point Grey 公司推出的 BumbleBee。
ZED 2K Stereo Camera
1、为什么非得用双目相机才能得到深度?
说到这里,有些读者会问啦:为什么非得用双目相机才能得到深度?我闭上一只眼只用一只眼来观察,也能知道哪个物体离我近哪个离我远啊!是不是说明单目相机也可以获得深度?
在此解答一下:首先,确实人通过一只眼也可以获得一定的深度信息,不过这背后其实有一些容易忽略的因素在起作用:一是因为人本身对所处的世界是非常了解的(先验知识),因而对日常物品的大小是有一个基本预判的(从小到大多年的视觉训练),根据近大远小的常识确实可以推断出图像中什么离我们远什么离我们近;二是人在单眼观察物体的时候其实人眼是晃动的,相当于一个移动的单目相机,这类似于运动恢复结构(Structure from Motion, SfM)的原理,移动的单目相机通过比较多帧差异确实可以得到深度信息。
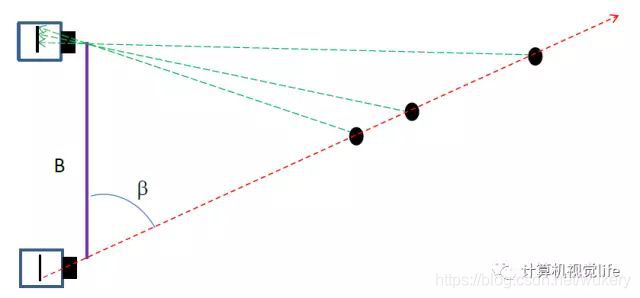
但是实际上,相机毕竟不是人眼,它只会傻傻的按照人的操作拍照,不会学习和思考。下图从物理原理上展示了为什么单目相机不能测量深度值而双目可以的原因。我们看到红色线条上三个不同远近的黑色的点在下方相机上投影在同一个位置,因此单目相机无法分辨成的像到底是远的那个点还是近的那个点,但是它们在上方相机的投影却位于三个不同位置,因此通过两个相机的观察可以确定到底是哪一个点。
双目相机确定深度示意图
2、双目立体视觉深度相机简化流程
下面简单的总结一下双目立体视觉深度相机的深度测量过程,如下:
1)、首先需要对双目相机进行标定,得到两个相机的内外参数、单应矩阵。
2)、根据标定结果对原始图像校正,校正后的两张图像位于同一平面且互相平行。
3)、对校正后的两张图像进行像素点匹配。
4)、根据匹配结果计算每个像素的深度,从而获得深度图。
欲知详情,且看下面详细介绍。
3、双目立体视觉深度相机详细原理
1)、理想双目相机成像模型
首先我们从理想的情况开始分析:假设左右两个相机位于同一平面(光轴平行),且相机参数(如焦距f)一致。那么深度值的推导原理和公式如下。公式只涉及到初中学的三角形相似知识,不难看懂。
理想情况下双目立体视觉相机深度值计算原理
根据上述推导,空间点P离相机的距离(深度)z=f*b/d,可以发现如果要计算深度z,必须要知道:
(1)、相机焦距f,左右相机基线b。这些参数可以通过先验信息或者相机标定得到。
(2)、视差d。需要知道左相机的每个像素点(xl, yl)和右相机中对应点(xr, yr)的对应关系。这是双目视觉的核心问题。
2)、极线约束
那么问题来了,对于左图中的一个像素点,如何确定该点在右图中的位置?是不是需要我们在整个图像中地毯式搜索一个个匹配?
答案是:不需要。因为有极线约束(名字听着很吓人)。极线约束对于求解图像对中像素点的对应关系非常重要。
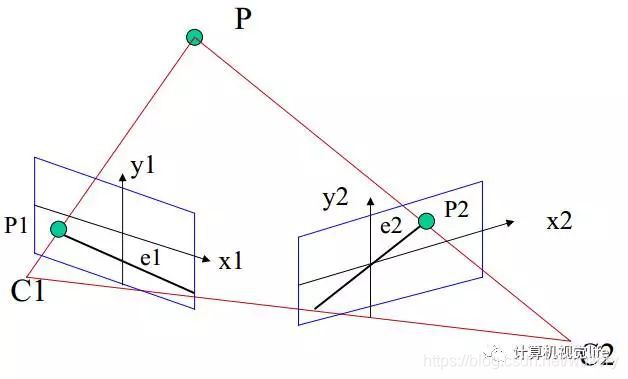
那什么是极线呢?如下图所示。C1,C2是两个相机,P是空间中的一个点,P和两个相机中心点C1、C2形成了三维空间中的一个平面PC1C2,称为极平面(Epipolar plane)。极平面和两幅图像相交于两条直线,这两条直线称为极线(Epipolar line)。P在相机C1中的成像点是P1,在相机C2中的成像点是P2,但是P的位置事先是未知的。
我们的目标是:对于左图的P1点,寻找它在右图中的对应点P2,这样就能确定P点的空间位置,也就是我们想要的空间物体和相机的距离(深度)。
所谓极线约束(Epipolar Constraint)就是指当同一个空间点在两幅图像上分别成像时,已知左图投影点p1,那么对应右图投影点p2一定在相对于p1的极线上,这样可以极大的缩小匹配范围。
根据极线约束的定义,我们可以在下图中直观的看到P2一定在对极线上,所以我们只需要沿着极线搜索一定可以找到和P1的对应点P2。
极线约束示意图
细心的朋友会发现上述过程考虑的情况(两相机共面且光轴平行,参数相同)非常理想,相机C1,C2如果不是在同一直线上怎么办?
事实上,这种情况非常常见,因为有些场景下两个相机需要独立固定,很难保证光心C1,C2完全水平,即使是固定在同一个基板上也会因为装配的原因导致光心不完全水平。如下图所示。我们看到两个相机的极线不平行,之前的理想模型那一套推导结果用不了了,这可咋办呢?
非理想情况下的极线
不急,有办法。我们先来看看这种情况下拍摄的两张左右图片吧,如下所示。左图中三个十字标志的点,在右图中对应的极线是右图中的三条白色直线,也就是对应的搜索区域。我们看到这三条直线并不是水平的,如果进行逐点搜索效率非常低。
左图中三个点(十字标志)在右图中对应的极线是右图中的三条白色直线
3)、图像矫正技术
怎么办呢?把不理想情况转化为理想情况不就OK了!这就是图像矫正(Image Rectification)技术。
图像矫正是通过分别对两张图片用单应(homography)矩阵变换(可以通过标定获得)得到的,的目的就是把两个不同方向的图像平面(下图中灰色平面)重新投影到同一个平面且光轴互相平行(下图中黄色平面),这样就可以用前面理想情况下的模型了,两个相机的极线也变成水平的了。
图像校正示意图
经过图像矫正后,左图中的像素点只需要沿着水平的极线方向搜索对应点就可以了(开心)。从下图中我们可以看到三个点对应的视差(红色双箭头线段)是不同的,越远的物体视差越小,越近的物体视差越大,这和我们的常识是一致的。
图像校正后的结果。红色双箭头线段是对应点的视差
上面讲到的对于左图的一个点,沿着它在右图中水平极线方向寻找和它最匹配的像素点,说起来简单,实际操作起来却不容易。这是因为上述都是理想情况下的假设。实际进行像素点匹配的时候会发现几个问题:
(1)、实际上要保证两个相机完全共面且参数一致是非常困难的,而且计算过程中也会产生误差累积,因此对于左图的一个点,其在右图的对应点不一定恰好在极线上。但是应该是在极线附近,所以搜索范围需要适当放宽。
(2)、单个像素点进行比较鲁棒性很差,很容易受到光照变化和视角不同的影响。
4)、基于滑动窗口的图像匹配
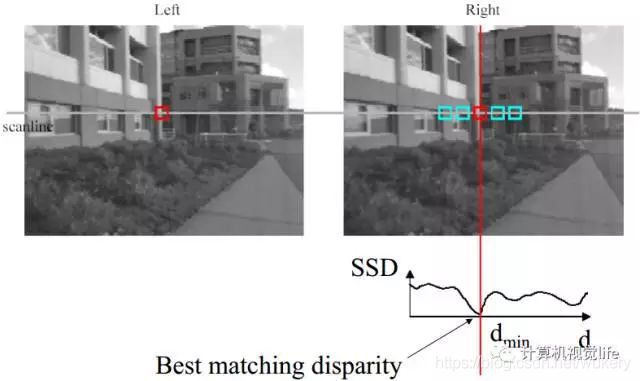
上述问题的解决方法:使用滑动窗口来进行匹配。如下图所示。对于左图中的一个像素点(左图中红色方框中心),在右图中从左到右用一个同尺寸滑动窗口内的像素和它计算相似程度,相似度的度量有很多种方法,比如 误差平方和法(Sum of Squared Differences,简称SSD),左右图中两个窗口越相似,SSD越小。下图中下方的SSD曲线显示了计算结果,SSD值最小的位置对应的像素点就是最佳的匹配结果。
滑动窗口匹配原理示意图
具体操作中还有很多实际问题,比如滑动窗口尺寸。滑动窗口的大小选取还是很有讲究的。下图显示了不同尺寸的滑动窗口对深度图计算结果的影响。从图中我们也不难发现:
小尺寸的窗口:精度更高、细节更丰富;但是对噪声特别敏感
大尺寸的窗口:精度不高、细节不够;但是对噪声比较鲁棒
不同尺寸的滑动窗口对深度图计算结果的影响
虽然基于滑动窗口的匹配方法可以计算得到深度图,但是这种方法匹配效果并不好,而且由于要逐点进行滑动窗口匹配,计算效率也很低。
5)、基于能量优化的图像匹配
目前比较主流的方法都是基于能量优化的方法来实现匹配的。能量优化通常会先定义一个能量函数。比如对于两张图中像素点的匹配问题来说,我们定义的能量函数如下图公式1。我们的目的是:
(1)、在左图中所有的像素点和右图中对应的像素点越近似越好,反映在图像里就是灰度值越接近越好,也就是下图公式2的描述。
(2)、在 同一张图片里,两个相邻的像素点视差(深度值)也应该相近。也就是下图公式3的描述。
能量函数
上述公式1代表的能量函数就是著名的马尔科夫随机场(Markov Random Field)模型。通过对能量函数最小化,我们最后得到了一个最佳的匹配结果。有了左右图的每个像素的匹配结果,根据前面的深度计算公式就可以得到每个像素点的深度值,最终得到一幅深度图。
4、双目立体视觉法优缺点
根据前面的原理介绍,我们总结一下基于双目立体视觉法深度相机的优缺点。
优点
1)、对相机硬件要求低,成本也低。因为不需要像TOF和结构光那样使用特殊的发射器和接收器,使用普通的消费级RGB相机即可。
2)、室内外都适用。由于直接根据环境光采集图像,所以在室内、室外都能使用。相比之下,TOF和结构光基本只能在室内使用。
缺点
1)、对环境光照非常敏感。双目立体视觉法依赖环境中的自然光线采集图像,而由于光照角度变化、光照强度变化等环境因素的影响,拍摄的两张图片亮度差别会比较大,这会对匹配算法提出很大的挑战。如下图是在不同光照条件下拍摄的图片:
不同光照下的图像对比
另外,在光照较强(会出现过度曝光)和较暗的情况下也会导致算法效果急剧下降。
2)、不适用于单调缺乏纹理的场景。由于双目立体视觉法根据视觉特征进行图像匹配,所以对于缺乏视觉特征的场景(如天空、白墙、沙漠等)会出现匹配困难,导致匹配误差较大甚至匹配失败。
纹理丰富(左)和纹理缺乏场景(右)
3)、计算复杂度高。该方法是纯视觉的方法,需要逐像素计算匹配;又因为上述多种因素的影响,需要保证匹配结果比较鲁棒,所以算法中会增加大量的错误剔除策略,因此对算法要求较高,想要实现可靠商用难度大,计算量较大。
4)、相机基线限制了测量范围。测量范围和基线(两个摄像头间距)关系很大:基线越大,测量范围越远;基线越小,测量范围越近。所以基线在一定程度上限制了该深度相机的测量范围。