最大流之二分图匹配

本文旨在对于个人知识的梳理以及知识的分享，如果有不足的地方，欢迎大家在评论区指出

---

在讲述今天的题目之前，需要先总结一下使用最大流解决问题的一个基本的思路:
首先我们假设问题的可行解为A，而我们通过建图求得的所有可行流集合为B，我们只需要证明A中的每一个方案与B中的每一条可行流一一对应，那么A中方案的最优解就与B中的可行流的最优解对应，其实也就是B中的最大流对于A中的最优方案

---

例题一: Acwing2175 飞行员配对问题

题目描述

第二次世界大战时期，英国皇家空军从沦陷国征募了大量外籍飞行员。

由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的 $2$ 名飞行员，其中 $1$ 名是英国飞行员，另 $1$ 名是外籍飞行员。

在众多的飞行员中，每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。

如何选择配对飞行的飞行员才能使一次派出最多的飞机。

对于给定的外籍飞行员与英国飞行员的配合情况，试设计一个算法找出最佳飞行员配对方案，使皇家空军一次能派出最多的飞机。

输入格式

第 $1$ 行有 $2$ 个正整数 $m$ 和 $n$。$m$ 是外籍飞行员数；$n$ 是皇家空军的飞行员总数。

外籍飞行员编号为 $1\sim m$；英国飞行员编号为 $m+1\sim n$。

接下来每行有 $2$ 个正整数 $i$ 和 $j$，表示外籍飞行员 $i$ 可以和英国飞行员 $j$ 配合。

文件最后以 $2$ 个 $-1$ 结束。

输出格式

第 $1$ 行是最佳飞行员配对方案一次能派出的最多的飞机数 $M$。

接下来 $M$ 行是最佳飞行员配对方案。

每行有 $2$ 个正整数 $i$ 和 $j$，表示在最佳飞行员配对方案中，外籍飞行员 $i$ 和英国飞行员 $j$ 配对。

如果有多种配对方案，则输出任意一种即可，方案内部配对输出顺序随意。

数据范围

$1<m<n<100$

输入样例

5 10
1 7
1 8
2 6
2 9
2 10
3 7
3 8
4 7
4 8
5 10
-1 -1

输出样例

4
1 7
2 9
3 8
5 10

解题思路

1. 分析题意: 题目的大体意思是一共有$n$个飞行员，其中外籍飞行员有$m$个，一个外籍飞行员可以唯一匹配一个皇家空军飞行员，问最大可以匹配多少对
2. 分析算法: 首先根据数据范围，我们可以首先想到解决二分图最大匹配的经典问题: 匈牙利算法(时间复杂度为$O(nm)$)，是ok的，之后我们尝试使用最大流来解决这个问题，最初我们考虑如何建图，这里建图的方式为我们设置一个源点$S$和汇点$T$，其中$S$连向外籍飞行员的所有节点，且边权为$1$，而皇家空军飞行员的所有节点则连向$T$，边权也为$1$，并且皇家空军飞行员与外籍飞行员之间也两两之间建边，边权为$1$，最终建立的图大致如下:
   
   建完图之后，我们需要证明两点，也就是刚开始描述的两点:
   • 对于本题中的一个合法方案，我们发现都可以对应上面流网络的一个可行流
   • 对于上面流网络的一个可行流，我们发现，因为边权要么为$0$，要么为$1$，所以对于外籍飞行员，它指向皇家空军飞行员的边只能有$1$条，因为可行流要满足流量守恒，所以对于可行流来说，也是可以对于该题的一个合法方案，由此，该方式就是可以求出原图的最大匹配的，还有一个问题就是我们的最大流不一定是整数，而这道题的边之间都为整数，那么会不会有我们的可行流集合太小不足以容纳所有的最优解的问题，这里参考算法导论的证明，由于dinic求最大流使用的都是int，故最大流是存在与整数集合中的，也就是说整数集合中包含最大流，至此证明完毕，使用该最大流的方式的时间复杂度为$O(\sqrt{n}\ast m)$
3. 解题代码

   import java.io.*;
   import java.util.*;
   
   class Main{
       
       static int N = 110, M = 5210, INF = 0x3f3f3f3f;
       static int[] h = new int[N];
       static int[] e = new int[M];
       static int[] f = new int[M];
       static int[] ne = new int[M];
       static int[] q = new int[N];
       static int[] cur = new int[M];
       static int[] d = new int[N];
       static int idx, s, t;
       
       static void add(int a, int b, int c){
           e[idx] = b;
           f[idx] = c;
           ne[idx] = h[a];
           h[a] = idx ++;
       }
       
       static boolean bfs(){
           int hh = 0; int tt = -1;
           Arrays.fill(d, -1);
           q[++ tt] = s; d[s] = 0; cur[s] = h[s];
           
           while(hh <= tt){
               int u = q[hh ++];
               for(int i=h[u]; i!=-1; i=ne[i]){
                   int v = e[i];
                   if(d[v]==-1 && f[i] != 0){
                       d[v] = d[u] + 1;
                       cur[v] = h[v];
                       if(v == t) return true;
                       q[++ tt] = v;
                   }
               }
           }
           return false;
       }
       
       static int find(int u, int limit){
           if(u == t) return limit;
           
           int flow = 0;
           for(int i=cur[u]; i!=-1 && flow<limit; i=ne[i]){
               int v = e[i];
               cur[u] = i;
               if(d[v]==d[u]+1 && f[i] != 0){
                   int t = find(v, Math.min(f[i], limit-flow));
                   if(t == 0) d[v] = -1;
                   f[i] -= t; f[i^1] += t; flow += t;
               }
           }
           return flow;
       }
       
       static int dinic(){
           int res = 0; int flow = 0;
           while(bfs()){
               while((flow=find(s, INF)) != 0){
                   res += flow;
               }
           }
           return res;
       }
       
       public static void main(String[] args) throws IOException{
           BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
           
           Arrays.fill(h, -1);
           String[] cur = in.readLine().split(" ");
           int m = Integer.parseInt(cur[0]);
           int n = Integer.parseInt(cur[1]);
           
           // 加边
           s = 0; t = n + 1;
           for(int i=1; i<=m; i++){
               add(s, i, 1);
               add(i, s, 0);
           }
           for(int i=m+1; i<=n; i++){
               add(i, t, 1);
               add(t, i, 0);
           }
           while(true){
               String[] arr = in.readLine().split(" ");
               int a = Integer.parseInt(arr[0]);
               int b = Integer.parseInt(arr[1]);
               if(a == -1) break;
               add(a, b, 1);
               add(b, a, 0);
           }
           
           System.out.println(dinic());
           for(int i=0; i<idx; i+=2){
               if(e[i]>m && e[i]<=n && f[i]==0){
                   System.out.println(e[i^1] + " " + e[i]);
               }
           }
       }
   }
   

---

例题二:圆桌问题

题目描述

假设有来自 $m$ 个不同单位的代表参加一次国际会议。

每个单位的代表数分别为 $r_i(i=1,2,\dots ,m)$。

会议餐厅共有 $n$ 张餐桌，每张餐桌可容纳 $c_i(i=1,2,\dots ,n)$ 个代表就餐。

为了使代表们充分交流，希望从同一个单位来的代表不在同一个餐桌就餐。

试设计一个算法，给出满足要求的代表就餐方案。

输入格式

第 $1$ 行有 $2$ 个正整数 $m$ 和 $n$，$m$ 表示单位数，$n$ 表示餐桌数。

第 $2$ 行有 $m$ 个正整数，分别表示每个单位的代表数 $r_i$。

第 $3$ 行有 $n$ 个正整数，分别表示每个餐桌的容量 $c_i$。

输出格式

如果问题有解，在第 $1$ 行输出 $1$，否则输出 $0$。

接下来的 $m$ 行给出每个单位代表的就餐桌号。

如果有多个满足要求的方案，只要求输出 $1$ 个方案。

数据范围

$1\le m\le 150$,
$1\le n\le 270$,
$1\le r_i,c_i\le 100$

输入样例：

4 5
4 5 3 5
3 5 2 6 4

输出样例：

1
1 2 4 5
1 2 3 4 5
2 4 5
1 2 3 4 5

解题思路

1. 分析题意: 这道题中可以看出不再像二分图的最大匹配那样一个点只可以匹配一个点，而是一个点可以匹配多个点，而题目的要求正是将不同单位的所有人数都分到各个餐桌上，使得同一单位的人在不同的单位就餐
2. 分析算法: 首先这道题已经不可以使用匈牙利算法来解决，我们可以直接考虑使用最大流来做，首先还是建图，我们可以这样来建，添加源点$S$和汇点$T$，单位和圆桌节点之间两两建立边权为$1$的边，而$S$与所有的单位节点建立边权为单位人数的边，所有的圆桌节点与$T$建立边权为圆桌可坐人数的边，大体如下图:
   
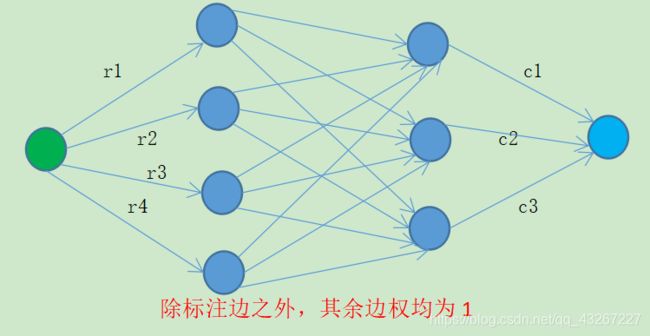
   之后我们需要证明两点:
   1. 我们可以发现，题目中的某一个合法匹配是可以对应上面流网络的一条可行流的，且是一条最大流
   2. 反过来，流网络的可行流也是可以唯一对应题目中的一个合法方案的，由于题目限制必须满流，所以我们最终需要判断可行流的流量是否等于总人数
   3. 解题代码

   import java.io.*;
   import java.util.*;
   
   class Main{
       
       static int N = 535, M = (150*270+N)*2, INF = 0x3f3f3f3f;
       static int[] h = new int[N];
       static int[] e = new int[M];
       static int[] ne = new int[M];
       static int[] f = new int[M];
       static int[] d = new int[N];
       static int[] q = new int[N];
       static int[] cur = new int[M];
       static int idx, s, t;
       
       static void add(int a, int b, int c){
           e[idx] = b;
           f[idx] = c;
           ne[idx] = h[a];
           h[a] = idx ++;
       }
       
       static boolean bfs(){
           int hh = 0; int tt = -1;
           Arrays.fill(d, -1);
           q[++ tt] = s; d[s] = 0; cur[s] = h[s];
           while(hh <= tt){
               int u = q[hh ++];
               for(int i=h[u]; i!=-1; i=ne[i]){
                   int v = e[i];
                   if(d[v]==-1 && f[i]!=0){
                       d[v] = d[u]+1;
                       cur[v] = h[v];
                       if(v == t) return true;
                       q[++ tt] = v;
                   }
               }
           }
           return false;
       }
       
       static int find(int u, int limit){
           if(u == t) return limit;
           
           int flow = 0;
           for(int i=cur[u]; i!=-1 && flow < limit; i=ne[i]){
               int v = e[i];
               cur[u] = i;
               if(d[v]==d[u]+1 && f[i] != 0){
                   int t = find(v, Math.min(f[i], limit-flow));
                   if(t == 0) d[v] = -1;
                   f[i] -= t; f[i^1] += t; flow += t;
               }
           }
           return flow;
       }
       
       static int dinic(){
           int res = 0; int flow = 0;
           while(bfs()){
               while((flow=find(s, INF)) != 0){
                   res += flow;
               }
           }
           return res;
       }
       
       public static void main(String[] args) throws IOException{
           BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
           Arrays.fill(h, -1);
           
           String[] cur = in.readLine().split(" ");
           int m = Integer.parseInt(cur[0]);
           int n = Integer.parseInt(cur[1]);
           
           // 加边
           s = 0; t = m + n + 1;
           int tot = 0; // 用于计算总人数
           String[] arr = in.readLine().split(" ");
           for(int i=1; i<=m; i++){
               int c = Integer.parseInt(arr[i-1]);
               tot += c;
               add(s, i, c);
               add(i, s, 0);
           }
           String[] tmp = in.readLine().split(" ");
           for(int i=1; i<=n; i++){
               int c = Integer.parseInt(tmp[i-1]);
               add(i+m, t, c);
               add(t, i+m, 0);
           }
           for(int i=1; i<=m; i++){
               for(int j=1; j<=n; j++){
                   add(i, j+m, 1);
                   add(j+m, i, 0);
               }
           }
           
           if(dinic() != tot){
               System.out.println(0);
           }else{
               System.out.println(1);
               for(int i=1; i<=m; i++){
                   for(int j=h[i]; j!=-1; j=ne[j]){
                       if(f[j] == 0){
                           System.out.print((e[j]-m) + " ");
                       }
                   }
                   System.out.println();
               }
           }
       }
   }