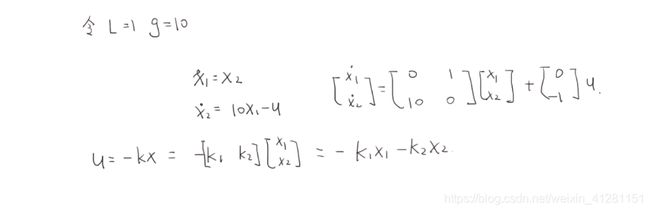LQR 控制学习-LQR控制 MATLAB官方教程-LQR 控制器_状态空间系统Matlab/Simulink建模分析
LQR 控制
本blog主要记录LQR 线性二次调制系统的,学习教程为两个B站的教学视频。
状态空间4-LQR控制 MATLAB官方教程
视频链接: [原创翻译]状态空间4-LQR控制 MATLAB官方教程
[原创翻译]状态空间4-LQR控制 MATLAB官方教程
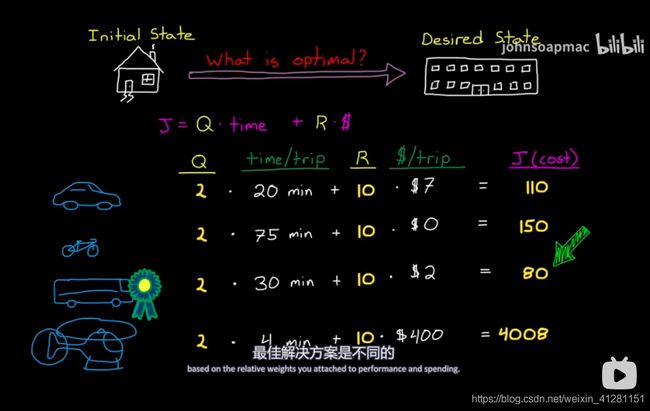
作者使用直白的例子去描述LQR的cost function Q为状态量的惩罚代价、R为推进器(输入)的惩罚代价,通过构建J 目标方程,以是的J最小的目的,求解K,从而得到最低成本下的增益矩阵。
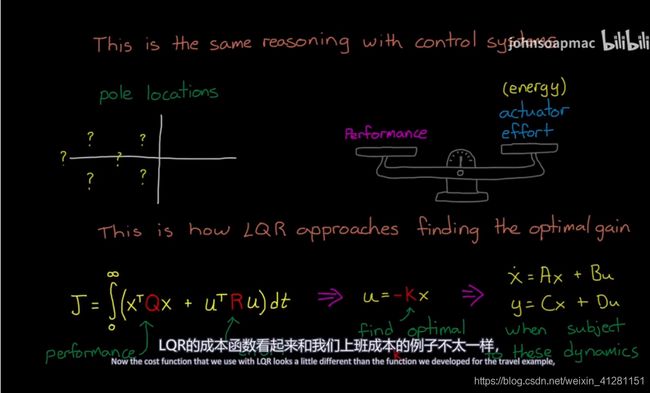
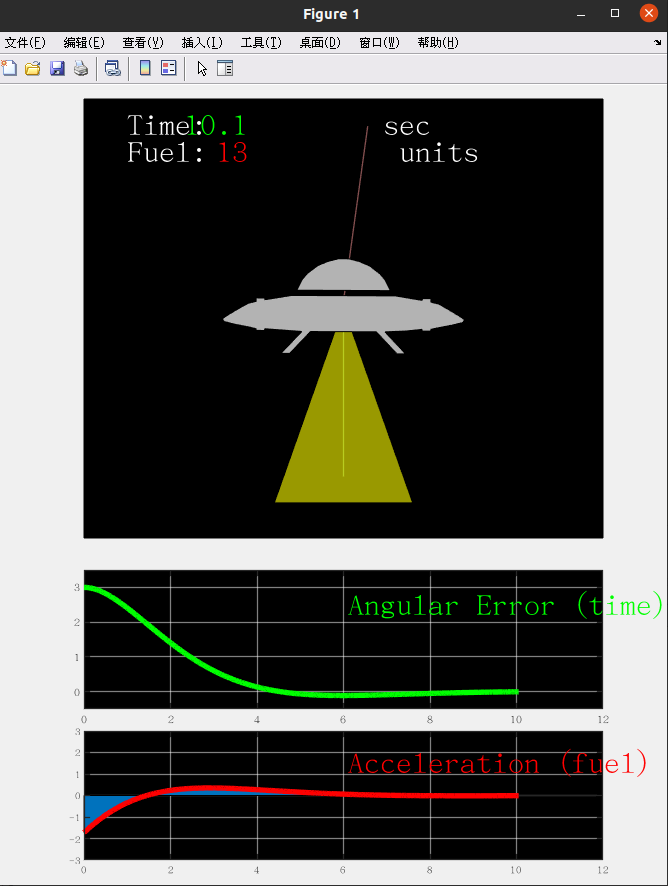
LQR-UFO实验:
matlab 官方代码
原视频网址
test1
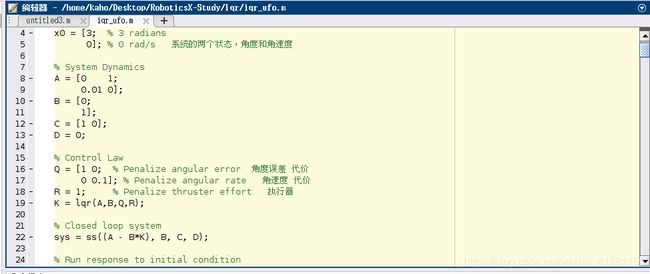
我们调节 Q矩阵,penalize angular error (角度误差代价) 为 1,penalize angular rate 为0.01 (角速度代价),角度误差代价比角速度代价要大得多。R = 1 (执行器输入代价)。
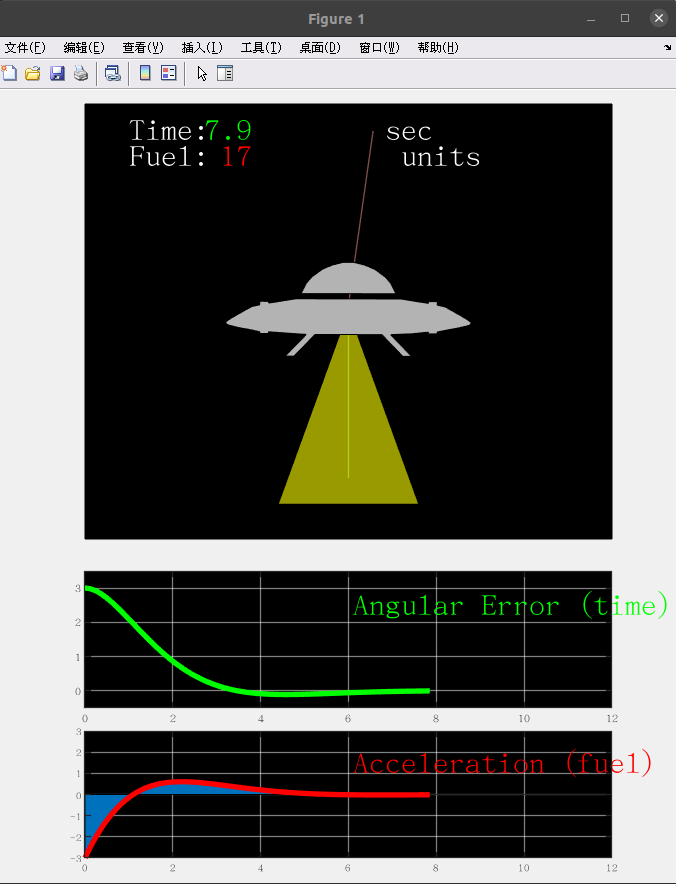
结果如下所示,在R penalize angular error 代价较大得情况下,使用lqr,Angular Error最后能收敛,并且没有出现较大幅度的超调。
test2
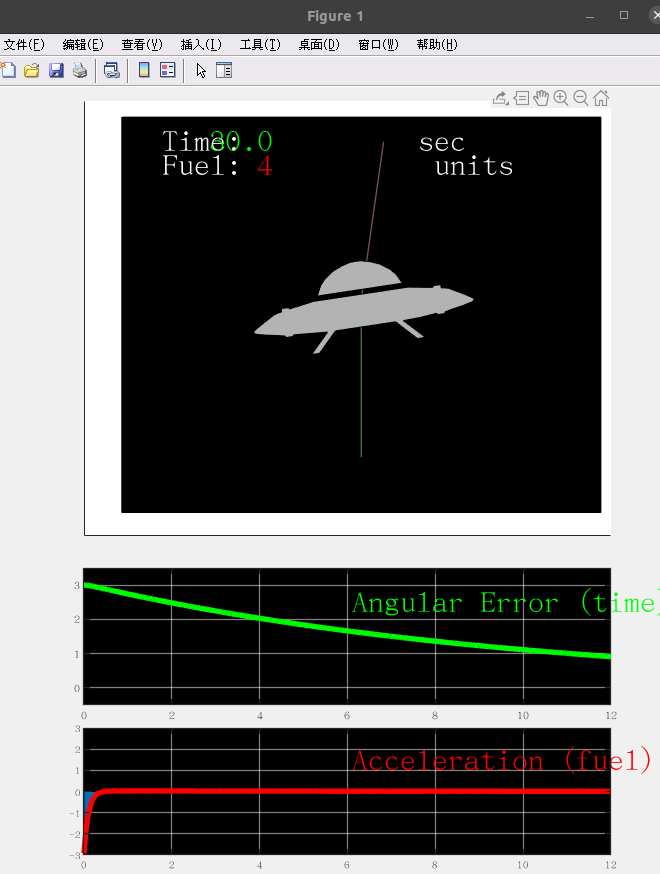
调节Q矩阵,penalize angular error (角度误差代价) 为 1,penalize angular rate 为100 (角速度代价)

结果如下所示,可以看到,加速度比较快的达到收敛,并趋于稳定,但相应Angular Error没办法保证收敛。
test3
调节R矩阵 Penalize thruster effort 执行器代价为3

结果如下所示,燃烧的燃料明显少了
【Advanced控制理论】8_LQR 控制器_状态空间系统Matlab/Simulink建模分析
视频链接:【Advanced控制理论】8_LQR 控制器_状态空间系统Matlab/Simulink建模分析
【Advanced控制理论】8
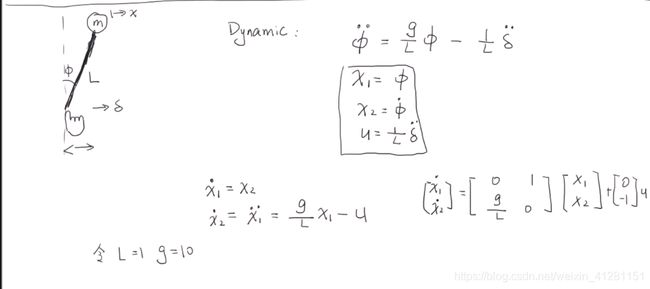
先上公式
先上公式
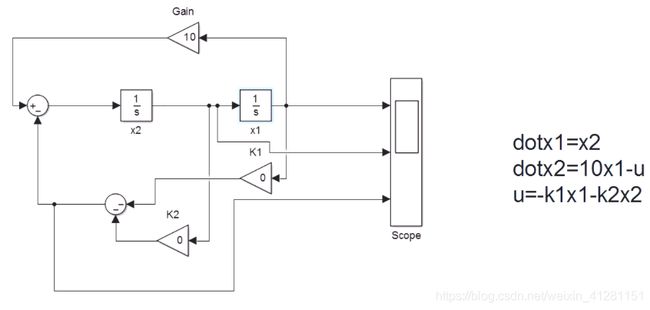
test1 开环系统
simulink 仿真模型下载
设置K1 、K2 = 0,使用scope检测开环系统下 ,x1 位移;x2 速度;u 负反馈输入
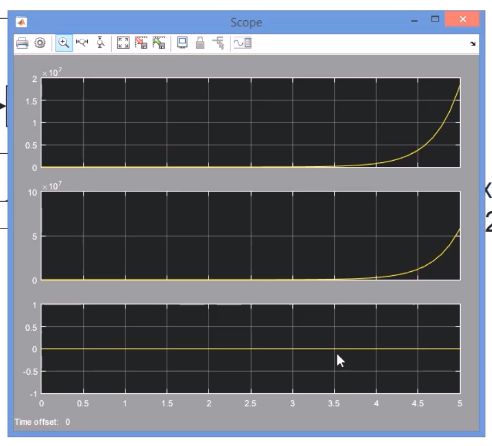
如下所说,可看到,在开环系统下,x1 x2趋向发散
test2 加入负反馈输入,构建闭环系统,lqr求解参数K
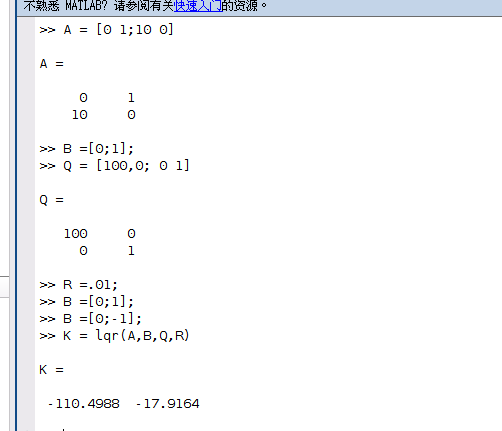
将通过自行设置的Q R,求解出的K,写进simlink中的k1 k2
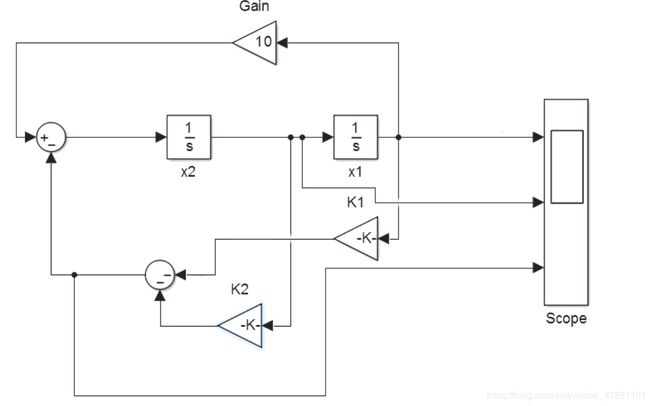
结果如下所示,可看出加入闭环系统后,x1 x2 都趋于收敛
test3 修改R,对照实验
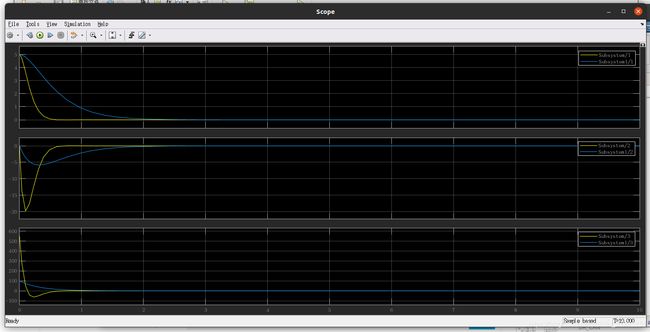
将整个闭环封装成三输出的Subsysytem,进行对照实验
将Q矩阵设置为单位阵,R(执行器代价) 设置为原来的100倍,R = 10,并将计算出来的K1、K2输入到中,观察scope输出
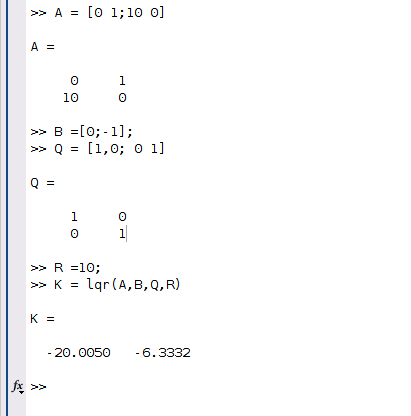
对比结果如下所示,黄色为上述test2的实验结果,蓝色为test3的实验结果,如下图所示,scope1中黄线的收敛速度明显比蓝线要快,如scope3所示,当提升了R的损失权值后,输入(蓝线)要更平稳一些。对于两个系统来说,最终结果都是一样的,最后都实现了状态的收敛。对于黄线来说,我们更看重的是收敛的效果、响应速度,而对于蓝线来说,我们更看重的是能耗问题。