强化学习之DQN算法实战（Pytorch）

之前在博主另一篇关于Q-learning算法：https://blog.csdn.net/MR_kdcon/article/details/109612413 ，DQN算法是基于Q-learning算法的，关于Q-learning有兴趣的可以看一看，欢迎指出不足之处。

和上一篇Q-learning算法一样，本文也将以2个实例来学习DQN算法。

DQN（Deep Q-Network） 是强化学习与深度学习的一个结合，即将Q-learning算法与深度网络进行联合，从而让智能体agent进行学习。DL为agent提供学习的大脑，RL提供了计算机制，从而达到真的AI。

关于DQN可参考：https://zhuanlan.zhihu.com/p/21421729

 

实战内容：

1、小车爬坡实验

2、小车平衡杆实验

所需包：torch、gym、pandas、matplotlib、numpy

pytorch官网：https://pytorch.org/

gym官网：http://gym.openai.com/

开发环境：pycharm

 

 

一、实际效果：

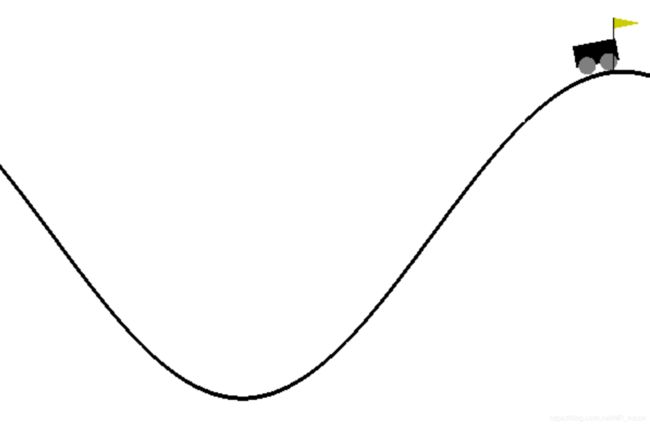
小车爬坡实验：

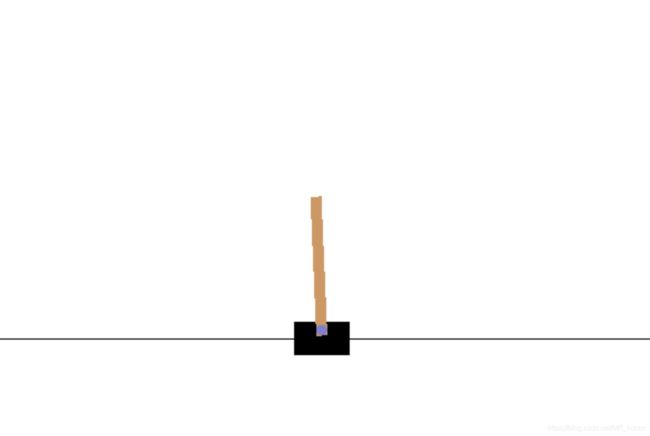
平衡杆实验：

 

 

 

 

二：DQN算法：

2.1、伪代码

首先来一波论文率先提出的伪代码：（下图是2013年提出的第一代NIPS DQN，2015年在原有基础上增加了Target-Q-network，就是下面翻译部分）

 

 

2.2、升级版翻译

翻译一下：（2015年Nature DQN算法）

1、初始化参数N（记忆库），学习率lr，贪心策略中的，衰减参数，更新步伐C

2、初始化记忆库D

3、初始化网络Net（本实验选择一个2层的网络，其中隐藏层为50个神经元的FC层），将参数W和W_指定为服从均值为0，方差为0.01高斯分布，并例化出2个相同的网络eval_net(以下简称Q1)和target_net(以下简称Q2)。

4、for episode in range(M):

5、     初始化状态observation

6、     for step in range(T):

7、            通过贪心策略选中下个动作action，其中Q(s, a)来自于eval_net的前向推理。

8、            通过环境的反馈获得observation'以及奖励值reward。

9、            将observation、observation'、action、reward打包存入记忆库D中。

10、          当记忆库存满之后，抽取batch个大小的数据(sj, sj', aj, rj)送入2个网络中

11、          以损失函数L =  *( rj +  * max(Q2(sj';W_)) - Q1(sj,aj;W))^2 进行训练

12、          每隔C步，更新target_net的参数W_ = W

 

下面这张博主画的图可以很好实现上述的伪代码过程：

 这里需要注意的是，target_net是不需要参加训练的，其参数的更新来源于eval_net的复制。

 

 

2.3、DQN提出的原因：

Q-learning算法，使用Q表来存储动作状态值函数，通过不断尝试来更新Q表，最终达到收敛，找到了最优策略。但是其缺陷在于Q表的容量和搜索范围，当一个任务的状态数目贼多，比如围棋、图像，那么对Q表的存储量是个考验，此外，搜索也是个问题。另一方面，若任务的状态值是个连续值，比如接下去的小车位置、速度，Q表是不够用的。因此需要用值函数近似的方法，用一个非线性函数去拟合动作状态值函数，达到升级版Q表的角色。拟合这件事neual network就很擅长，输入是个状态，输出则是状态对应的各个动作的值，这不就相当于是Q表了吗，并且nn不怕你输入繁多的状态，也不怕你输入是连续值，故Q-learning将Q值存储的方式改成神经网络，那么DQN初步就形成了。当然DQN强大的原因，并不在于此。

 

2.4、DQN强大的原因：

2.4.1、引入经验池：就是用一个二维数组将过去的样本存储起来，供之后网络训练用，具体来说，经验池的引入：

a、首先Q-learning为off-policy算法（异策略算法，Sarsa为同策略，on-policy算法），也就是说，其生成样本的策略值函数更新的策略不一样，生成策略是-greedy 策略，值函数更新的策略为原始策略。故可以学习以往的、当前的、别人的样本。而经验池放的就是过去的样本，或者说过去的经验、记忆。一方面，和人类学习知识依靠于过去以往的记忆相吻合，另一方面，随机加入过去的经验会让nn更加有效率。

b、打乱样本之间的时间相关性。回顾nn中输入样本之间是无关的（除了RNN比较特殊），随机性抽取有利于消除输出结果对时间连续的偏好。

c、每次抽取batch个数据正适合nn的前向和后向传播。

 

2.4.2、引入Target-Q-network

a、这个网络的输出通过取max，乘以，加上reward，作为标签y。这是由于Q-learning是值迭代算法，r +  * max(Q2(s_,a')是target Q，与Q-learning一样，DQN用这个作为标签，让Q（s，a）去无限接近标签，从而找到最优策略。

b、延迟更新网络。第一代的NIPS DQN是和Q（s，a）同时更新的，这就使得算法的稳定性降低，Q值可能一直就靠近不了target Q，但也不能不变，比如Target-Q-network刚初始化后，其产生的Q（s',a'）是不准确的，就像Q-learning中Q（s',a'）由于刚开始时候，也不住准确，都是0，但接下去会不断更新Q表，一段时间后，下一尝试同一个Q（s',a'）出现时，此时Q（s',a'）已经更新了，从第0次尝试->收敛过程中，Q（s',a'）一定是在不断更新，从0到最优值。因此Target-Q-network中的网络参数不能一尘不变，一段时间后，也需要更新。

c、另外，回顾下监督学习中，标签是个不随网路参数W变动的值，因此，一定时间内，需要维持不变，既为了稳定，又为了符合监督学习的特性。

 

 

 

三：代码解析（两实验代码大同小异，以小车爬坡为例）

3.1、环境说明：

3.1.1、小车爬坡实验：

 

对于外界的环境，我首先关注的就是其状态空间和动作空间。

其次需要关注的是环境的反馈：奖励值reward以及迭代停止的条件。

最后还需要知道初始化的状态。

note：这些我是直接参考gym的源码，每个实验都写的很清楚：http://gym.openai.com/

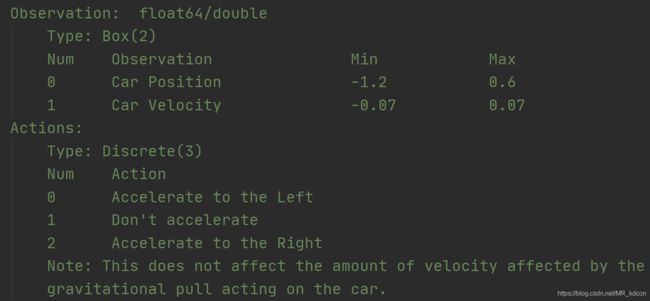
状态空间为space.Box类型的2个值，分别为小车的位置position和小车的速度velocity（向左为正，向右为负）

动作空间为space.Discrete类的3个值，分别为0（向左加速），1（不动）， 2（向右加速），需要注意的是，动作产生的加速是独立于小车重力产生的加速，即小车实际运动受到2个力，一个是自身产生的牵引力，另一个是自身重力，这里不考虑摩擦力。

奖励值：规定到达右边山顶奖励0，未到达不奖励。（很显然这个奖励机制需要后期更改）

迭代停止的条件有2个：1、小车的位置超出了0.5。（即旗子的位置）

                                      2、步伐超过200。（避免小车太墨迹）

初始化的位置：gym让小车每次reset：positon服从[-0.6，0.4]的均匀分布，且速度为0。

 

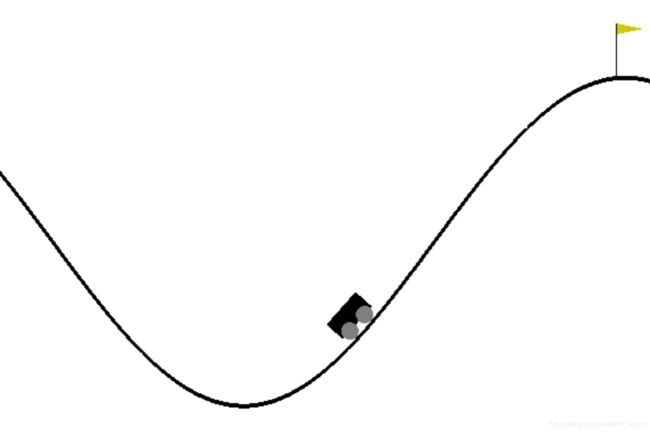
当然，最重要的是，该怎么设置奖励，或者怎么样去诱导小车实现爬坡呢？官方给的建议是让小车先跑到左边山坡，然后加速到达右边：

 

但是呢？我起初的直接想法是，小车否在初始化位置，直接向右加速到达山顶呢？答案是不能，经过测试以及源码中step函数的分析，小车在一直向右加速，只能到达半山腰的位置，然后就往下掉了，接下来是我的具体分析，有兴趣的可以看一看，也可以直接跳过，毕竟官方给过提示了。

 

为了检测这个想法的可行性

我设置了小车一直执行向右加速动作，最后显示结果，小车到达最远的位置是：

（可能是二手车，才这么点远。。。差不多position=-0.2）

哈哈哈，开玩笑，小车之后将往返循环运动，直到超出200步后，reset回到原位。

为什么呢？接下来我们看一下源码中step函数：这其实就是环境反馈函数，用于对当前给出的动作，给出环境对你当前奖励reward、下个状态、是否达到迭代结束条件。

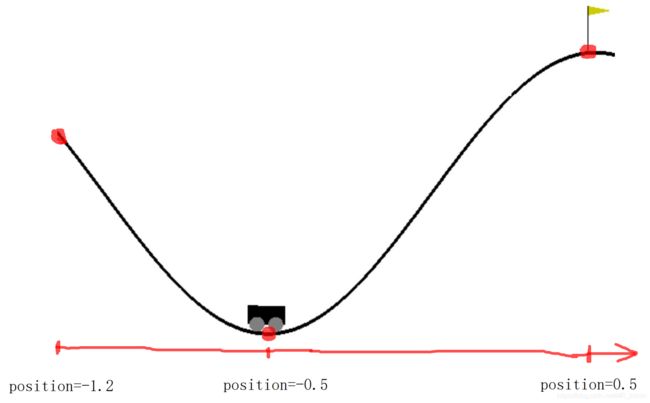
代码中第二行写得很清楚，小车的速度取决于牵引力force以及小车重力产生的速度，如下图图2所示。源码中self.force=0.001， self.gravity=0.0025，后者略大。

如上图所示，小车实际的环境是一个cos3x的函数，图中加粗部分为其实际运动位置。

关于速度和位置的值，其实就是牵引力force和重力gravity互相博弈的过程。

我们假设初始化为在postion=-0.5，初始速度为0，因为aciton=2，且根据上图图1，在-0.5附近，gravity的系数很小，以至于速度v大于0，然后更新positon，小车就会产生向右的动态。接下来的迭代过程，position会持续增大，速度也会持续增大，直到gravity前的系数大到让速度的更新为0，但此时position仍会继续增大，因为速度是正值，从而gravity开始占据优势，速度开始下降，但小车仍保持向前走。直到速度衰减为0，position不在增大。由于此时gravity占据绝对优势，因此速度开始为负，position开始下降，下车就开始往回跑了，保持加速的状态，但由于position越来越小，速度减小的幅度越来越小，直到减小幅度为0，同理，速度仍然是负值，position继续下降。接下去force占据优势，速度开始减小，但仍保持向左行驶，直到速度减小为0，postion开始不变，但此时速度的更新是正数，因此速度接下来变为正值，position开始增加，小车开始向右加速。。。就这么循环下去，直到达到退出条件为止，如上图图3所示。

上图是我截取的5次爬坡的实验数据，上面部分是小车在200步的迭代过程中位置变化，下面则是一一对应的速度变化，其变化过程和上述分析过程吻合。从图中可以看出，小车最多打大-0.2的位置，其速度就为0，因此可以得出结论，小车在初始位置时候是无法直接向右冲上去的。

不仅如此，我们也可以的出另一个结论：我们本次试验的开始速度都是0，那么若小车想要靠向右冲上去，显然其初始速度就要足够大，进一步可知小车必须进过左边小山坡的加速，才可以达到合适的速度，因此，小车必须自己学会跑上左边小山坡，然后向右加速到达山顶，这就是我们需要学习的策略，并且和官网给出的策略建议吻合。

 

note：5次曲线不一样是因为每次初始化都是随机的，其初始位置和初始速度不一样，因此曲线就会不一样。

 

3.1.2、小车平衡杆实验

接下来介绍拿到gym后，需要关注的几个参数：

状态空间： space.Box类，包含4个值，小车位置、小车速度、杆子偏离中心的角度，杆子角速度

动作空间：space.Discrete类，包含2个动作，小车向左和向右行驶。

奖励值reward：对于每一步，奖励值都是1。（显然需要重新分配）

终止结束条件：杆子偏离中心超过12°、或者小车位置超过+2.4或-2.4、迭代次数超过200次

初始状态：位置和偏离角度服从[-0.05,0.05]内的均匀分布。

 

当然了，最重要的还是如何重新奖励值，这直接影响了我们的策略。

显然我们需要小车尽快在最大步伐（200steps）限定内完成立杆。这需要满足2部分要求：

1、小车行驶的距离不要偏离中心太远。

2、杆子偏离中心的角度尽量要小。

满足这两个条件，小车就能尽快的平衡好杆子。

 

 

3.2、奖励设置

3.2.1、小车爬坡实验：

上图是我设置的奖励机制：对于-0.5--0.2区间内，奖励是position + 0.5，意味着初始位置奖励是0.

                                           对于-0.2--0.15区间内，奖励是position + 0.7，适当增加奖励，吸引agent更像往上走。

                                           对于-0.15--0.1区间内，奖励是position + 1，越高奖励越丰厚，适当增加奖励值。

                                           对于-0.1--0.5区间内，奖励是position + 1.2，越高奖励越丰厚，适当增加奖励值。

                                           对于-0.15--0.1区间内，奖励是0，对于左边不给奖励值。（这个地方可以再改进）

3.2.2、平衡杆实验

上图是我修改的奖励值，根据3.1.1中的分析，奖励取决于位置与偏离角度两方面，在中心往两边的过程中，逐渐减小奖励值。

 

 

3.3、主函数代码（只分析小车爬坡，平衡杆大同小异） 

env = gym.make('MountainCar-v0')  # 导入环境
dqln = dqn.Dqn()  # 包含DQN算法的一些函数和属性
finished_counter = 0  # 初始化完成次数
epochs = 1000  
finished_list = []  # 每50步记录一次50步内完成的次数，通过绘图显示DQN的训练成果

for epoch in range(epochs):
    observation = env.reset()  # array
    # episode_n = 0

    while True:  # 每一次迭代都是一步
        env.render()  # 环境更新
        # 选取动作
        action = dqln.choose_action(observation)
        # episode_n += 1
        # 获取环境反馈
        observation_, reward, done, info = env.step(action)  # observation_是个2元向量
        # 修改奖励值
        x, _ = observation_
        reward = x + 0.5
        if x >= -0.5:
            if x <= -0.2:
                reward = x + 0.5
            elif x <= -0.15:
                reward = x + 0.5 + 0.2
            elif x <= -0.1:
                reward = x + 0.5 + 0.5
            else:
                reward = x + 0.5 + 0.7
        else:
            reward = 0
        # 存储记忆
        dqln.memory_saved(observation, observation_, action, reward)
        # 2000容量记忆库每一步增加一条信息，因此10个200之后，才会开始学习
        if dqln.memory_num > dqln.N_memory:
            dqln.learn()
            if done:
                print(x)
                if x >= 0.5:
                    finished_counter += 1
                break
        # 存储满以后，这句话就不执行
        if done:  
            # print(episode_n)  # 200
            # print('记忆存储未满时，超过200步done=1')
            break
        # 状态更新
        observation = observation_
    if epoch % 50 == 0:
        finished_list.append(finished_counter)
env.close()

# 保存模型
torch.save(dqln.eval_net, './go_mountain.pth')
# 画曲线
plt.figure()
plt.plot(np.array(list(range(20))), np.array(finished_list), 'r', marker='o', linestyle='-', linewidth=2, label='t')
plt.legend(loc='best')
plt.show()

 

关于类的包装：

N_STATE = 2
N_ACTION = 3
class Net(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc = nn.Sequential(
            nn.Linear(N_STATE, 50),
            nn.Linear(50, N_ACTION)
        )

    def forward(self, x):


class Dqn(nn.Module):
    def __init__(self):
        super().__init__()
        self.eval_net, self.targrt_net = Net(), Net()
        self.targrt_net.load_state_dict(self.eval_net.state_dict())  # 保持初始参数一致

    def choose_action(self, s):  # 单个输入
    def memory_saved(self, s, s_, a, r):
    def learn(self):

 

3.4、注意事项：

1、其实我在上一篇https://blog.csdn.net/MR_kdcon/article/details/109612413 中说过，主函数的设计就是把上面DQN的算法描述出来，而需要的函数用类包装起来，这样也显得主函数更加简洁明了。

2、env.render()是进行图形渲染的函数，训练的时候需要将其注释，否则采样很慢。测试的时候取消注释看效果

3、DQN中target_net是不参与反向传播的，只有eval_net参与反向传播。

4、choose action函数的输入是单个状态，其通过eval_net的反向传播也需要被阶段，减少梯度计算。而训练的时候，输入eval_net是批量数据，毕竟对于神经网络来说，批量数据有利于增加计算速度以及在反向传播过程中综合了收敛速度和收敛方向的精确性。

5、gym返回的状态是个array数组。

6、在使用gym其他模型时候，要先去官网找相关模型的资料，率先关注状态空间、动作空间、奖励值、结束条件、初始化位置，并吸取官网给的决策建议修改奖励机制。

 

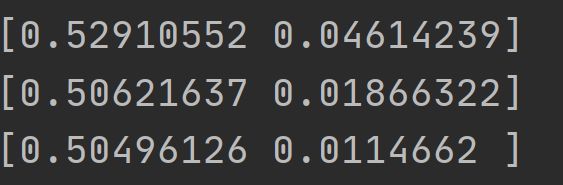
3.5、实验结果：

上图是训练一定次数后，小车爬坡连续3次都能上坡，数组的第0个值是位置信息，第1个值是对应的速度。 

下图是下车爬坡实验奖励修改前的奖励结果：也证明了这个初始奖励时不能用的。

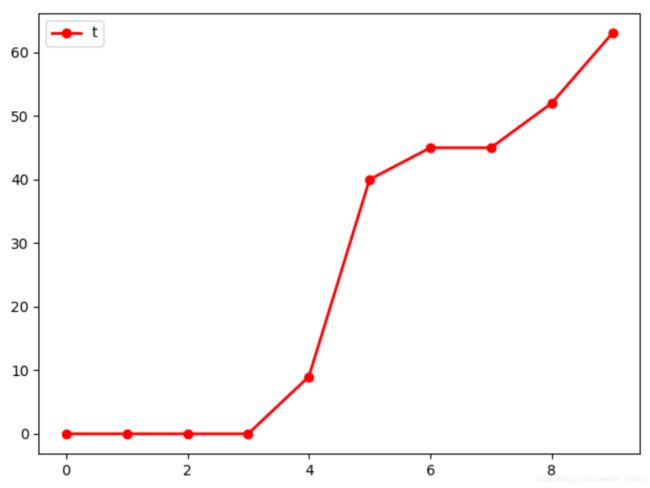
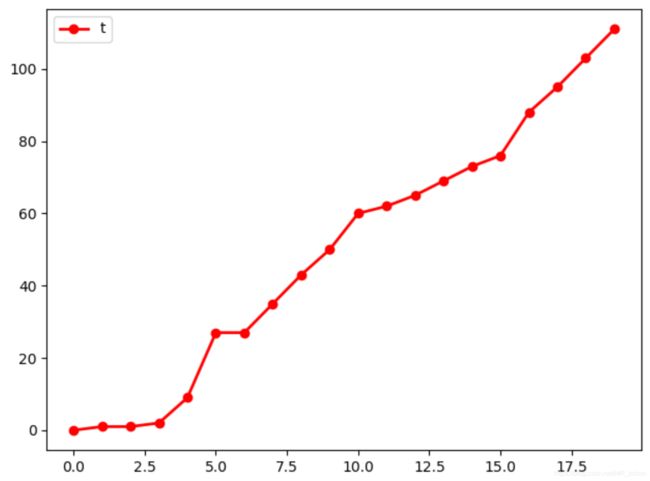
下面2张图分别是epochs=500和1000时候成功爬坡的记录图，分别完成了60次和120次，特别是训练后期，其完成次数开始不断增加，说明DQN的训练还是有效果的。 

 

 

小车立杆的效果和明显，几个epochs后就可以保持平衡立杆了。

 

 

四：总结

从小车爬坡实验中可以看出，DQN对于agent的学习还是很有帮助的，，但是训练的结果不如小车平衡杆以及之前的迷宫探宝一般准确，换句话说，当我将模型参数保存，进行inference的时候，小车爬坡成功的稳定性不高。这可能与设置的奖励机制还不够好有关，或者是神经网络的复杂度还不够，DQN的训练可以理解为是一个回归问题，因为模型不够复杂，因此不能够足够拟合数据。

因此有两个可以使得收敛成功率提升的方案：

1、改进奖励机制。

2、增加模型复杂度。

 

如果小伙伴们有更好的建议，欢迎留言或私信提出！