深度学习——tensorflow解决异或问题
异或问题
异或问题,简单说就是相同为0,相异为1
早在1969年时,感知机的流行,但还是不能解决异或问题,但在神经网络出现后,这个问题就被迎刃而解,加入隐藏层的神经网络就很好的解决了这个问题
数据如下
x = [[0, 0], [1, 0], [0, 1], [1, 1]]
y = [[0], [1], [1], [0]]
代码实现
import tensorflow as tf
import matplotlib.pyplot as plt
tf.set_random_seed(33)
x = [[0, 0], [1, 0], [0, 1], [1, 1]]
y = [[0], [1], [1], [0]]
X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])
w1 = tf.Variable(tf.random_normal([2, 3]))
b1 = tf.Variable(tf.random_normal([3]))
w2 = tf.Variable(tf.random_normal([3, 1]))
b2 = tf.Variable(tf.random_normal([1]))
z1 = tf.matmul(X, w1) + b1
a1 = tf.sigmoid(z1)
z2 = tf.matmul(a1, w2) + b2
a2 = tf.sigmoid(z2)
cost = -tf.reduce_mean(Y * tf.log(a2) + (1 - Y) * tf.log(1 - a2))
cost_history = []
m = tf.cast(tf.shape(X)[0], tf.float32)
dz2 = a2 - Y
dw2 = tf.matmul(tf.transpose(a1), dz2) / m
db2 = tf.reduce_mean(dz2, axis=0)
da1 = tf.matmul(dz2, tf.transpose(w2))
dz1 = da1 * a1 * (1 - a1)
dw1 = tf.matmul(tf.transpose(X), dz1) / m
db1 = tf.reduce_mean(dz1, axis=0)
learning_rate = 3.8 * 10e-2
updata = [
tf.assign(w2, w2 - learning_rate * dw2),
tf.assign(b2, b2 - learning_rate * db2),
tf.assign(w1, w1 - learning_rate * dw1),
tf.assign(b1, b1 - learning_rate * db1)
]
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(10001):
cost_var , _ = sess.run([cost, updata], feed_dict={X: x, Y: y})
if step % 500 == 0:
print('Step', step, 'Cost', cost_var)
cost_history.append(cost_var)
predict = sess.run(a2, feed_dict={X: x})
print('预测值为', predict)
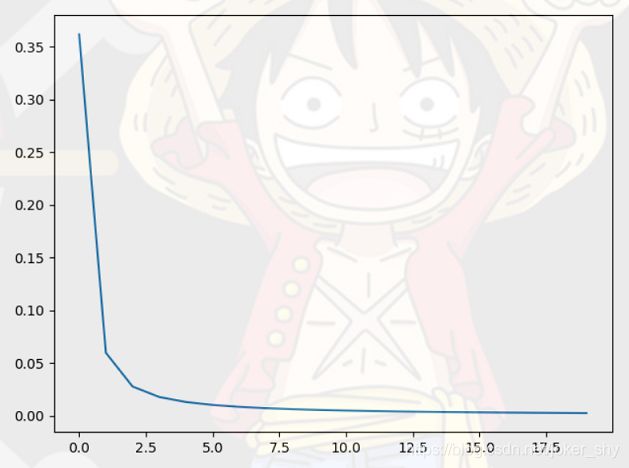
plt.plot(cost_history[1:])
plt.show()
结果如下
Step 0 Cost 0.9873838
Step 500 Cost 0.36180282
Step 1000 Cost 0.059805408
Step 1500 Cost 0.027795581
Step 2000 Cost 0.017842356
Step 2500 Cost 0.013083072
Step 3000 Cost 0.010309634
Step 3500 Cost 0.008498434
Step 4000 Cost 0.00722454
Step 4500 Cost 0.006280598
Step 5000 Cost 0.005553428
Step 5500 Cost 0.0049763597
Step 6000 Cost 0.0045073307
Step 6500 Cost 0.004118765
Step 7000 Cost 0.00379156
Step 7500 Cost 0.0035123003
Step 8000 Cost 0.0032712156
Step 8500 Cost 0.003060991
Step 9000 Cost 0.0028760713
Step 9500 Cost 0.0027121357
Step 10000 Cost 0.002565823
预测值为 [[8.0882706e-04]
[9.9655342e-01]
[9.9778229e-01]
[3.7732117e-03]]