算法--排序算法
JAVA的几种常见排序算法
一:算法类型分析
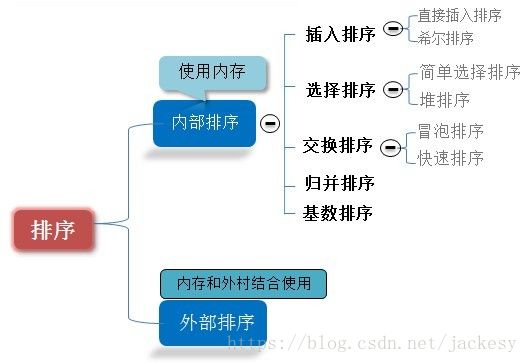
排序算法可以分为内部排序和外部排序。
内部排序是数据记录在内存中进行排序。
外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
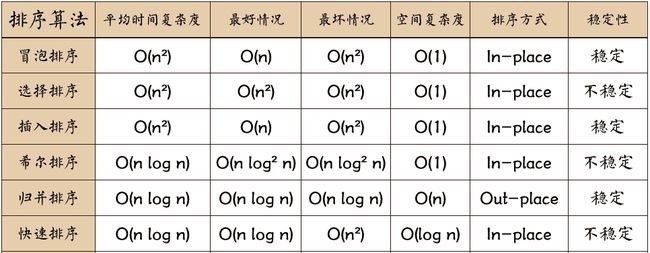
二:几种常见排序算法
1)冒泡排序
a、冒泡排序,是通过每一次遍历获取最大/最小值
b、将最大值/最小值放在尾部/头部
c、然后除开最大值/最小值,剩下的数据在进行遍历获取最大/最小值
d、代码实现
public static void main(String[] args) {
int arr[] = {8, 5, 3, 2, 4};
//冒泡
for (int i = 0; i < arr.length; i++) {
//外层循环,遍历次数
for (int j = 0; j < arr.length - i - 1; j++) {
//内层循环,升序(如果前一个值比后一个值大,则交换)
//内层循环一次,获取一个最大值
if (arr[j] > arr[j + 1]) {
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
}
2)选择排序
a、将第一个值看成最小值
b、然后和后续的比较找出最小值和下标
c、交换本次遍历的起始值和最小值
d、说明:每次遍历的时候,将前面找出的最小值,看成一个有序的列表,后面的看成无序的列表,然后每次遍历无序列表找出最小值。
e、代码实现
public static void main(String[] args) {
int arr[] = {6, 5, 3, 2, 4};
//选择
for (int i = 0; i < arr.length; i++) {
//默认第一个是最小的。
int min = arr[i];
//记录最小的下标
int index = i;
//通过与后面的数据进行比较得出,最小值和下标
for (int j = i + 1; j < arr.length; j++) {
if (min > arr[j]) {
min = arr[j];
index = j;
}
}
//然后将最小值与本次循环的,开始值交换
int temp = arr[i];
arr[i] = min;
arr[index] = temp;
//说明:将i前面的数据看成一个排好的队列,i后面的看成一个无序队列。每次只需要找无需的最小值,做替换
}
}
3)插入排序
a、默认从第二个数据开始比较。
b、如果第二个数据比第一个小,则交换。然后在用第三个数据比较,如果比前面小,则插入(交换)。否则,退出循环
c、说明:默认将第一数据看成有序列表,后面无序的列表循环每一个数据,如果比前面的数据小则插入(交换)。否则退出。
d、代码实现
public static void main(String[] args) {
int arr[] = {7, 5, 3, 2, 4};
//插入排序
for (int i = 1; i < arr.length; i++) {
//外层循环,从第二个开始比较
for (int j = i; j > 0; j--) {
//内存循环,与前面排好序的数据比较,如果后面的数据小于前面的则交换
if (arr[j] < arr[j - 1]) {
int temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
} else {
//如果不小于,说明插入完毕,退出内层循环
break;
}
}
}
}
4)希尔排序(插入排序变种版)
a、基本上和插入排序一样的道理
b、不一样的地方在于,每次循环的步长,通过减半的方式来实现
c、说明:基本原理和插入排序类似,不一样的地方在于。通过间隔多个数据来进行插入排序。
d、代码实现
public static void shellSort(int[] array) {
int number = array.length / 2;
int i;
int j;
int temp;
while (number >= 1) {
for (i = number; i < array.length; i++) {
temp = array[i];
j = i - number;
while (j >= 0 && array[j] < temp) {
array[j + number] = array[j];
j = j - number;
}
array[j + number] = temp;
}
number = number / 2;
}
}
5)快速排序
①. i = L; j = R; 将第一个数设置为key。
②.j--,由后向前找比key小的数。
③.i++,由前向后找比key大的数。
④.i,j相遇交换key和当前值,重复操作
public void quicksort(int[] arr,int left,int right){
if(arr.length == 0) return;
if(left > right) return;
int key = arr[left];
int l = left;
int r = right;
while(l!=r){
//顺序很重要 先从右边找
while(arr[r]>=key && l<r) r--;
//在找左边
while(arr[l]<=key && l<r) l++;
if(l<r){
int temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
}
}
arr[left] = arr[l];
arr[l] = key;
quicksort(arr,left,r-1);
quicksort(arr,l+1,right);
}
6)归并排序
基本思想:
可以将 A,B 组各自再分成二组。依次类推,当分出来的小组只有一个数据时,可以认为这个小组组内已经达到了有序,然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列,再合并数列就完成了归并排序。
//第一个步骤,拆分数组
void mergesort(int a[], int first, int last, int temp[])
{
if (first < last)
{
int mid = (first + last) / 2;
mergesort(a, first, mid, temp); //左边有序
mergesort(a, mid + 1, last, temp); //右边有序
mergearray(a, first, mid, last, temp); //再将二个有序数列合并
}
}
//第二个步骤,归并序列
//将有二个有序数列a[first...mid]和a[mid...last]合并。
void mergearray(int a[], int first, int mid, int last, int temp[])
{
int i = first, j = mid + 1;
int m = mid, n = last;
int k = 0;
while (i <= m && j <= n)
{
if (a[i] <= a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while (i <= m)
temp[k++] = a[i++];
while (j <= n)
temp[k++] = a[j++];
//第三个步骤 额外空间覆盖原始空间
for (i = 0; i < k; i++)
a[first + i] = temp[i];
}
7)堆排序
-
基本思想:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
/** * 构建大顶堆 */ public static void adjustHeap(int[] a, int i, int len) { int temp, j; temp = a[i]; for (j = 2 * i; j < len; j *= 2) {// 沿关键字较大的孩子结点向下筛选 if (j < len && a[j] < a[j + 1]) ++j; // j为关键字中较大记录的下标 if (temp >= a[j]) break; a[i] = a[j]; i = j; } a[i] = temp; } public static void heapSort(int[] a) { int i; for (i = a.length / 2 - 1; i >= 0; i--) {// 构建一个大顶堆 adjustHeap(a, i, a.length - 1); } for (i = a.length - 1; i >= 0; i--) {// 将堆顶记录和当前未经排序子序列的最后一个记录交换 int temp = a[0]; a[0] = a[i]; a[i] = temp; adjustHeap(a, 0, i - 1);// 将a中前i-1个记录重新调整为大顶堆 } }
三:力扣题目解析
215. 数组中的第K个最大元素(中等)
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
1)思想:快速选择
快速选择一般用于求解 k-th Element 问题,可以在 O(n) 时间复杂度,O(1) 空间复杂度完成求解工作。
快速选择的实现和快速排序相似,不过**只需要找到第 k 大的枢(pivot)**即可,不需要对其左右再进行排序。与快速排序一样,快速选择一般需要先打乱数组,否则最坏情况下时间复杂度为 O(n^2)。
**注意:**随机化切分元素。快速排序虽然快,但是在遇到特殊测试用例(顺序数组或者逆序数组)的时候,递归树会退化成链表,时间复杂度会变成 O(N^2)。为了应对极端测试用例,使得递归树加深,可以在循环一开始的时候,随机交换第 1 个元素与它后面的任意 1 个元素的位置;
2)代码实现
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Random;
public class Solution {
private static Random random = new Random(System.currentTimeMillis());
public int findKthLargest(int[] nums, int k) {
int n = nums.length;
int left = 0;
int right = n -1;
k = n-k;
//第k大即n-k小
while(true){
int index = findKth(nums,left, right);
if(index == k){
return nums[k];
}else if(index<k){
left = index+1;
}else{
right = index-1;
}
}
}
public int findKth(int[] nums,int left, int right){
if (right > left) {
int randomIndex = left + 1 + random.nextInt(right - left);
swap(nums, left, randomIndex);
//随机交换
}
int key = nums[left];
int j = left;
for(int i =left+1;i<=right;i++){
if(nums[i]<nums[left]){
j++;
swap(nums,i,j);
}
}
swap(nums,left,j);
return j;
}
public void swap(int[] nums,int i,int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
347. 前 K 个高频元素
1)思想:堆排序
- topk (前k大)用小根堆,维护堆大小不超过 k 即可。每次压入堆前和堆顶元素比较,如果比堆顶元素还小,直接扔掉,否则压入堆。检查堆大小是否超过 k,如果超过,弹出堆顶。复杂度是 nlogk
- 避免使用大根堆,因为你得把所有元素压入堆,复杂度是 nlogn,而且还浪费内存。如果是海量元素,那就挂了。
2)思考
1.为什么不用快排呢?
使用快排要将map转换为vector的结构,然后对整个数组进行排序, 而这种场景下,我们其实只需要维护k个有序的序列就可以了,所以使用优先级队列是最优的
3)代码实现
class Solution {
public int[] topKFrequent(int[] nums, int k) {
int[] result = new int[k];
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
Set<Map.Entry<Integer,Integer>> entries = map.entrySet();
PriorityQueue<Map.Entry<Integer,Integer>> queue = new PriorityQueue<>((o1,o2)->o1.getValue()-o2.getValue());
for(Map.Entry<Integer,Integer> entry : entries){
queue.offer(entry);
if(queue.size()>k){
queue.poll();
}
}
for(int i = k-1;i>=0;i--){
result[i] = queue.poll().getKey();
}
return result;
}
}
451. 根据字符出现频率排序
给定一个字符串,请将字符串里的字符按照出现的频率降序排列。
示例 1:
输入:
"tree"
输出:
"eert"
解释:
'e'出现两次,'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外,"eetr"也是一个有效的答案。
1)思想:堆排序、数组
利用 ASCII 字符集共 128 位,预先建立一个大小为 128 的数组 ,将字符出现的次数放入数组中
2)代码实现
//数组实现
class Solution {
public String frequencySort(String s) {
int[] t = new int[128];
char[] chars = s.toCharArray();
for(char c : chars) {
t[(int)(c)]++;
}
int index = 0;
while(index < s.length()) {
int max = 0;
int cnt = 0;
for(int i = 0; i < 128; i++) {
if(max < t[i]) {
max = t[i];
cnt = i;
}
}
t[cnt] = 0;
while(max-- > 0) {
chars[index++] = (char)(cnt);
}
}
return new String(chars);
}
}
//Map+堆排序
class Solution {
public String frequencySort(String s) {
HashMap<Character,Integer> hash = new HashMap<>();
char[] arr = s.toCharArray();
for(char c:arr){
hash.put(c,hash.getOrDefault(c,0)+1);
}
Set<Map.Entry<Character,Integer>> entries = hash.entrySet();
PriorityQueue<Map.Entry<Character,Integer>> queue = new PriorityQueue<>((o1,o2)->o2.getValue() - o1.getValue());
for(Map.Entry<Character,Integer> entry : entries){
queue.offer(entry);
}
for(int i=0;i<s.length();i++){
char key = queue.peek().getKey();
int k = queue.poll().getValue();
while(k-->0){
arr[i++] = key;
}
}
return String.copyValueOf(arr);
}
}
四:查漏补缺
1)KeySet()和EntrySet()
在Map集合中
values():方法是获取集合中的所有的值----没有键,没有对应关系,
KeySet():
将Map中所有的键存入到set集合中。因为set具备迭代器。所有可以迭代方式取出所有的键,再根据get方法。获取每一个键对应的值。 keySet():迭代后只能通过get()取key
entrySet():
Set
2)完全二叉树
上图,就是一个完全二叉树,其特点在于:
- 从作为第一层的根开始,除了最后一层之外,第N层的元素个数都必须是2的N次方;第一层2个元素,第二层4个,第三层8个,以此类推。
- 而最后一行的元素,都要紧贴在左边,换句话说,每一行的元素都从最左边开始安放,两个元素之间不能有空闲,具备了这两个特点的树,就是一棵完全二叉树。
3)完全二叉树与堆关系
堆是一种非线性结构,可以把堆看作一个数组,也可以被看作一个完全二叉树,通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组
4)大顶堆与小顶堆
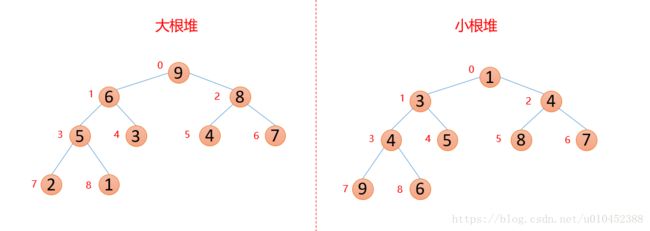
按照堆的特点可以把堆分为大顶堆和小顶堆
大顶堆:每个结点的值都大于或等于其左右孩子结点的值
小顶堆:每个结点的值都小于或等于其左右孩子结点的值
(堆的这种特性非常的有用,堆常常被当做优先队列使用,因为可以快速的访问到“最重要”的元素)
如上图,左边就是大根堆;右边则是小根堆,这里必须要注意一点,只要求子节点与父节点的关系,两个节点的大小关系与其左右位置没有任何关系。
我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
我们用简单的公式来描述一下堆的定义就是:(读者可以对照上图的数组来理解下面两个公式)
**大顶堆:**arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
**小顶堆:**arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
还有一个基本概念:查找数组中某个数的父结点和左右孩子结点,比如已知索引为i.父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
1.父结点索引:(i*-1)/2(这里计算机中的除以2,省略掉小数)
2.左孩子索引:2*i+1
3.右孩子索引:2*i+2
5)Comparator
在comparator里面,-1代表小于,0代表等于,1代表大于
o1代表前一个元素,o2代表后一个元素
6)数组和字符串的转换
1) 存在错误
直接使用arr.toString 得到的是一个地址,而不是字符串
2)正确方法
1.字符数组转成字符串
//(1)直接在构造String时转换
char[] array = new char[]{'a','b','c','d','e','f','g'};
String str = new String(array);
//(2)调用String类的提供的方法的valueOf()
String str2 = String.valueOf(array);
小顶堆:**arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
还有一个基本概念:查找数组中某个数的父结点和左右孩子结点,比如已知索引为i.父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
1.父结点索引:(i*-1)/2(这里计算机中的除以2,省略掉小数)
2.左孩子索引:2*i+1
3.右孩子索引:2*i+2
5)Comparator
在comparator里面,-1代表小于,0代表等于,1代表大于
o1代表前一个元素,o2代表后一个元素
6)数组和字符串的转换
1) 存在错误
直接使用arr.toString 得到的是一个地址,而不是字符串
2)正确方法
1.字符数组转成字符串
//(1)直接在构造String时转换
char[] array = new char[]{'a','b','c','d','e','f','g'};
String str = new String(array);
//(2)调用String类的提供的方法的valueOf()
String str2 = String.valueOf(array);