灰色预测GM(1,n)模型_python

灰色系统理论及其应用系列博文：
一、灰色关联度分析法(GRA)_python
二、灰色预测模型GM(1,1)

一、GM(1,n)算法

二、示例

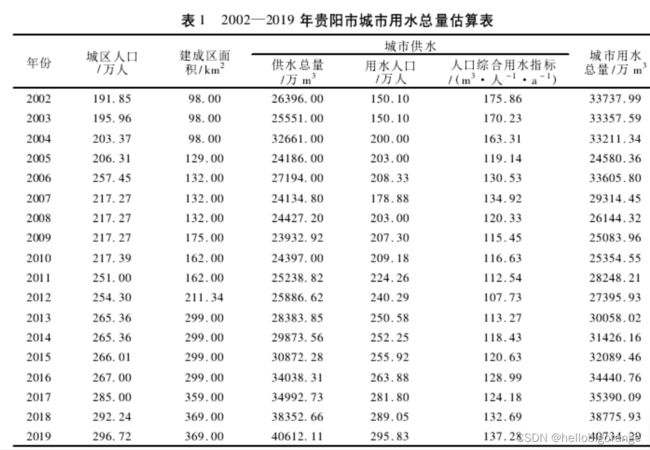
注：数据均来自论文《基于灰色系统理论的贵阳市城市用水总量预测》

2.1 数据：

data.csv
年份,城区人口,建成区面积,供水总量,用水人口,人口综合用水指标,城市用水总量
2002, 191.85, 98.00, 26396.00, 150.10, 175.86, 33737.99
2003, 195.96, 98.00, 25551.00, 150.10, 170.23, 33357.59
2004, 203.37, 98.00, 32661.00, 200.00, 163.31, 33211.34
2005, 206.31, 129.00, 24186.00, 203.00, 119.14, 24580.36
2006, 257.45, 132.00, 27194.00, 208.33, 130.53, 33605.80
2007, 217.27, 132.00, 24134.80, 178.88, 134.92, 29314.45
2008, 217.27, 132.00, 24427.20, 203.00, 120.33, 26144.32
2009, 217.27, 175.00, 23932.92, 207.30, 115.45, 25083.96
2010, 217.39, 162.00, 24397.00, 209.18, 116.63, 25354.55
2011, 251.00, 162.00, 25238.82, 224.26, 112.54, 28248.21
2012, 254.30, 211.34, 25886.62, 240.29, 107.73, 27395.93
2013, 265.36, 299.00, 28383.85, 250.58, 113.27, 30058.02
2014, 265.36, 299.00, 29873.56, 252.25, 118.43, 31426.16
2015, 266.01, 299.00, 30872.28, 255.92, 120.63, 32089.46
2016, 267.00, 299.00, 34038.31, 263.88, 128.99, 34440.76
2017, 285.00, 359.00, 34992.73, 281.80, 124.18, 35390.09
2018, 292.24, 369.00, 38352.66, 289.05, 132.69, 38775.93
2019, 296.72, 369.00, 40612.11, 295.83, 137.28, 40734.29

上面的数据中，最后一列城市用水总量为需要预测的数据列，其他列为相关因素列

2.2 代码_使用GM(1,n)城市用水总量

以 2002—2019 年各年间估算的城市用水总量，运用 GM(1,7) 模型分别得到原始数据序列的响应式。

# -*- coding: utf-8 -*- 
# @Time : 2022/3/18 14:18 
# @Author : Orange
# @File : g_pred.py.py

# -*- coding: utf-8 -*- 
# @Time : 2022/3/18 14:18 
# @Author : Orange
# @File : g_pred.py.py

from decimal import *


class GM11():
    def __init__(self):
        self.f = None

    def isUsable(self, X0):
        '''判断是否通过光滑检验'''
        X1 = X0.cumsum()
        rho = [X0[i] / X1[i - 1] for i in range(1, len(X0))]
        rho_ratio = [rho[i + 1] / rho[i] for i in range(len(rho) - 1)]
        print(rho, rho_ratio)
        flag = True
        for i in range(2, len(rho) - 1):
            if rho[i] > 0.5 or rho[i + 1] / rho[i] >= 1:
                flag = False
        if rho[-1] > 0.5:
            flag = False
        if flag:
            print("数据通过光滑校验")
        else:
            print("该数据未通过光滑校验")

        '''判断是否通过级比检验'''
        lambds = [X0[i - 1] / X0[i] for i in range(1, len(X0))]
        X_min = np.e ** (-2 / (len(X0) + 1))
        X_max = np.e ** (2 / (len(X0) + 1))
        for lambd in lambds:
            if lambd < X_min or lambd > X_max:
                print('该数据未通过级比检验')
                return
        print('该数据通过级比检验')

    def train(self, X0):
        X1 = X0.cumsum(axis=0)  # [x_2^1,x_3^1,...,x_n^1,x_1^1] # 其中x_i^1为x_i^01次累加后的列向量
        Z = (np.array([-0.5 * (X1[:, -1][k - 1] + X1[:, -1][k]) for k in range(1, len(X1[:, -1]))])).reshape(
            len(X1[:, -1]) - 1, 1)
        # 数据矩阵A、B
        A = (X0[:, -1][1:]).reshape(len(Z), 1)
        B = np.hstack((Z, X1[1:, :-1]))
        # 求参数
        u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(A)
        a = u[0][0]
        b = u[1:]
        print("灰参数a：", a, "，参数矩阵b：", b)
        self.f = lambda k, X1: (X0[0, -1] - (1 / a) * (X1[k, ::]).dot(b)) * np.exp(-a * k) + (1 / a) * (X1[k, ::]).dot(
            b)

    def predict(self, k, X0):
        '''
        :param k: k为预测的第k个值
        :param X0: X0为【k*n】的矩阵,n为特征的个数，k为样本的个数
        :return:
        '''
        X1 = X0.cumsum(axis=0)
        X1_hat = [float(self.f(k, X1)) for k in range(k)]
        X0_hat = np.diff(X1_hat)
        X0_hat = np.hstack((X1_hat[0], X0_hat))
        return X0_hat

    def evaluate(self, X0_hat, X0):
        '''
        根据后验差比及小误差概率判断预测结果
        :param X0_hat: 预测结果
        :return:
        '''
        S1 = np.std(X0, ddof=1)  # 原始数据样本标准差
        S2 = np.std(X0 - X0_hat, ddof=1)  # 残差数据样本标准差
        C = S2 / S1  # 后验差比
        Pe = np.mean(X0 - X0_hat)
        temp = np.abs((X0 - X0_hat - Pe)) < 0.6745 * S1
        p = np.count_nonzero(temp) / len(X0)  # 计算小误差概率
        print("原数据样本标准差：", S1)
        print("残差样本标准差：", S2)
        print("后验差：", C)
        print("小误差概率p：", p)


if __name__ == '__main__':
    import matplotlib.pyplot as plt
    import numpy as np
    import pandas as pd

    plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
    plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）
    data = pd.read_csv("data.csv")
    # data.drop('供水总量', axis=1, inplace=True)
    # 原始数据X
    X = data.values
    # 训练集
    X_train = X[:, :]
    # 测试集
    X_test = []

    model = GM11()
    model.isUsable(X_train[:, -1])  # 判断模型可行性
    model.train(X_train)  # 训练
    Y_pred = model.predict(len(X), X[:, :-1])  # 预测
    Y_train_pred = Y_pred[:len(X_train)]
    Y_test_pred = Y_pred[len(X_train):]
    score_tRAIN = model.evaluate(Y_train_pred, X_train[:, -1])  # 评估
    # score_test = model.evaluate(Y_test_pred, X_test[:, -1])

    # 可视化
    plt.grid()
    plt.plot(np.arange(len(Y_train_pred)), X_train[:, -1], '->')
    plt.plot(np.arange(len(Y_train_pred)), Y_train_pred, '-o')
    plt.legend(['负荷实际值', '灰色预测模型预测值'])
    plt.title('训练集')
    plt.show()

    # # 可视化
    # plt.grid()
    # plt.plot(np.arange(len(Y_test_pred)), X_test[:, -1], '->')
    # plt.plot(np.arange(len(Y_test_pred)), Y_test_pred, '-o')
    # plt.legend(['负荷实际值', '灰色预测模型预测值'])
    # plt.title('测试集')
    # plt.show()

2.3 结果分析

以贵阳市 2002—2019 年各年间城市用水总量计算灰色预测模型，得到各关键参数如下:
1). 一阶累加X1：

2). 邻近均值生成序列Z:
z=[[ -50416.785], [ -83701.25 ], [-112597.1 ], [-141690.18 ], [-173150.305], [-200879.69 ], [-226493.83 ], [-251713.085], [-278514.465], [-306336.535], [-335063.51 ], [-365805.6 ], [-397563.41 ], [-430828.52 ], [-465743.945], [-502826.955], [-542582.065]]
3). 系数矩阵B

4.) 常量向量A
A=[[33357.59], [33211.34], [24580.36], [33605.8 ], [29314.45], [26144.32], [25083.96], [25354.55], [28248.21], [27395.93], [30058.02], [31426.16], [32089.46], [34440.76], [35390.09], [38775.93], [40734.29]]
5). 计算得灰参数矩阵u
u= [[ 2.10865303], [ -0.79661015], [ 268.27615473], [ 9.50904062], [ 2.04108088], [-289.38654309], [ 50.36476197]]
6). 计算得${\widehat{x_1}}^{(1)}$
${\widehat{x_1}}^{(1)}=[33737.99,62136.41059571255,98714.77263514209,123994.65466594681,157570.90630726953,187108.145194742,213249.99530402914,238397.28249186202,263719.7944647677,291965.5572243266,319165.5173481615,349304.8797308811,380779.8949102532,412852.82970389083,447223.18020760675,482503.4498108375,521210.1028053897,561852.5575612668]$
7). 累减还原得${\widehat{x_1}}^{(0)}$
[33737.99 28398.42059571 36578.36203943 25279.8820308, 33576.25164132 29537.23888747 26141.85010929 25147.28718783, 25322.51197291 28245.76275956 27199.96012383 30139.36238272, 31475.01517937 32072.93479364 34370.35050372 35280.26960323, 38706.65299455 40642.45475588]
8）评估
后验差： 0.315294126575022
小误差概率p： 0.8888888888888888
9) 可视化

在上一篇文章中，用GM(1,1)预测城市用水量，得到c=0.819，p=0.44可以看出本文采取GM(1,N)模型后，效果明显提升。