贝叶斯分类及其代码

        学期末的综述报告我选择了贝叶斯分类，既然已经写了就将它分享一下。 主要目的就是以教促学。   如有问题欢迎在评论区进行讨论。

        随着现代社会信息技术的发展，对于数据的挖掘越来越重要，分类是数据挖掘中应用领域极其广泛的技术之一[1]， 目前应用比较普遍 的几种分类方法中，朴素贝叶斯[2]在处理分类问题上简单 高效，是机器学习和数据挖掘中一个重要的算法。朴素贝叶斯算法是机器学习和数据挖掘中被广泛应 用的一种分类算法[3],，它先基于贝叶斯定理和属性条件独 立性假设来计算待判样本属于各类的条件概率，再将其判别为概率最大的那一类。[4]

基本思想及理论

        与其他绝大部分机器学习分类算法不同，贝叶斯分类器并不是直接学习特征输出类别Y与x之间的关系来进行分类，而是找出输出类别Y与特征之间的联合分布函数P(X,Y)，然后利用贝叶斯公式获得分类的结果。贝叶斯分类是在概率框架下实施决策，在概率已知的理想情况下，利用概率和损失来标识数据类别。其中比较常用的朴素贝叶斯分类器是基于特征条件相互独立的条件下利用贝叶斯公式进行分类。主要步骤为在训练集中基于特征相互独立的条件输出联合概率分布；在此基础上，对于输入的样本x，输出后验概率较大的类别y。

        在通常的模式识别问题中，我们的目标都是事错误率最小化。利用概率论的贝叶斯公式，可以获得使错误率最小的分类决策，即最小错误率贝叶斯决策。概率中贝叶斯公式为

是先验概率；是x与的联合概率密度；为总体密度；是类条件密度。贝叶斯决策是在类条件概率密度和先验概率已知的情况下，通过贝叶斯公式计算后验概率，以后验概率最大的类别为样本的类别。朴素贝叶斯分类是通过计算条件概率实现分类预测，条件概率计算的理论依据是贝叶斯定理[5]。

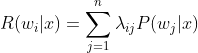样本有n种类型标记，即，是将真误分类为所造成的损失，利用后验概率可以求得样本x分成的期望损失，即条件风险，对于整个数据样本集，样本集总风险，也就是条件风险的期望。分类器的目的是最小化样本数据集的总体风险，倘若每一个样本的条件风险都最小，那么总体风险也就会最小。这也就是贝叶斯判定准则：在每一个样本上都以条件风险最小的类型为类型标定，即。在实际的数据集中，需要从中获得样本x的先验概率和后验概率。先验概率依据大数定律直接通过训练集的频率计算出来，后验概率则需要通过极大似然估计来获得。

 

朴素贝叶斯分类器

朴素贝叶斯分类器基于“属性条件相互独立的”假设上。基于贝叶斯公式来判定样本属性需要求取先验概率和类条件概率。先验概率可以通过大数定理转化为频率，表示为，表示为训练集D中第w类样本的集合。

对于后验概率常用策略是假设数据集服从一定的概率分布，在训练集上利用已知样本对参数进行估计。假设具是被参数唯一确定的形式，可以利用训练集D估计参数.基于朴素贝叶斯分类所有样本独立同分布的假设，利用极大似然估计可以获得，使用对数似然，此时参数的极大似然估计就为.在实际分类器中，离散数据的后验概率为，其中表示第i个属性上取值为的集合大小。如果是连续性的数据的话，则考虑其服从正态分布，代表第w类样本在第i个属性上的均值，代表方差，也就是。

朴素贝叶斯算法流程

1、确定分类的类型和特征属性，量化所有的特征属性，将总样本按照一定的比例分成训练集和验证集。假设此时训练集由m个样本，n个特征属性，一共可以分为k个类别，每个类别的样本数量为类别标记为w。

2、计算此时k个类别的先验概率:

3、计算第k个类别的第j个特征的第i个取值的条件概率，一般情况下建立概率密度函数，认为后验概率服从正态分布，即，求解出方差和均值。

4、对于测试集中的样本x，分别计算其在各个类别中的概率即

5、在计算完样本x所有类别的概率后，选择概率最大的类别作为样本的类别特征。

贝叶斯分类器的python代码实现

基于贝叶斯算法的流程，可以编写出相应的代码。分为三个基本部分，计算类型的先验概率，和对应的条件概率、方差、均值；获取测试样本的条件概率，计算后验概率；将测试样本概率可能性最大的类别作为判断的类型。具体代码已经放在附录了。

参考文献

[1]刘红岩,陈剑,陈国青.数据挖掘中的数据分类算法综述[J].清华大 学学报(自然科学版),2002,(6).

[2]郭勋诚.朴素贝叶斯分类算法应用研究[J].通讯世界,2019,26(1)

[3]李琼阳,田萍.基于主成分分析的朴素贝叶斯算法在垃圾短信用户 识别中的应用[J].数学的实践与认识,2019,49(1)

[4]基于改进PCA的朴素贝叶斯分类算法 李思奇; 吕王勇; 邓柙; 陈雯 统计与决策 [J] 2021-12-06

[5]毛国君，段立娟．数据挖掘原理与算法［M］．北京: 清华大学出版社，2015: 138－139．

[6]https://blog.csdn.net/qq_38163244/article/details/109144003

[7]https://blog.csdn.net/a16111597162163/article/details/101646332

#代码来自​https://blog.csdn.net/a16111597162163/article/details/101646332​，我将其调整使其可以正常运行。
import numpy as np
import pandas as pd
class NaiveBayes():
 
    def __init__(self):
 
        self._X_train = None
        self._y_train = None
        self._classes = None
        self._priorlist = None
        self._meanmat = None
        self._varmat = None
 
    def fit(self, X_train, y_train):
        
        self._X_train = X_train
        self._y_train = y_train
         #  得到各个类别
        self._classes = np.unique(self._y_train)                      
        priorlist = []
        #生成与样本特征数相同的零矩阵
        meanmat0 = np.zeros((1,self._X_train.shape[1]))      
        varmat0 = np.zeros((1,self._X_train.shape[1]))
        for i, c in enumerate(self._classes):
            # 计算每个种类的平均值，方差，先验概率
            # 属于某个类别的样本组成的“矩阵”
            X_Index_c = self._X_train[np.where(self._y_train == c)] 
             # 计算类别的先验概率
            priorlist.append(X_Index_c.shape[0] / self._X_train.shape[0]) 
             # 计算该类别下每个特征的均值，结果保持二维状态[[3 4 6 2 1]]
            X_index_c_mean = np.mean(X_Index_c, axis=0, keepdims=True) 
            # 方差
            X_index_c_var = np.var(X_Index_c, axis=0, keepdims=True)
            # 各个类别下的特征均值矩阵罗成新的矩阵，每行代表一个类别。
            meanmat0 = np.append(meanmat0, X_index_c_mean, axis=0)         
            varmat0 = np.append(varmat0, X_index_c_var, axis=0)
        self._priorlist = priorlist
         #除去开始多余的第一行
        self._meanmat = meanmat0[1:, :]                                   
        self._varmat = varmat0[1:, :]
 
    def predict(self,X_test):
        # 防止分母为0
        eps = 1e-10
         #用于存放测试集中各个实例的所属类别
        classof_X_test = []                                               
        for x_sample in X_test:
            #将每个实例沿列拉长，行数为样本的类别数
            matx_sample = np.tile(x_sample,(len(self._classes),1))         
            mat_numerator = np.exp(-(matx_sample - self._meanmat) ** 2 / (2 * self._varmat + eps))
            mat_denominator = np.sqrt(2 * np.pi * self._varmat + eps)
            # 每个类别下的类条件概率取对数后相加
            list_log = np.sum(np.log(mat_numerator/mat_denominator),axis=1)
            # 加上类先验概率的对数
            prior_class_x = list_log + np.log(self._priorlist)             
            # 取对数概率最大的索引
            prior_class_x_index = np.argmax(prior_class_x)     
            # 返回一个实例对应的类别
            classof_x = self._classes[prior_class_x_index]                 
            classof_X_test.append(classof_x)
        return classof_X_test
 
    def score(self, X_test, y_test):
        
        j = 0
        for i in range(len(self.predict(X_test))):
            if self.predict(X_test)[i] == y_test[i]:
                j += 1
        return ('accuracy: {:.10%}'.format(j / len(y_test)))
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split,cross_val_score
dataSet=load_breast_cancer()

data=dataSet.data#获取数据集
label=dataSet.target#标签
x_train,x_test,y_train,y_test=train_test_split(data,label,test_size=0.2)
forcast = NaiveBayes()
forcast.fit(x_train,y_train)
print(forcast.predict(x_test))
print(forcast.score(x_test,y_test))

from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf.fit(x_train,y_train)
clf.predict(x_test)
clf.score(x_test,y_test)