机器学习多元线性回归模型(公式推导以及代码实现)
一、理论部分
二、代码实现
三、感想
一、理论部分(公式推导)
1.1、线性回归
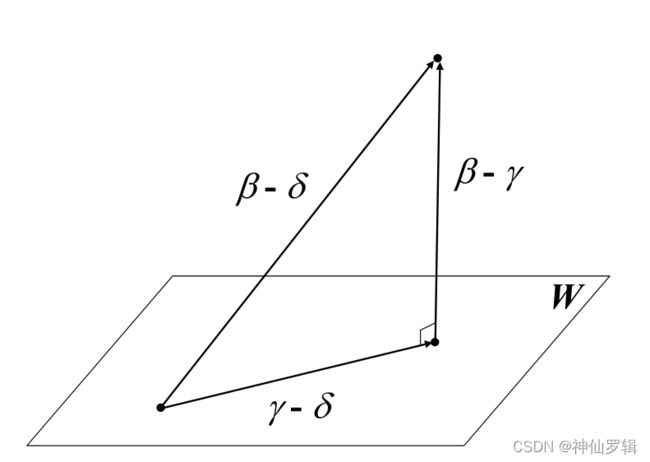
矩阵最小二乘法(参考高等代数)
这部分知识可以参考:
高等代数9 7 向量到子空间的距离 最小二乘法 - 道客巴巴![]() https://www.doc88.com/p-873117402915.html
https://www.doc88.com/p-873117402915.html
![]()
求C = y-Y 最小值--> C = y-XA (b = b![]() )
)
![]() ,
,![]() ,...,
,...,![]() ,y 通过已知数据获得。
,y 通过已知数据获得。
在向量空间L(![]() ,
,![]() ,...,
,...,![]() )C垂直于 L(
)C垂直于 L(![]() ,
,![]() ,...,
,...,![]() )
)
只需且必须(C,![]() ) = (C,
) = (C,![]() )=......=(C,
)=......=(C,![]() )= (C,
)= (C,![]() ) = 0
) = 0
联立方程求解就行了。详情请参考链接,里面有例题。(公式在博客里太难编辑了)
这里需要注意的是 A*A必须满秩。如果不满秩,方程组的解是一个基础解系,无穷多个解。
什么时候会出现这种情况:如 训练集只有3组,而给的特征就有4个,这样上述求的解是无穷个的。(把矩阵化成上三角矩阵就可以看出)
1.2、非线性回归
二、代码实现
2.1、手写代码。(可直接运行)
2.2、代码解释。
def fit(self, numpy_data, numpy_result):
np_ones = np.ones((len(numpy_data), 1))
numpy_data = np.c_[numpy_data, np_ones]
data_transpose = numpy_data.transpose()
A = np.matmul(data_transpose, numpy_data)
b = np.matmul(data_transpose, numpy_result)
self.result = np.linalg.solve(A, b)了解公式原理,代码就简单了。
1、创建全为1 numpy类型,添加到数据里。把y = kx+b 中的b看作b乘以全为1的向量
2、求矩阵的转置,transpose()
3、np.linalg.solve()联立方程组求解。
def predict(self, data):
numpy_result = np.zeros(len(data))
for index, datas in enumerate(data):
numpy_result[index] = np.sum(
[data * self.result[index] for index, data in enumerate(datas)])
+ self.result[-1]
return numpy_result这部分是预测,输入一个新的样本数据,我们通过建立的模型进行预测。
data1 = np.array([[3.6, 3.7, 3.8, 3.9]])
data2 = np.array([[i for i in range(1, 5)]])
result_tranpose = np.array([[1.0, 0.9, 0.85, 0.81]])
original_transpose = np.concatenate((data1, data2))
data_original = original_transpose.transpose()
data_result = result_tranpose.transpose()
print(data_original)
print(data_result)
[[3.6 1. ]
[3.7 2. ]
[3.8 3. ]
[3.9 4. ]]
[[1. ]
[0.9 ]
[0.85]
[0.81]]我们构造一些数据来进行验证。
# 建模
linear = LinearModel()
linear.fit(data_original, data_result)
print(linear.result) # 计算的系数值
# 预测
predict = linear.predict([[3.6, 1], [3.7, 2]])
print(predict)
[[ 0.24109375]
[-0.08610938]
[ 0.20117188]]
[0.983 0.921]2.3、完整代码。
import numpy as np
class LinearModel():
def __init__(self):
super(LinearModel, self).__init__()
def fit(self, numpy_data, numpy_result):
np_ones = np.ones((len(numpy_data), 1))
numpy_data = np.c_[numpy_data, np_ones]
data_transpose = numpy_data.transpose()
A = np.matmul(data_transpose, numpy_data)
b = np.matmul(data_transpose, numpy_result)
self.result = np.linalg.solve(A, b)
def predict(self, data):
numpy_result = np.zeros(len(data))
for index, datas in enumerate(data):
numpy_result[index] = np.sum(
[data * self.result[index] for index, data in enumerate(datas)]) +
self.result[-1]
return numpy_result
if __name__ == '__main__':
# 数据集准备
data1 = np.array([[3.6, 3.7, 3.8, 3.9]])
data2 = np.array([[i for i in range(1, 5)]])
result_tranpose = np.array([[1.0, 0.9, 0.85, 0.81]])
original_transpose = np.concatenate((data1, data2))
data_original = original_transpose.transpose()
data_result = result_tranpose.transpose()
# print(data_original)
# print(data_result)
# 建模
linear = LinearModel()
linear.fit(data_original, data_result)
print(linear.result) # 计算的系数值
# 预测
predict = linear.predict([[3.6, 1], [3.7, 2]])
print(predict)
实现非线性也比较简单,只需对代码中numpy_result做相应的处理即可。
三、感想
第一次真正意义上写技术博客,说下感想:感谢csdn,基本解决了我所遇到99%的技术难题。也感谢各位大佬们的技术博客,我从中受益匪浅。为了初学者更好的学习,我也贡献一份力量。加油。
(吐槽下,这自带的公式编辑器真难用。小声bb)