量子计算 4 超光速信息传播?密度矩阵与混合态
量子计算 4 密度矩阵与混合态
- 1 纠缠的量子比特
- 2 光速的信息传播?(bushi)
- 3 密度矩阵(Density matrix)与混合态(Mixed state)
-
- 3.1 混合态
- 3.2 密度矩阵
- 3.3 约化密度矩阵(Reduced density matrix)
- 3.4 酉变换与密度矩阵
- 3.5 No-Communication theorem
- 4 密度矩阵的性质
- 5 Bloch shpere
关注我的微信公众号“熙熙学习笔记”可免费阅读全文
今天的内容,将从两个纠缠的量子比特开始,通过讨论是否可以通过纠缠的量子比特来实现信息的光速传播,由此介绍量子比特的密度矩阵、混合态、Bloch Shpere等概念。
1 纠缠的量子比特
今天的故事要从两个纠缠(Entangled)的量子比特说起。在量子计算3中我们看到,如果两个比特的状态不能用张量积的形式写出来的话,就认为这两个比特间发生了纠缠,在量子计算3中,我们学习了Bell Pair,也称Singlet或者EPR Pair,其可用以下的量子电路产生。
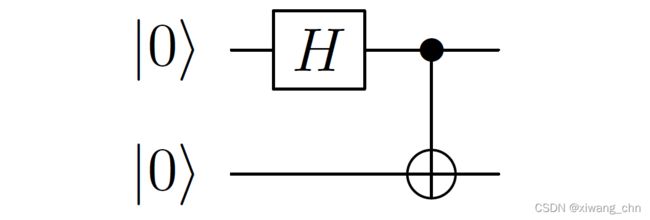
该量子电路的运算如下所示:
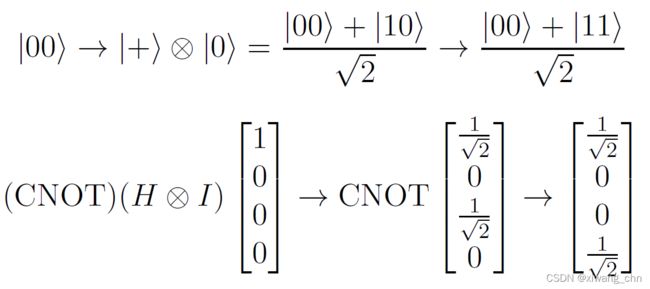
首先用Hadamard门将第一个量子比特从 ∣ 0 ⟩ |0\rangle ∣0⟩变成 ∣ + ⟩ |+\rangle ∣+⟩,然后用CNOT门在第一个量子比特为1的时候翻转第二个量子比特。这样就得到了一个纠缠的Bell Pair。纠缠的量子比特,在纯态的表达方式中,就是双量子比特的纯态无法写成两个独立的量子比特纯态的张量积。
量子纠缠的现象也让爱因斯坦很困惑,因为该现象说明,如果两个量子比特足够接近以至于产生纠缠后,无论将他们分开多远,量子纠缠依然存在。这个最远距离在2018年的时候被中国的卫星试验在150英里也就是240公里的距离上进行了验证。好像两个纠缠的量子比特间有着鬼魅般的联系一样。
2 光速的信息传播?(bushi)
对于该双量子比特状态,Bell Pair = ∣ 00 ⟩ + ∣ 11 ⟩ 2 =\frac{|00\rangle+|11\rangle}{\sqrt{2}} =2∣00⟩+∣11⟩,张三拿着第一个比特跑到了月亮上,李四拿着第二个比特呆在地球,然后张三用基态 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩测量他的量子比特,第一个量子比特会坍塌成 ∣ 0 ⟩ |0\rangle ∣0⟩或者 ∣ 1 ⟩ |1\rangle ∣1⟩,则因为纠缠的作用,李四的量子比特也会坍塌成 ∣ 0 ⟩ |0\rangle ∣0⟩或者 ∣ 1 ⟩ |1\rangle ∣1⟩,这从Bell Pair的状态即可知道。那说明,张三得知自己的结果之后,李四的结果他也马上知道了。这让爱因斯坦很困惑,虽然其他人可能觉得没什么,因为张三并不能控制测量的结果,而两个比特的联系可能就像经典世界里两个随机变量的关联一样。
爱因斯坦进行了更多的脑洞,如果张三在 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩基下测量他的第一个比特呢?那张三要先用H门变换一下然后再用 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩测量,这相当于直接用 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩基测量:
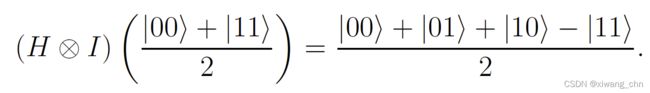
然后张三看到了 ∣ 0 ⟩ |0\rangle ∣0⟩,那李四的量子比特就变成了:
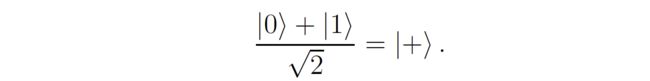
如果张三看到了 ∣ 1 ⟩ |1\rangle ∣1⟩,那李四的量子比特就变成了:
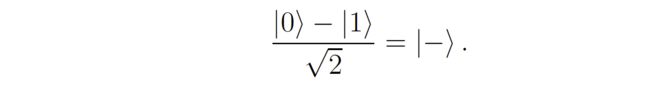
爱因斯坦讨论讲,如果张三用 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩测量,李四的状态会坍塌成 ∣ 0 ⟩ |0\rangle ∣0⟩或者 ∣ 1 ⟩ |1\rangle ∣1⟩,如果张三用 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩测量,李四的状态会坍塌成 ∣ + ⟩ |+\rangle ∣+⟩或者 ∣ − ⟩ |-\rangle ∣−⟩,这好像是一种超光速信息传播。
但是呢,其实李四并不知道张三是用什么基测量的,其实如果李四一直用 ∣ 0 ⟩ |0\rangle ∣0⟩或者 ∣ 1 ⟩ |1\rangle ∣1⟩测量,那不管李四用的是 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩还是 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩,那张三看到 ∣ 0 ⟩ |0\rangle ∣0⟩和 ∣ 1 ⟩ |1\rangle ∣1⟩的概率始终是相同的,因此并没有超光速信息传播,还是符合狭义相对论的。
不过呢,我们还是想使用一种新的状态表达方式,使得李四手里的量子态完全不受张三的影响,这就是密度矩阵的表达方式。
3 密度矩阵(Density matrix)与混合态(Mixed state)
我们看到张三在 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩和 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩两组基下测量的时候,李四的量子比特确实是会坍塌成 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩和 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩两组不同的量子态,而且对李四来说,在张三用 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩测量的时候,李四的量子比特的纯态,有一半的可能是 ∣ 0 ⟩ |0\rangle ∣0⟩,另一半的可能是 ∣ 1 ⟩ |1\rangle ∣1⟩。因此我们将引入密度矩阵和混合态来描述这种纯态的概率分布。
3.1 混合态
我们定义混合态为量子态的概率分布,表达为 { p i , ∣ ψ i ⟩ } \{p_i,|\psi_i\rangle\} {pi,∣ψi⟩},则纯态其实可以认为是混合态的特殊情况,即混合态中某个纯态的概率为1的特殊情况。混合态有个tricky的地方是,不同的纯态概率分布,可能产生同样的混合态。
3.2 密度矩阵
混合态的表达,用密度矩阵来实现,对于混合态 { p i , ∣ ψ i ⟩ } \{p_i,|\psi_i\rangle\} {pi,∣ψi⟩},其密度矩阵为:
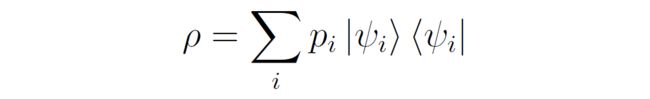
其中 ∣ ψ i ⟩ ⟨ ψ i ∣ |\psi_i\rangle \langle\psi_i| ∣ψi⟩⟨ψi∣是纯态 ∣ ψ i ⟩ |\psi_i\rangle ∣ψi⟩和自己的外积。这使得密度矩阵 ρ \rho ρ是埃尔米特(Hermitian)矩阵。对于标准基 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩态,他们的均匀混合(Mixture)为:
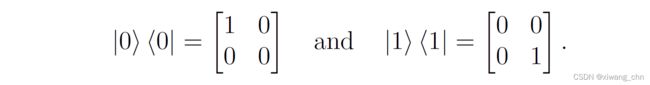
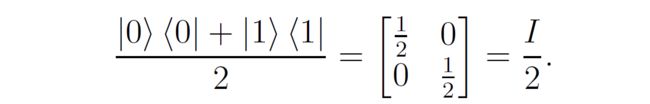
对于Hadamard基 ∣ + ⟩ , ∣ − ⟩ |+\rangle, |-\rangle ∣+⟩,∣−⟩,他们的均匀混合为:
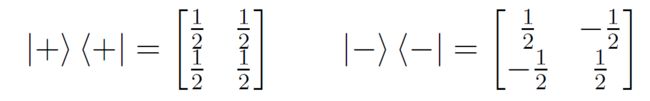
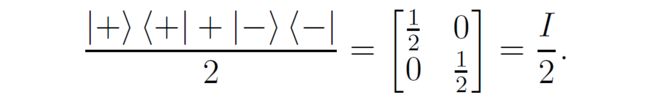
这说明,这两组纯态的均匀混合带来的是相同的密度矩阵,这也对应于不管张三怎么测量,李四的量子比特的量子态都具有同样的密度矩阵。
值得注意的是,对于任意两个正交的基态 ∣ v ⟩ |v\rangle ∣v⟩和 ∣ w ⟩ |w\rangle ∣w⟩,它们的均匀混合都是一样的:
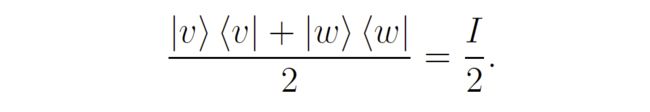
而密度矩阵 I 2 \frac{I}{2} 2I被称为最大混合态(Maximally Mixed State)。可以认为最大混合态就像是一枚均匀的硬币,不管从任意两个正交基 ∣ v ⟩ , ∣ w ⟩ |v\rangle,|w\rangle ∣v⟩,∣w⟩去测量,其结果都是均等的:
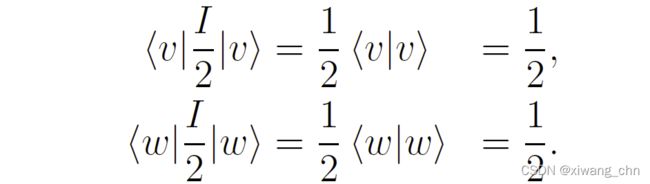
在最大混合态的情况下,张三不管怎么操作和测量,李四的观测结果都不会受到影响。
3.3 约化密度矩阵(Reduced density matrix)
我们讨论的张三李四的这个测量操作过程,可以用另一个方式来打开。我们上面讨论的密度矩阵是对于一个量子比特来讲的,对于另一对纠缠的量子比特来说:
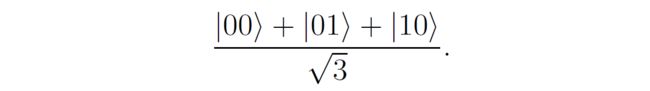
我们怎么找到李四持有的第二个量子比特的密度矩阵呢,首先重写一下,如果张三在 ∣ 0 ⟩ , ∣ 1 ⟩ |0\rangle, |1\rangle ∣0⟩,∣1⟩基下测量的话,重写成以下形式:
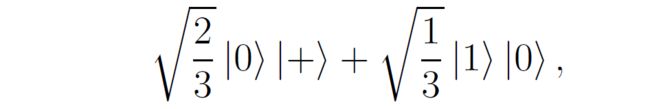
所以张三的测量会有 2 3 \frac{2}{3} 32的概率使得李四的量子比特变成 ∣ + ⟩ |+\rangle ∣+⟩,另有 1 3 \frac{1}{3} 31的概率使得李四的量子比特变成 ∣ 0 ⟩ |0\rangle ∣0⟩。则李四的(约化)密度矩阵为:
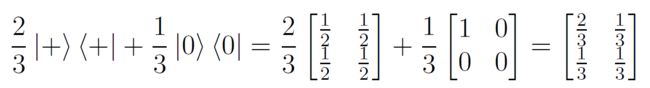
推广一下,对于一个双比特纯态:
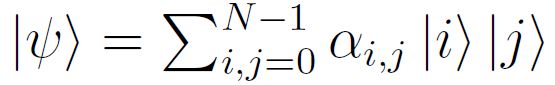
李四的(约化)密度矩阵为:
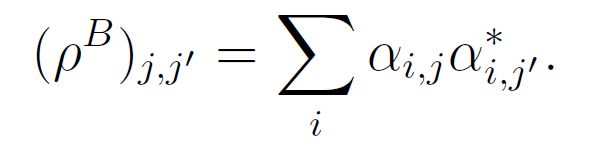
这个从一个复合系统的纯态,到部分系统的混合态的过程,称为 Tracing out.
3.4 酉变换与密度矩阵
对密度矩阵 ρ = ∑ i p i ∣ ψ i ⟩ ⟨ ψ i ∣ \rho=\sum_ip_i |\psi_i\rangle \langle\psi_i| ρ=∑ipi∣ψi⟩⟨ψi∣实施酉变换,相当于:
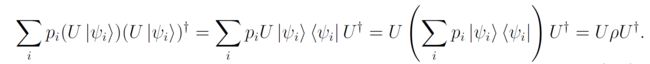
3.5 No-Communication theorem
上述讨论的情况推广一下就是
No-Communication theorem:张三李四共享一个纠缠态,张三的操作都不会影响李四的密度矩阵。
张三观测的结果就可以看成是混合态的概率,对密度矩阵自然没有影响,那张三如果在不同的基下测量,或者使用任意的酉变换,其对李四的密度矩阵也没有影响,这个证明过程可以私信我。
因此量子纠缠也逃不了爱因斯坦的相对论设下的限制,爱因斯坦终于不用纠结超光速传播的问题了。
4 密度矩阵的性质
密度矩阵的非对角项,代表了我们观察到的量子性,在实验中,非对角项越大,说明实验结果越好,而当一个量子系统与环境相互作用时,非对角项会变成零。但是非对角项和基的选择是有关的,通过基变换总可以使得非对角项为零。
密度矩阵计算概率,密度矩阵,里面涵盖了量子比特的所有信息,从3.2 里也看到,对于用密度矩阵表达的混合态,其在基 ∣ v ⟩ |v\rangle ∣v⟩和 ∣ w ⟩ |w\rangle ∣w⟩的测量概率为:
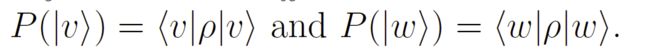
密度矩阵必须是方阵
密度矩阵必须是埃尔米特(Hermitian)矩阵
密度矩阵必须是半正定矩阵,迹为1
因为概率肯定是大于等于零的,且其迹为1,因为概率之和为1。当其秩为1时,表达的就是个纯态。
5 Bloch shpere
当我们将量子比特画在单位圆上时,有一半的空间是浪费的,因为对于量子态 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩和 − ∣ ψ ⟩ -|\psi\rangle −∣ψ⟩,其表达的物理状态相同,因为具有相同的密度矩阵。于是科学家想出来一个好主意,就是把正交的向量画成相反的方向(头大)。
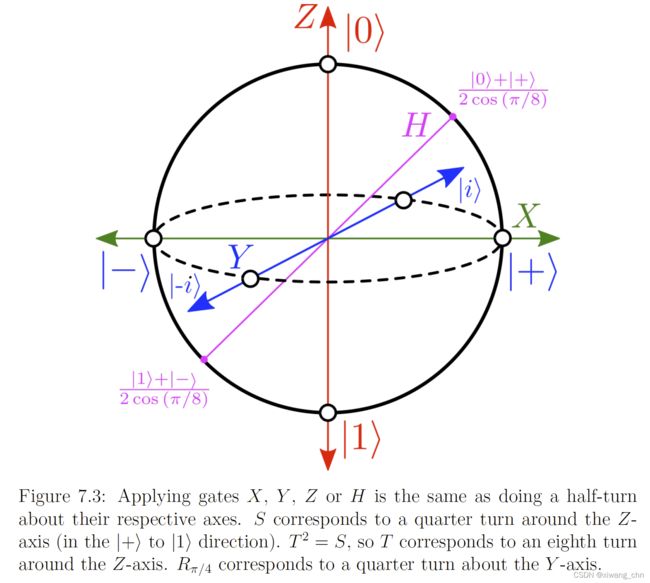
于是, ∣ 0 ⟩ |0\rangle ∣0⟩和 ∣ 1 ⟩ |1\rangle ∣1⟩作为一个轴的两个相反方向,同样的还有 ∣ + ⟩ |+\rangle ∣+⟩和 ∣ − ⟩ |-\rangle ∣−⟩,以及 ∣ i ⟩ |i\rangle ∣i⟩和 ∣ − i ⟩ |-i\rangle ∣−i⟩, ( ∣ i ⟩ = ∣ 0 ⟩ + i ∣ 1 ⟩ 2 , ∣ − i ⟩ = ∣ 0 ⟩ − i ∣ 1 ⟩ 2 ) (|i\rangle=\frac{|0\rangle+i|1\rangle}{\sqrt{2}},|-i\rangle=\frac{|0\rangle-i|1\rangle}{\sqrt{2}}) (∣i⟩=2∣0⟩+i∣1⟩,∣−i⟩=2∣0⟩−i∣1⟩)。于是,一个三维的Bloch Sphere就诞生了!
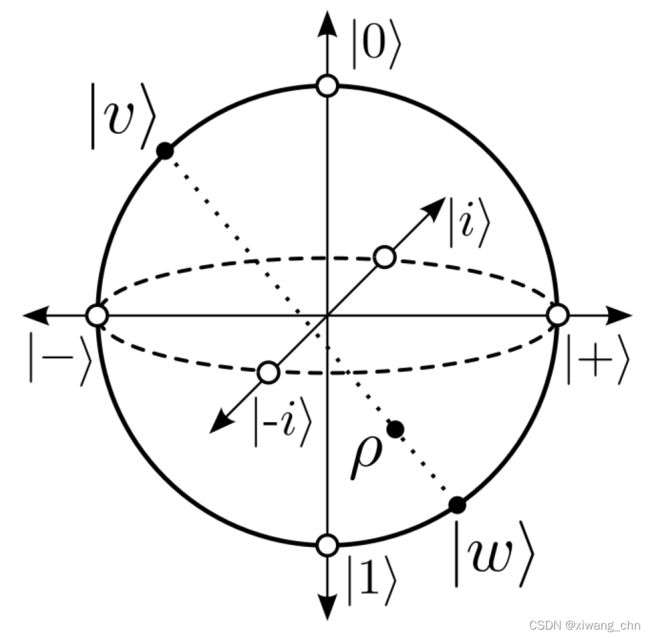
在圆上的状态都是纯态,而里面的点表达的都是混合态,其中原点其实是最大混合态(Maximally mixed state),因为是各种正交基的均匀混合。
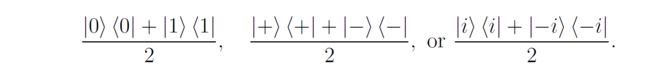
为啥Bloch sphere这么受欢迎还有以一个原因,就是它跟实验很能对得上号,跟电子或其它半自旋粒子的自旋很好的对应起来。原话是“The crazy part here is how the three-dimensionality of the Bloch sphere perfectly syncs up with the three-dimensionality of actual physical space”. https://www.scottaaronson.com/
另外,所有的门操作,都可以看成是Bloch sphere上的某个旋转。
https://www.scottaaronson.com/