稀疏表示 河流多元信息处理 matlab

---

前言

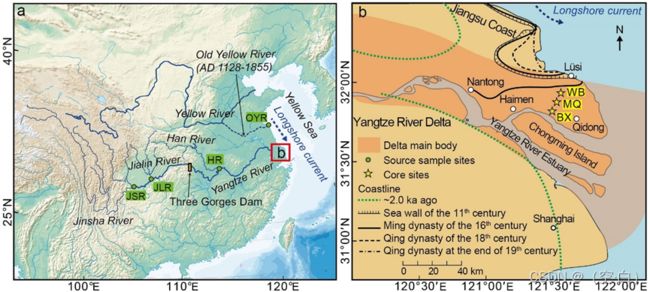
现有来自黄河流域的大量钻孔数据，需要完成以下任务：

1. 简单概括多源数据稀疏表示的基本原理？

2. 如下图，BX、MQ、WB钻孔数据来自于金沙江、嘉陵江、汉江和废黄河四个源头的比重是多少？
   

3. 在题目2的基础上讨论利用PCA给多源数据适当的降维，换句话说就是计算不同个数的元素（Al、Fe、K、Ca、Na、Mg、Ti、Mn、Sr、Ba、V、Cr、Ni、Xlf、Xarm、SIRM、HIRM100、HIRM300、S-100、S-300、Xarm/SIRM）的组成份对钻孔数据来自于金沙江、嘉陵江、汉江和废黄河的比重的影响。

4. 利用高斯核函数方法将EXCEL表中的多源数据进行数据生成使得计算的结果与题2中相似。

具体步骤和结果

一、简要介绍多源数据稀疏表示

1）稀疏表示：

当一个信息号X（可表示为N维列向量的一组向量），可以通过一组N*M的基向量空间，与系数矩阵的乘积表示，如下图.这时候即可用一个M维的列向量映射表示原信号量，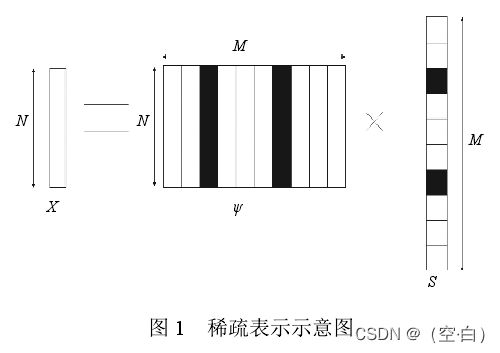
这种情况下，数据量可能变大，也可能变小。但这种情况下基向量空间，与系数矩阵都是自己构造，这就可能出现一种情况，即系数矩阵中非0数据 小于N，此时有效数据（非0）数据小于原数据（N维），成功对数据进行缩减。则这可以称为稀疏表示。

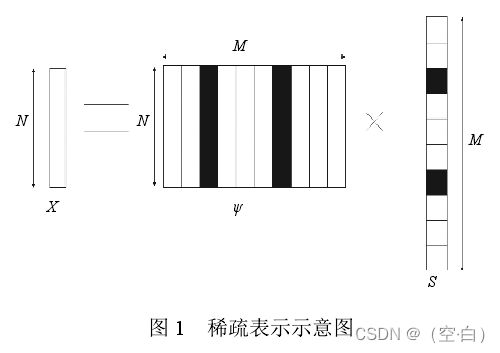
2）稀疏表示在多源信息中的应用：

在上图中，表示了原信息，字典，系数矩阵的关系。在数据处理中，如图像处理中问题中，信息号为原图像，字典是训练的原训练数据，系数矩阵就是信号量来自原训练数据的权重比重。当系数矩阵是稀疏表示（非0数据小于原数据量）。也就是字典（数据集）中有限原子 有效表示的原图像。

二.四个源头的比重

代码：proportion_neo.m
使用稀疏表示的方法

1) 构建字典

取每条金沙江、嘉陵江、汉江和废黄河四个源头的数据作为列向量，构建字典K。每个源头数据有3条，且有21维，所以字典大小为21*12

“A_test = xlsread('./ocean_data_test_16.xlsx');
A_train = xlsread('./ocean_data_train_16.xlsx');
A_test = A_test';
train = A_train';

2）计算系数矩阵

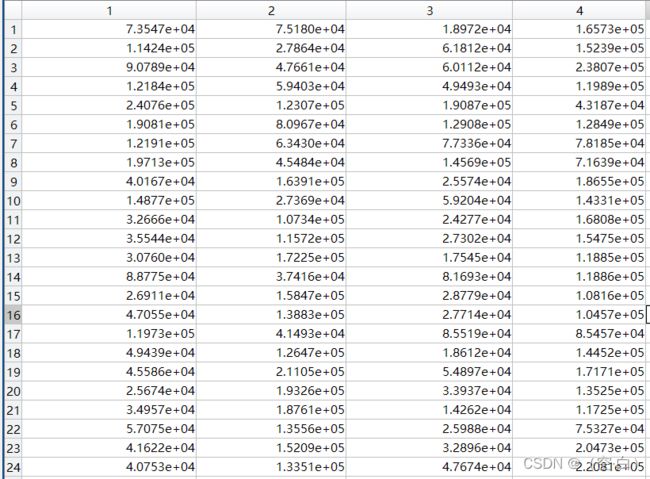
取每条BX、MQ、WB钻孔数据作为原信号，通过线性运算，得到的矩阵系数就是原钻孔数据来自四个源头的比例系数，可以重复多次执行，或者将全部数据作为列向量堆叠成2124的矩阵S，进行矩阵运算。
因为S=KX,X为系数矩阵
则X=K^-1S

SRC_P=train\A_test;
ref=zeros(24,4)

3）加权后的距离

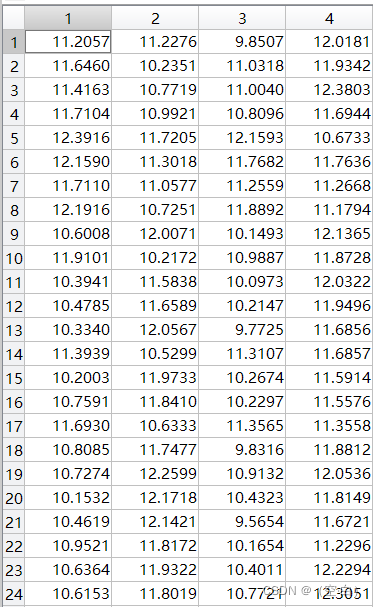
对源头数据（字典）经过系数矩阵加权后，与原数据相减得到距离向量，最后使用欧式距离公式得出距离大小。因为距离大小差异过大，所以对距离数据进行数据处理，通过log函数，使比较大的数据收敛到一定大小如下图二。

	for t = 1:24
    for t1=1:4
        %加权后 字典向量数据
        weighted_train=train(:,3*t1-2:3*t1)*SRC_P(3*t1-2:3*t1,t)
        %数据源与源头的差值
        lenght=A_test(:,t)-weighted_train;
        %欧式距离
        ref(t,t1)=norm(lenght);
    end
	end
	%log函数
	log_ref=log(ref);

4）计算比例

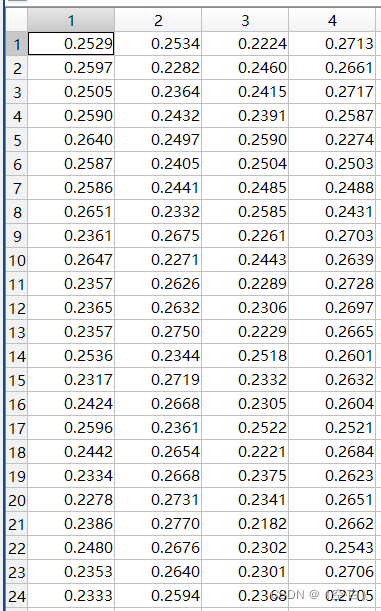
经过处理后得到合适范围的距离数据，由距离数据得到原数据与各源头的距离比重，则通过原数据与各源头距离除以距离之和，如下图

	k=sum(log(ref),2);
	e_ref=log(ref)./k;

三. PCA主成分分析

代码：PCA_neo.m
使用matalb自带PCA分析函数

%合并训练数据和测试数据
total=[A_test;A_train]
%进行主成分分析
[coeff,score,latent,tsquared,explained,mu]=pca(total)

得出的数据中比较重要的是explained和score
explained是主成分贡献度，是我们选取主成分个数的依据

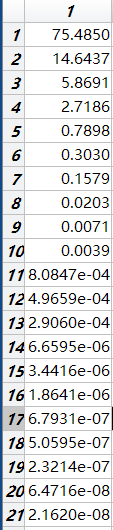
由于前四个主成分已经包含了98%的原数据信息，所以选择将数据降到四维

score是主成分，即样本X在低维空间的投影，也就是我们想要得到的降维后的数据
将提取出来的前四个主成分进行第二步的数据处理，与原21维数据对比

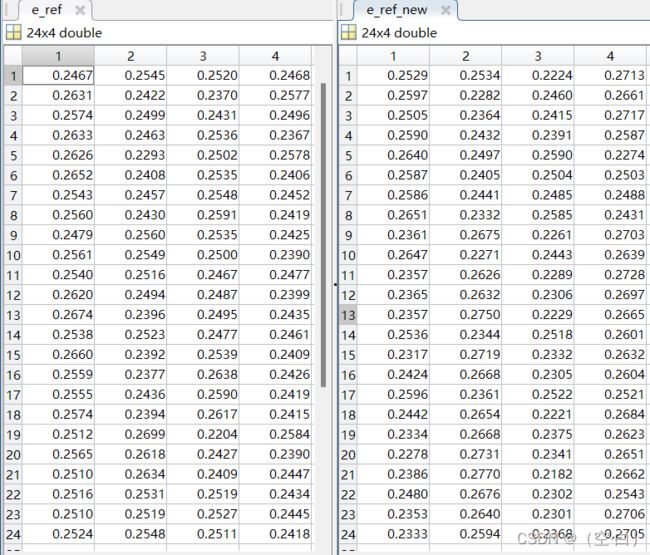
左边为使用前4个主成分得出的源头比例，右边为使用21维向量得出的源头比例

主成分的影响

计算每份数据 使用主主成分分析，与不使用主成分分析的差值，并计算其平均欧式距离。

cha=e_ref_new-e_ref
k=0
for t=cha'
    k=k+norm(t);
end
k=k/24

将平均欧式距离结果作为对比主成分的影响为0.0339。此结果可以认为应该不大，主成分分析在降低数据为4维的情况下，并保持了较高精度的结果。

高斯核函数生成数据

1）目的

高斯核函数生成新的对数据进行升维，以此拓展数据维度，并且保持数据结果与原结果相似。

2）高斯核函数

核心：将有限维数据映射到高维空间，公式如下：

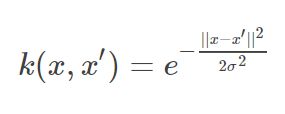
高斯核函数的映射函数如下：

公式中需要确定的值为超参数γ，地标l。地标的个数取决于升维的大小，比如要将原数据的21维升到25维则需要25个地标，这些地标是原特征空间的点。
这里的地标是有样本点得出。理论上，一个特征空间内样本点是无限的，所以可以将每一个样本点映射到一个无穷维的特征空间。但由于真实样本只有36个，所以最多拓展到36维

3)核函数映射运算

代码：gaussian_neo.m
将训练集和测试集合并后，将36个点作为地标,将36个数据映射到36维维的特征空间上，因为数据间差值过大，定义超参数γ为0.000000001，令最后的映射函数的值在合理范围内。

%随机选取36个点，假设全部数据作为地标
ref=zeros(36,36);
%超参数
Y=0.000000001;
for t=1:36
    hang=total(t,:);
   for t1=1:36
       hang-total(t1,:)
       sum(hang-total(t1,:))^2
       exp(-Y*(sum(hang-total(t1,:)))^2)
       ref(t,t1)=exp(-Y*(sum(hang-total(t1,:)))^2);
   end
end
ref
A_test = ref(1:24,:)'
train =ref(25:36,:)'

使用重新映射的36维数据进行目标二的处理，重新得到24个样本来自四个源头的比重的对比数据，如下图。

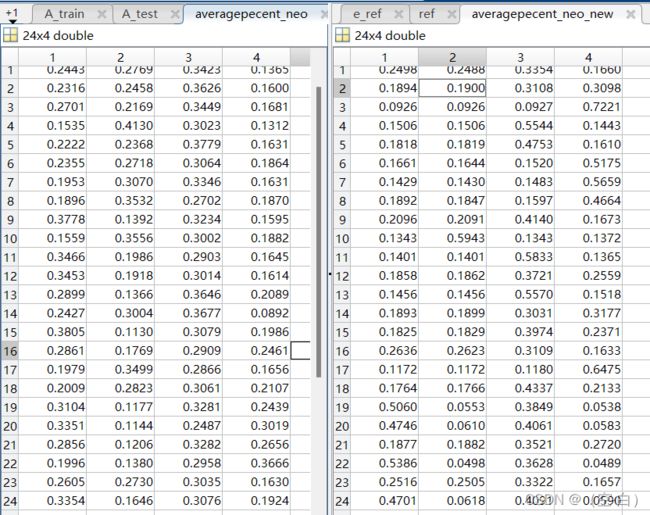
左边为使用前映射的36维样本得出的源头比例，右边为使用21维向量得出的源头比例
计算他们之间的差异值

cha=averagepecent_neo_new-averagepecent_neo
k=0
for t=cha'
    k=k+norm(t);
end
k=k/36

平均每个样本的数据差异达到了0.1862

4）结果分析

每个样本的数据差异达到了0.1862，差异值比较
巨大，可以认为升到高维空间后对源头的比例 与原先相比有巨大差异。原因可能如下

1.核函数的选取：

核函数的映射关系是，映射后的新特征空间的的内积等于核函数的值，这里使用的高斯核函数，所以重新映射的36维相互的内积，即X=K^-1S的运算是符合高斯核的值，高斯核函数如下

即原特征空间与新高维特征空间的关系就是原特征空间的核函数运算等于新高维特征空间样本的乘积。而我们期望更多表示的是在进行线性运算X=K^-1S的时候新特征空间保持不变。使用应该选取线性核。
还有要注意一个点是这时候进行线性运算的是train的广义逆矩阵，所以要进行升维的是train的广义逆矩阵。

二、使用步骤

总结

提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。