二叉树的 前序 中序 后序,面试题小计 根据中序 后序 得出前序
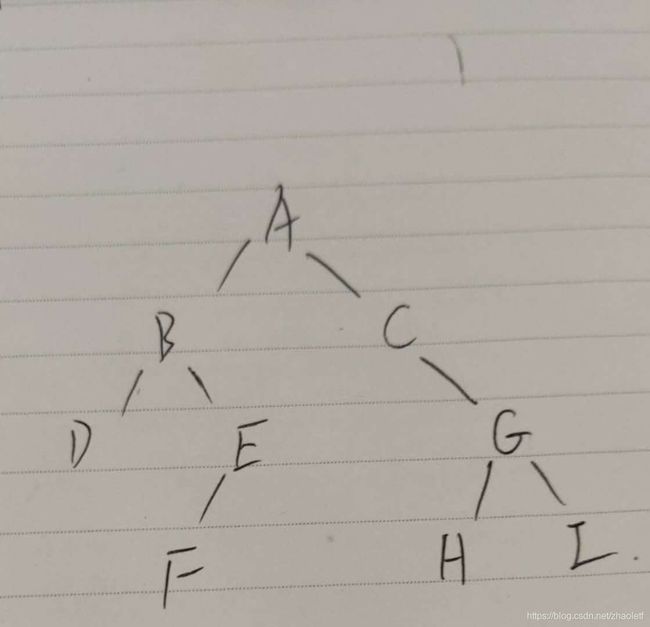
看到一个面试题挺有意思的,记录分享一下.说已知一颗二叉树,如果中序遍历是:DBFEACHGI,后序遍历的节点顺序是:DFEBHIGCA.
可能对二叉树不熟悉的朋友看到这里的时候就蒙了,不知道应该怎么做下去了,其实这个是很简单的,我们只需要记住前序 中序 后序的含义即可:
前序: 根左右;
中序:左根右;
后序:左右根;
不知道朋友们有没有发现一个规律,前序 中序 后序 变化的只是他的根节点,而他的左右子节点的顺序 一直是 从左到右排序的.所以我们只需要记住他根节点的位置即可.下面是一直我在网上找的二叉树的图片:
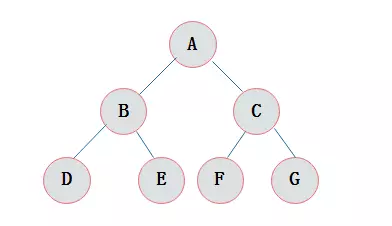
我们可以先用这个图练习一下我们前中后序的一个数据结构.首先前序是: 根左右, 我们可以先找出他的根节点 :A B C;
然后BC呢还有他的子节点,然后我们就可以根据规则:根左右 的顺序把他的子节点添加进去: A + DBE + FCG = ADBEFCG; 所以他的前序就是: ADBEFCG;
同样的道理 中序是:左根右; 就可以先得出 B A C,然后我们在把B
C的子节点也给添加进去: DBE + A + FCG = DBEAFCG;所以他的中序就是:DBEAFCG ;
然后在看他的后序:左右根, 首先我们可以首先得出: B C A,然后在把BC的子节点加进去:DEB + FGC + A=DEBFGCA,所以他的后序就是DEBFGCA.
这个时候我们就可以得出上面二叉图的前序 中序 后序 的数据了.
这个时候在来看我们的面试题:
说已知一颗二叉树,如果中序遍历是:DBFEACHGI,后序遍历的节点顺序是:DFEBHIGCA.
然后通过中序:左根右与后序的:左右根,就可以先确定根节点是 A,
所以DBFE是根节点A的左侧树,
CHGI是根节点A的右侧树.
而他的左右树都是4位,由此推断左右两边的树不是二叉满树
这个时候我们在看他的后序DFEBHIGCA,然后我们在根据后序的公式:左右根,进行嵌套
后序:左右根
DFEB是根节点A的左侧树
HIGC是根节点A的右侧树.
就可以得出 B 是左侧树的根, C 是右侧树的根节点,
中序:左根右
DBFE是根节点A的左侧树,
CHGI是根节点A的右侧树.
通过后序得到左侧树的根节点是 B ,而上面我们也通过中序得到了左右树不是满树.
这个时候我们可以根据中序的左根右进行嵌套左侧树.
B 是根节点,D 是 B 的左侧树,而左侧树是4位,不是一个满二叉树,所以F 与E有一个是根节点,一个是子节点. 而根据 左根右 的定律,E是F的根节点,
同理在看我们的右侧树的根节点是 C ,而 C 的左边没有值,也就是说根节点 C 下面只有一个右侧树,而没有左侧树,这样就可以得出 G 是 C 的右侧树H I 分别是G的左右树.
然后根据这个二叉图,我们就可以得出他的前序:
前序:ABDEFCGHI
中序: DBFEACHGI,
后序:DFEBHIGCA.
朋友们是不是很简单?我们只需要记住二叉树的前中后序变化的只是他的根节点,而他的左右节点的顺序是不变的,这样我们就可以轻松的算出二叉树的顺序了.
如果有不对的地方,请在留言区留言,我会立马修正,如果感觉可以,请点一个赞,方便我也向大家学习.