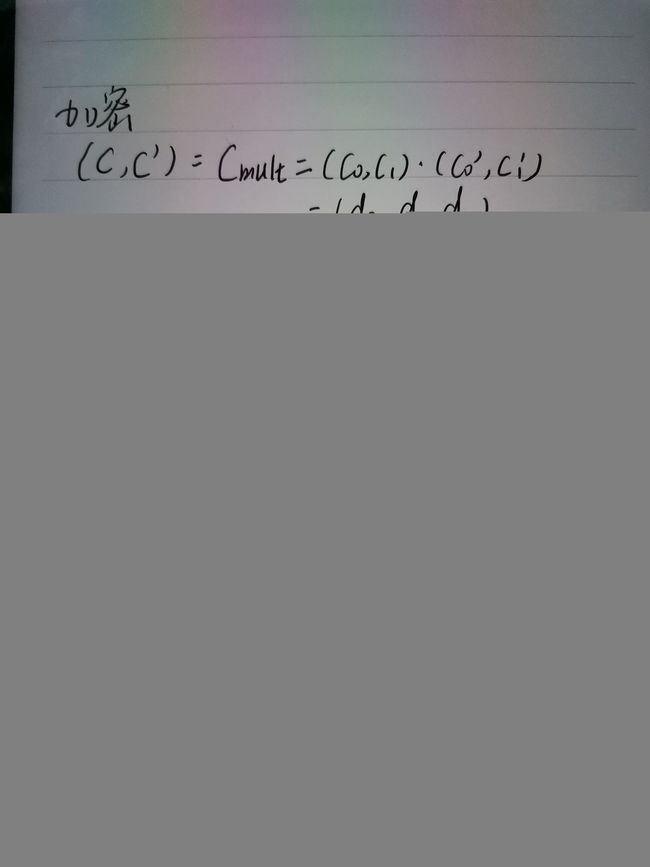2021SC@SDUSC PALISADE开源库（二）CKKS讲解系列（四）乘法和重新线性化

2021SC@SDUSC

目录

介绍

基本操作回顾

同态操作

加法操作

​ 乘法操作（明文 x 密文）

 密文 - 密文乘法

重新线性化

实现方法

 读者笔记

​ 密文x密文 与 重新线性化 结合

---

介绍

在上一篇文章 PALISADE开源库（二）CKKS讲解系列（三）加密和解密 中，我们看到了如何基于RLWE问题创建同态加密方案，实现了加法和密文 - 明文乘法。

虽然执行密文 - 明文乘法很容易，但正如我们将看到的，密文 - 密文要复杂得多。事实上，我们需要处理很多事情才能正确地完成它，例如找到正确的操作，以便一旦解密我们就得到两个密文的乘积，以及管理密文的大小。

因此，本文将介绍密文-密文乘法和重新线性化的概念，以减小产生的密文的大小。

基本操作回顾

为了了解我们将如何在 CKKS 中执行密文-密文乘法，让我们回顾一下我们在上一篇文章中看到的内容。

同态操作

加法操作

 乘法操作（明文 x 密文）

 密文 - 密文乘法

这就非常有趣了！如果我们思考一下，求 Decrypt(c, s) = c0 + c1.s 可以看作是对密钥s的多项式求值，它是形式为 c0+c1 的一次多项式。s是多项式变量。

因此，如果我们看到上图对两个密文乘积的解密操作，它可以看作是多项式 d0 + d1.s + d2.s² 在密钥s上计算二次方s²。

 因此，我们可以使用以下操作来进行密文-密文乘法:

此时密文多项式增加到了3个：

 

使用这样的操作是可行的，但是有一个问题：密文的大小在增长！实际上，虽然密文通常只有几个多项式，但这里我们有三个多项式。通过使用与之前相同的推理，如果我们什么都不做，要正确地解密下一个乘积，我们将需要5个多项式，然后是9个，以此类推。因此，密文的大小将呈指数增长，如果我们像这样定义密文-密文乘法，它将无法在实践中使用。

我们需要找到一种方法，在不增加每一步密文大小的情况下进行乘法运算。这就是重新线性化的作用所在!

重新线性化

所以我们可以定义密文之间的乘法运算为CMult(c, c') = (d0, d1, d2)。问题是，现在输出的是一个维数为3的密文，如果每次计算后都增加密文的大小，那么在实际应用中就不可行了。

实现方法

我们想一下，问题是什么?问题是我们需要第三项，d2项，用于多项式解密，DecryptMult(cmult, s) = d0 + d1.s + d2.s²。但如果我们能找到计算d2的方法呢。S2只有一次多项式作为常规解密?在这种情况下，密文的大小将是恒定的，它们都将只是两个多项式!

这就是重新线性化的本质:找到两个多项式(d '0, d '1)=Relin(cmult)，这样:

也就是说，重新线性化允许有一个多项式对，而不是三重，这样一旦它被使用常规的解密电路解密，只需要秘密密钥，而不需要它的平方，我们得到两个基础明文的乘法。 

因此，如果我们在每次密文-密文相乘后进行再线性化，我们将始终拥有相同大小的密文，具有相同的解密电路!

现在你可能想知道我们需要如何定义Relin来得到这样的结果。思路很简单，我们知道我们需要一些多项式使得d' 0 + d' 1.s=d0 + d1.s + d2.s²。这个想法是，我们将定义(d' 0, d' 1) = (d0, d1) + P，其中P表示一对多项式，使Decrypt(P ,s) = d2.s²。

这样，当我们计算(d' 0 ,d' 1)上的解密电路时，我们得到:

解密(d' 0, d' 1), s) = Decrypt((d0, d1), s) + Decrypt(P, s) = d0 + d1.s + d2.s²

让evk=(−a0.s + e0 + s², a0)，其中e0是一个小的随机多项式，a0是Rq上的均匀抽样多项式。则应用Decrypt(evk, s)=e0 + s² ≈ s²。这很好! 我们可以看到，由于基于RLWE问题很难提取出秘密，我们可以将评估密钥公开分享给执行计算的一方，它可以用来寻找平方项。

所以P是一个可能的候选，这个密文应该被解密为 d2.s² 可以是P = d2.evk = (d2.(−a0 + e0 + s²)，d2.a0)。实际上，正如我们看到的，我们有Decrypt(P,s)=d2.s² + d2.e0。那么我们可以像往常一样，考虑d2.s² + d2.e0 ≈ d2.s²吗?

不幸的是，我们不能这样做，因为d2.e0 项比通常的噪声大得多。如果你之前注意到，我们允许结果的近似，因为误差多项式很小，例如小多项式的和不会太影响结果。这里的问题是，d2会很大，因为它是d2=c1。c' 1每个c1包含一个多项式a在Rq上均匀采样，因此它比我们通常处理的小误差多项式要大得多。

所以，我们有:

P = ⌊P^(−1). d2.evk⌉(mod q)，这意味着我们将除以p并四舍五入到最接近的整数，取模q(而不是p q)。

我们终于找到了我们的候选人!因此，为了定义再线性化，我们需要一个评估键(可以公开，没有风险)，我们将其定义为:

 因此，如果我们有两个密文c,c '，我们想要将它们相乘(可能是几次)，然后解密结果，工作流程将是:

 读者笔记

 密文x密文 与 重新线性化 结合