地下水动力学--地下水水文学(持续更新)
地下水动力学—地下水水文学(持续更新)
部分内容转载自南方科技大学梁修雨教授地下水水文学讲课PPT
水文地质学英文及其含义
| 英文 | 中文 |
|---|---|
| stream | 流动,流出,小河,溪流 |
| flow | 流动 |
| streamflow | 河道汇流部分,单位m^3/s |
| runoff | 径流深,单位:mm |
| discharge | 流量 |
| baseflow | 基流 |
| evaporation | 蒸发 |
| recharge | 补给 |
| rainfall | 降雨 |
| catchment | 流域、集水处、聚水盆地 |
| throughfall | 穿透雨 |
| leakage | 渗漏 |
| infiltration | 入渗 |
| freshwater | 淡水 |
| continental | 大陆的,大洲的 |
| vadose zone | 包气带、渗流带 |
| overflow | 溢流 |
| overland flow | 地表径流 |
| diffuse | 四散的,散开的,弥散的 |
| watershed | 流域、分水岭、集水区 |
| water table | 潜水面 |
| subsurface | 次表面的,地下的 |
| the lumped parameter | 集总参数 |
| drainage basin/catchment | 流域 |
| watershed divide |
分水岭 |
| creek | 小溪,小河 |
| outflow constant | |
| recession constant | 退水常数 |
| specific yield | Sy 给水度 |
| specific storage | Ss |
| tributary | 支流 |
| fluvial | 河的、河流的、河中的 |
| S–specific capitiy | 贮水系数 |
| Ss–specific storage | 贮水率 |
| T–transmissivity | 导水系数 |
| Sy–specific yeild | 给水度 |
| D- hydraulic diffusivity | 水力扩散系数 |
| K–Permeability | 渗透系数 |

傅里叶变化的基础
ω = 2 π f \omega=2\pi f ω=2πf
ω \omega ω是角频率,f是频率
土壤水分特征曲线
土壤水分特征曲线是土壤含水量 θ \theta θ与土壤水吸力 ϕ \phi ϕ的关系曲线该曲线能够间接反映土壤孔隙大小的分布,分析不同质地土壤的持水性等。目前负压计法是测量土壤水吸力最简单最直观的方法,而时域反射法是测量土壤体积含水率的最常用最便捷的方法。

基模势是土壤含水量的函数,干燥土壤,吸力最大,随着土壤含水量的增加,吸力逐渐减小,当土壤含水量达到田间持水量时,吸力变为0,通常基模势的负值为吸力 ϕ \phi ϕ,同样的吸力,在脱水和吸水两个过程中,土壤吸持的水分数量是不同的,脱水过程过程吸持的水分要大于吸水过程吸持的水分,或者说,当土壤含水量一定时,脱水过程中相应的土壤吸力要大于吸水过程中相应的土壤吸力。
将土壤含水量和土壤吸力绘制成散点图,然后用经验公式拟合
下渗率:单位时间通过单位面积的土壤层面渗入到土壤的水量称为下渗率,常用单位为mm/min,mm/h。
下渗容量:
下渗容量随时间的变化曲线称为下渗曲线。
饱和土壤的达西定量
v = K I v=KI v=KI
渗透系数也称水力传导系数,渗透系数具有速度的量纲,常用cm/s或m/d
控制非饱和土壤水流运动的因素与控制饱和土壤水流运动的的因素有所不同,一是两者的总势组成不同,在饱和土壤中,总势由重力势和静水压力势组成,而在非饱和土壤中,总势则由重力势和基模势组成;二者的水力传导度不同,饱和水力传导度是一个常数,非饱和水力传导度是土壤含水量的函数,干燥土壤的水力传导度最小,随着土壤含水量的增加,水力传导度也增加,当土壤含水量达到饱和时,水力传导度也达到最大,此时即为饱和水力传导度。
线性和非线性偏微分方程
如果偏微分方程中,未知函数及它的所有偏导数都是线性的,且方程中的系数都依赖于自变量(或者是常数),那么这样的偏微分方程就称为线性偏微分方程,特别的,如果方程中的系数都是常数,则称为常系数偏微分方程,显然,如果方程中的系数是自变量的函数,则称为变系数偏微分方程,方程中如果出现未知函数及偏导数不是线性的,则称为非线性偏微分方程。
各阶微分项有次数高于1的微分方程即为非线性偏微分方程。
扩散率为常数时的下渗方程:
{ ∂ θ ∂ t = D ∂ 2 θ ∂ Z 2 θ ( z , 0 ) = θ 0 θ ( 0 , t ) = θ n lim z → ∞ θ ( z , t ) = θ 0 \left\{ \begin{aligned} \frac{\partial{\theta}}{\partial{t}}=D\frac{\partial^2{\theta}}{\partial{Z^2}} \\ \theta(z,0)=\theta_0 \\ \theta(0,t)=\theta_n\\ \lim_{z\to\infty}{\theta(z,t)}=\theta_0 \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∂t∂θ=D∂Z2∂2θθ(z,0)=θ0θ(0,t)=θnz→∞limθ(z,t)=θ0
上式可以使用laplace变换进行求解。
土壤中三相关系
V t V_t Vt为土块的总体积
V s V_s Vs为固相体积
V w V_w Vw为液相体积
V a V_a Va为气相体积
V f V_f Vf土壤中孔隙的容积
则有:
V f = V w + V a V_f=V_w+V_a Vf=Vw+Va
V t = V s + V w + V a V_t=V_s+V_w+V_a Vt=Vs+Vw+Va
M t M_t Mt为土块的总质量
M s M_s Ms为固相质量
M w M_w Mw为液相质量
M a M_a Ma为气相质量,其中 M a = 0 M_a=0 Ma=0
与土壤三相有关的土壤物理量
固体密度:土壤中固体颗粒的质量与固相容积的比值
干容重:土壤中固体颗粒的质量与土块总体积的比值
孔隙度:土块中孔隙容积与土块总容积之比
孔隙比:土块中孔隙容积与固体颗粒容积之比
土壤含水量
土壤含水量描述土壤中含有水分的情况,又称土壤湿度,他有几种表示方法,
- 质量含水率
- 容积含水量
- 饱和度
土壤水的存在形态
分子力**
土壤水分常数
最大吸湿量(吸湿系数):在水汽达到饱和的空气中,干燥土壤的吸湿水达到最大数量时的土壤水量
最大分子持水量:
凋萎系数
毛管断裂含水量
田间持水量
饱和含水量
土壤水分剖面
土壤含水率沿深度方向的变化曲线称为土壤水分剖面
它描述了土壤含水率在深度方向的分布情况,故又称土壤含水率垂向分布,根据土壤水分剖面,可以计算出土壤中任一土层,以水深计的含水量。
土壤水分剖面图
下渗曲线
下渗现象的定量表示是下渗率,单位时间通过单位面积的土壤层面渗入到土壤中的水量称为下渗率。单位mm/min或mm/h
如果供水强度充分大,则下渗速率将达到同初始土壤含水量和同土壤质地,结构条件下的最大值,称为下渗能力或下渗容量,
下渗容量随时间的变化曲线称为下渗曲线。
下渗曲线是一条递减曲线,分为
- 渗润阶段:土壤含水量较小,下渗容量较大,下渗容量随时间迅速递减
- 渗漏阶段:土壤含水量不断增加,下渗容量明显减小,下渗容量随时间递减变得缓慢
- 渗透阶段:土壤含水量达到田间持水量以上,下渗容量变得稳定,达到下渗容量最小值,为稳定下渗率。
土壤水分剖面的四分带
最上层为饱和带,一般厚度不大,不到1.5cm,饱和带以下为水分传递带,这是一个土壤含水量沿深度分布比较均匀,、厚度较大的非饱和土层,厚度随供水是时间的增长而不断增加,土壤含水量介于田间持水量和饱和含水量之间,水分传递带以下为湿润带,他是连接水分传递带和湿润峰的水分带。在这一带中,土壤含水量随深度迅速减小,湿润带与下渗水未涉及到的土壤的交界面称为湿润峰。在湿润峰处,土壤含水量梯度很大。
控制非饱和土壤水流运动的因素与控制饱和土壤水流运动的因素有所不同。一是二者的总势组成不同,在饱和土壤中,总势由重力势和静水压力势组成,而在非饱和土壤中,总势由重力势和基模势组成;二是二者的水力传导度不同,饱和水力传导度是一个常数,非饱和水力传导度是土壤含数量的函数,干燥土壤的水力传导度最小,随着土壤含水量的增加,水力传导度也增加,当土壤含水量达到饱和时,水力传导度也达到最大,此即为饱和水力传导度。
对于理查兹方程,只要已知土壤水分特征曲线 Ψ − θ \Psi-\theta Ψ−θ,和水力传导度与土壤含水量的关系曲线 K ( θ ) − θ K(\theta)-\theta K(θ)−θ
并给定适当的初始条件和边界条件,就可由Richards方程求解各种非饱和水流运动问题。
拉普拉斯变换
F ( s ) = L { f ( t ) } = ∫ 0 + ∞ f ( t ) e − s t d t F(s)=\mathcal{L}\left\{{f(t)} \right\} =\int_{0}^{+\infty}{f(t)e^{-st}dt} F(s)=L{f(t)}=∫0+∞f(t)e−stdt
![]()

使用拉普拉斯变换求解常微分方程
x ′ ′ ′ + 3 x ′ ′ + 3 x ′ + x = 6 e − 1 x^{'''}+3x^{''}+3x^{'}+x=6e^{-1} x′′′+3x′′+3x′+x=6e−1
玻尔兹曼变换解微分方程
水循环(hydrologic cycle)
降水落到地表后进入到不同的水循环途径,一部分暂时以冰或雪的形式留在地表或汇入洼地,后者称洼地蓄水(depression storage),部分河流中的水来自地表径流或者渗入河床的地下水,河流中来自地下水的部分称为基流(baseflow)
导水系数:含水层的渗透系数与其厚度的乘积
含水层响应时间:
the characteristic aquifer response time
是指由降雨到含水层接受补给的时间,在干旱区特征响应时间可能会特别长。
系统在单位冲激函数激励下引起的零状态响应被称之为该系统的冲激响应,他与系统的传递函数互为傅里叶变换的关系。
时间尺度
水分特征曲线斜率的倒数,表示单位基质势的变化所引起的土壤含水率的变化。称为容水度。
C = d θ d ϕ m C=\frac{d\theta}{d\phi_m} C=dϕmdθ
田间持水量:在长时间的重力排水后仍然保留在土中的水量
土壤含水率 θ \theta θ与非饱和导水率 K K K、垂向位置z,土壤基质势 Φ \Phi Φ,土壤重力势 h h h,时间t的相互关系
- 土壤含水率是位置和时间的函数——
- 非饱和导水率是位置和时间的函数——
- 土壤基质势是——
- 土壤重力势是———
含水层的释水能力为S,(storativity),分为specific storage 和 specific yield
给水度:单位面积的含水层,当潜水面下降一个单位长度时,在重力作用下所能释放出的水量
比蓄水量: 是指蓄水层的一部分在保持完全饱和的情况下,每单位质量或体积的蓄水层,每单位水头变化释放的水量。
承压含水层基本微分方程
throughfall净降水量
baseflow 激流
streamflow 径流,河流流量,河川流量
runoff flow径流
1. Darcy’s law
hydraulic head
hydraulic gradient
seepage velocity 渗透速率
Q = − K A I = − K A d h d l Q=-KAI=-KA\frac{dh}{dl} Q=−KAI=−KAdldh
v = K I v=KI v=KI
gravity 重力势
pressure gradient 压力梯度
kinetic energy 动能
gravitational potential energy
fluid pressural energy
理想流体,管道流,伯努利方程
Φ = g z + P ρ + v 2 2 \Phi=gz+\frac{P}{\rho}+\frac{v^2}{2} Φ=gz+ρP+2v2

把机械能除以g,单位重量的机械能
Φ = z + P ρ g + v 2 2 g \Phi=z+\frac{P}{\rho g}+\frac{v^2}{2g} Φ=z+ρgP+2gv2

elevation head
pressure head
velocity head
Q = K A Δ h L Q=KA\frac{\Delta h}{L} Q=KALΔh

10m water head—> 8m
reason: 粘滞力
seepage velocity is usually small, velocity head can be ignored
hydrualic head
Piezometer测压计
tensiometer张力计
tube
pipe
datum:基准点
通常以海平面作为基准点
h = z + τ h=z+\tau h=z+τ
h ( x , y , z , t ) h(x,y,z,t) h(x,y,z,t)
地下水的流动只与总水头有关,与压力和重力水头单一无关。
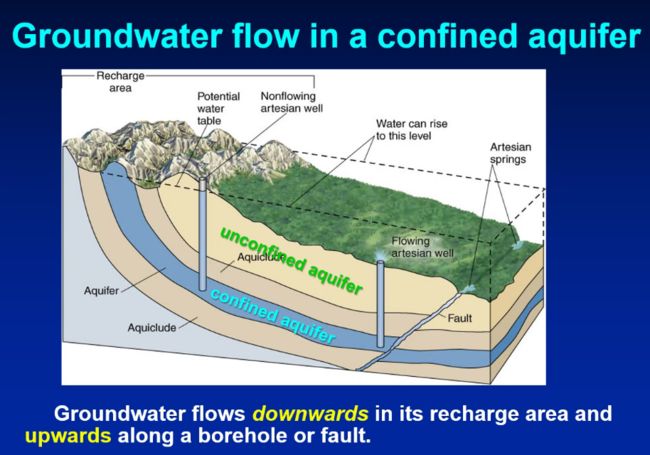
Aquiclude弱透水层
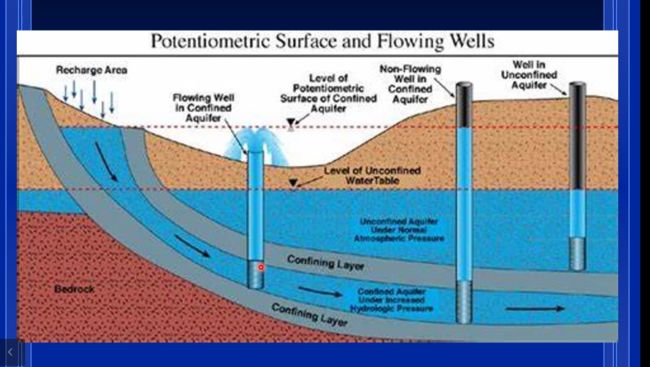
flowing aresain well 自流井
aresain spring自流泉
fresh water head
density is larger
the pressure head is lower
fresh water vs. saltwater
vs.
versus对抗,对应
20cm的海水水头相当于20.5cm的淡水水头
Measure hydrualic head in field
datum基准点
water table depth 地下水埋深
地下水位越高,埋深越低
井口高程

h = z c = d w t h=z_c=d_{wt} h=zc=dwt
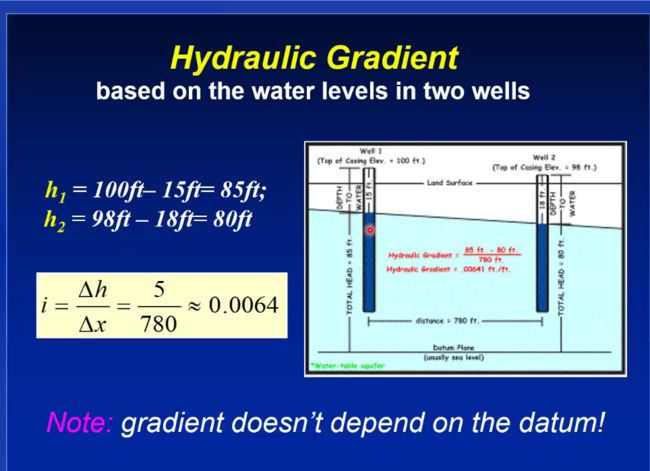
hydrualic gradient
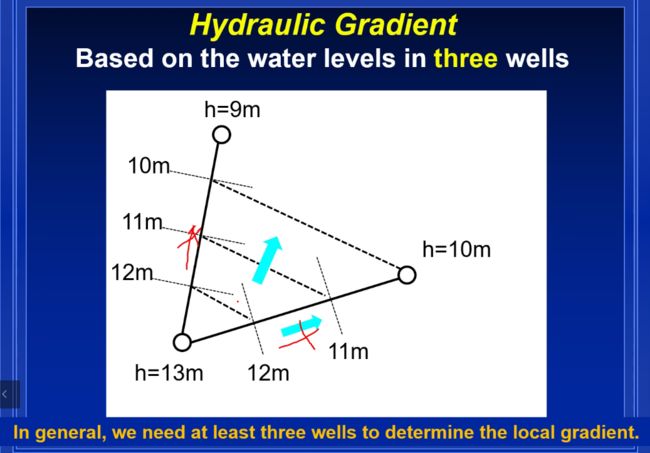
流线与水头等值线垂直
水沿着水头下降最大的方向流动
至少三口井才能确定地下水的唯一流向
水力梯度的确定方法
等水头线都是平行的
水力梯度是矢量
水向下流
seepage velocity
Darcy velocity
含水层的分布
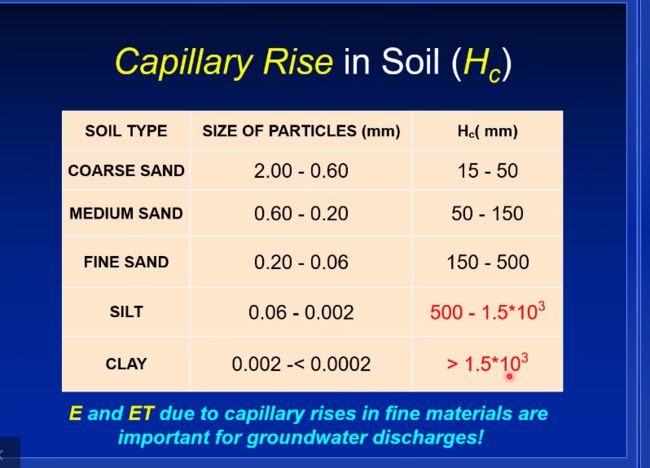
capillary fringe
毛细上升带
土壤含水率=体积含水率=土壤湿度
θ = V w V \theta=\frac{V_w}{V} θ=VVw
在非饱和带中
θ < 孔 隙 度 \theta<孔隙度 θ<孔隙度
饱和带
θ = 孔 隙 度 \theta=孔隙度 θ=孔隙度
实际的土壤含水率在非饱和带中的分布
饱和和非饱和带的水头分布
饱和带压力水头小于0
非饱和带压力水头大于0
capillary fringe毛细带
支持毛细力
管子越细,上升越高
毛细上升如果高,根系则可以吸水多
蒸散发也越多
Aquifer含水层
Aquitard弱透水层
perched water-table aquifer
上层滞水
unconfined aquifer潜水含水层
confined aquifer承压含水层
湿润地区
潜水含水层易受污染
confined bed承压板=aquitard
benath在……下方,在什么下面
alluvium fans冲积扇
canyon峡谷
承压含水层的给水系数小于潜水含水层
SW basin
Surface water basin
承压含水层矿化度高,盐分高
流域边界
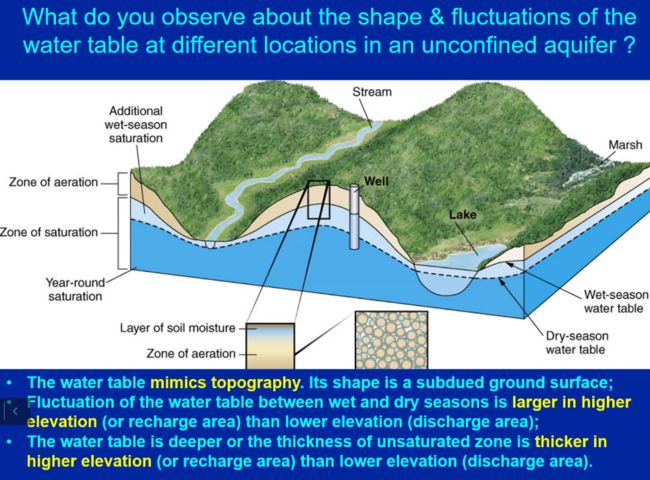
潜水含水层的水位和地形基本一致
地表水像相当于潜水含水层的露头
mimics topography
模仿地形
subdued 克制,征服、克服、控制
leaky aquifer 越流含水层 = semi-confined aquifer 半承压含水层
Aquifer compressibility and Storativity
承压含水层中的水的释放机制
dewatering
承压含水层的水的来源就是压力释放
不是来自于两边补给
如果稳定来自于两边补给,不会形成降落漏斗状
承压含水层的弹性释水
潜水含水层的重力释水
弹性模量的导数就是压缩系数的导数
压缩系数就是单位应力变化导致的应变。
应力,物理内部单位面积受到的的力

c o m p r e s s i b i l i t y = d d σ compressibility=\frac{d}{d \sigma} compressibility=dσd

水的状态方程
一定的压力下水的密度是多少?
atmospheric大气压
多孔介质的压缩系数
在压缩过程中,水被压缩 、固体颗粒被压缩、孔隙被压缩(颗粒的排列方式更紧了,packing)。
effective stress有效应力
σ T = σ e + p \sigma_T=\sigma_e+p σT=σe+p
作用在土壤骨架上的作用力
change in effective stress
when dewatering, p decrease,
effective stress increase.
d σ e = − d p d\sigma_e=-dp dσe=−dp

压 强 = ρ g 乘 以 压 力 水 头 压 力 水 头 = 总 水 头 − 位 置 水 头 h − z 压强=\rho g乘以压力水头\\ 压力水头=总水头-位置水头\\ h-z 压强=ρg乘以压力水头压力水头=总水头−位置水头h−z
建立了有效应力的变化与地下水位变化 的联系
有效应力增加导致固体颗粒被压缩
c o m p r e s s i b i l i t y = α compressibility=\alpha compressibility=α
α = − d V T / V T d σ e \alpha=-\frac{dV_T/V_T}{d\sigma_e} α=−dσedVT/VT

体积的变化理解成含水层厚度的变化。
孔隙比=孔隙的体积/固体颗粒的体积
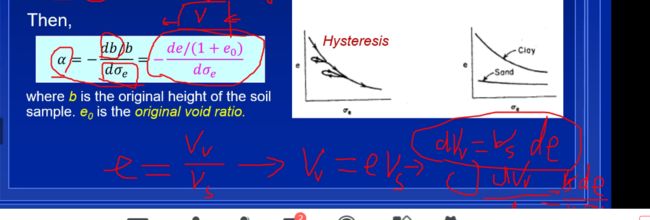
粘土的压缩系数大于砂

α = − d b / b d σ e \alpha=-\frac{db/b}{d\sigma_e} α=−dσedb/b
d σ e = = ρ g d h d\sigma_e==\rho gdh dσe==ρgdh
then:
d b = − α b d σ e = α b ρ g d h db=-\alpha bd\sigma_e=\alpha b \rho gdh db=−αbdσe=αbρgdh
建立了水位变化对应的含水层厚度变化的关系
则可以反映地面沉陷量。
for water
ρ , μ , β \rho,\mu,\beta ρ,μ,β
for porous media
n , k , α n,k,\alpha n,k,α
α 和 β 分 别 为 固 体 颗 粒 和 水 的 压 缩 系 数 \alpha和\beta分别为固体颗粒和水的压缩系数 α和β分别为固体颗粒和水的压缩系数
specific yeild S y S_y Sy 潜水的重力给水度
单位面积的水柱水头下将一个单位释放出的水量
specific storage S s S_s Ss承压含水层
贮水率/弹性释水率
单位体积的含水层水头下降一个单位释放的水流
S s = V w / V T d h S_s=\frac{V_w/V_T}{dh} Ss=dhVw/VT
![]()
S s = ρ g ( α + n β ) , , 量 纲 1 / L S_s=\rho g(\alpha+n\beta),,量纲1/L Ss=ρg(α+nβ),,量纲1/L

S s S_s Ss的范围
Storativity S S S 贮水系数/释水系数
贮水率乘以含水层厚度
导水系数 T T T
渗透系数乘以含水层厚度
cone of depression
降落漏斗
Subsidence 沉陷
地下水流动方程
Grounwater flow equation
scalar, vector, tensor
标量、向量、张量
Hydraulic conductivity tensor
Darcy’s law in 3D
h ( x , y , z , t ) h(x,y,z,t) h(x,y,z,t)
PDE偏微分方程
recall Taylor formula
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + … … 加 一 个 高 阶 无 穷 小 o ( x − x 0 ) f(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+…… 加一个高阶无穷小o(x-x_0) f(x)=f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+……加一个高阶无穷小o(x−x0)
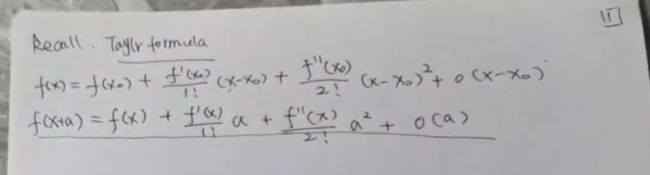
f ( x + a ) = f ( x ) + f ′ ( x ) 1 ! a + f ′ ′ ( x ) 2 ! a 2 + … … 加 一 个 高 阶 无 穷 小 o ( a ) f(x+a)=f(x)+\frac{f'(x)}{1!}a+\frac{f''(x)}{2!}a^2+……\\ 加一个高阶无穷小o(a) f(x+a)=f(x)+1!f′(x)a+2!f′′(x)a2+……加一个高阶无穷小o(a)
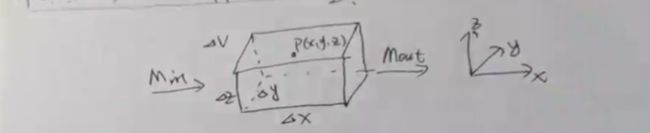
principle I: mass balance
M m i n − M m a x = ∂ M ∂ t M_{min}-M_{max}=\frac{\partial M}{\partial t} Mmin−Mmax=∂t∂M
X direction:
M X = ρ V x = ρ v x Δ y Δ z 中 心 点 处 的 流 量 , v x ( x , y , z ) , 不 同 处 流 速 不 同 M i n X = ρ v x ( x − Δ x 2 , y , z ) Δ y Δ z M^X=\rho V_x=\rho v_x \Delta y\Delta z\\ 中心点处的流量,v_x(x,y,z),不同处流速不同\\ M_{in}^X=\rho v_x(x-\frac{\Delta x}{2},y,z) \Delta y\Delta z MX=ρVx=ρvxΔyΔz中心点处的流量,vx(x,y,z),不同处流速不同MinX=ρvx(x−2Δx,y,z)ΔyΔz
ρ v x ( x − Δ x 2 , y , z ) = ρ v x ( x , y , z ) + ∂ ( ρ v x ) ∂ x 1 1 ! ( − Δ x 2 ) 忽 略 二 阶 及 以 上 \rho v_x(x-\frac{\Delta x}{2},y,z)=\rho v_x(x,y,z)+\frac{\partial (\rho v_x)}{\partial x}\frac{1}{1!}(\frac{-\Delta x}{2})\\ 忽略二阶及以上 ρvx(x−2Δx,y,z)=ρvx(x,y,z)+∂x∂(ρvx)1!1(2−Δx)忽略二阶及以上
ρ v x ( x + Δ x 2 , y , z ) = ρ v x ( x , y , z ) + ∂ ( ρ v x ) ∂ x 1 1 ! ( Δ x 2 ) 忽 略 二 阶 及 以 上 \rho v_x(x+\frac{\Delta x}{2},y,z)=\rho v_x(x,y,z)+\frac{\partial (\rho v_x)}{\partial x}\frac{1}{1!}(\frac{\Delta x}{2})\\ 忽略二阶及以上 ρvx(x+2Δx,y,z)=ρvx(x,y,z)+∂x∂(ρvx)1!1(2Δx)忽略二阶及以上
So X direction:
M i n X − M o u t X = − ∂ ρ v x ∂ x Δ x Δ y Δ z M^X_{in}-M^X_{out}=-\frac{\partial \rho v_x}{\partial x}\Delta x\Delta y\Delta z MinX−MoutX=−∂x∂ρvxΔxΔyΔz
So Y direction:
M i n Y − M o u t Y = − ∂ ρ v y ∂ y Δ x Δ y Δ z M^Y_{in}-M^Y_{out}=-\frac{\partial \rho v_y}{\partial y}\Delta x\Delta y\Delta z MinY−MoutY=−∂y∂ρvyΔxΔyΔz
So Z direction:
M i n Z − M o u t Z = − ∂ ρ v z ∂ z Δ x Δ y Δ z M^Z_{in}-M^Z_{out}=-\frac{\partial \rho v_z}{\partial z}\Delta x\Delta y\Delta z MinZ−MoutZ=−∂z∂ρvzΔxΔyΔz
Total:
M i n − M o u t = − [ ∂ ρ v x ∂ x + ∂ ρ v y ∂ y + ∂ ρ v z ∂ z ] Δ x Δ y Δ z = ∂ M ∂ t M_{in}-M_{out}=-[\frac{\partial \rho v_x}{\partial x}+\frac{\partial \rho v_y}{\partial y}+\frac{\partial \rho v_z}{\partial z}]\Delta x\Delta y\Delta z=\frac{\partial M}{\partial t} Min−Mout=−[∂x∂ρvx+∂y∂ρvy+∂z∂ρvz]ΔxΔyΔz=∂t∂M
− ρ [ ∂ v x ∂ x + ∂ v y ∂ y + ∂ v z ∂ z ] Δ V − [ v x ∂ ρ x + v y ∂ ρ y + v z ∂ ρ z ] Δ V = ∂ M ∂ t -\rho[\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}]\Delta V-[v_x\frac{\partial \rho}{x}+v_y\frac{\partial \rho}{y}+v_z\frac{\partial \rho}{z}]\Delta V=\frac{\partial M}{\partial t} −ρ[∂x∂vx+∂y∂vy+∂z∂vz]ΔV−[vxx∂ρ+vyy∂ρ+vzz∂ρ]ΔV=∂t∂M
− ρ [ ∂ v x ∂ x + ∂ v y ∂ y + ∂ v z ∂ z ] Δ V = ∂ M ∂ t -\rho[\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}]\Delta V=\frac{\partial M}{\partial t} −ρ[∂x∂vx+∂y∂vy+∂z∂vz]ΔV=∂t∂M
recall specific storage
S_s
S s = ∂ V W Δ V ∂ h S_s=\frac{\partial V_W}{\Delta V \partial h} Ss=ΔV∂h∂VW
∂ M ∂ t = ∂ ρ V W ∂ t = ∂ ρ V W ∂ h ∂ h ∂ t = ρ Δ V S s ∂ h ∂ t \frac{\partial M}{\partial t}=\frac{\partial \rho V_W}{\partial t}=\frac{\partial \rho V_W}{\partial h}\frac{\partial h}{\partial t}=\rho \Delta VS_s\frac{\partial h}{\partial t} ∂t∂M=∂t∂ρVW=∂h∂ρVW∂t∂h=ρΔVSs∂t∂h
− [ ∂ v x ∂ x + ∂ v y ∂ y + ∂ v z ∂ z ] = S s ∂ h ∂ t -[\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}]=S_s\frac{\partial h}{\partial t} −[∂x∂vx+∂y∂vy+∂z∂vz]=Ss∂t∂h
达西定律:
v x = − K x ∂ h ∂ x v_x=-K_x\frac{\partial h}{\partial x} vx=−Kx∂x∂h
带入三个方向
[ ∂ ∂ x ( K x ∂ h ∂ x ) + ∂ h ∂ y ( K y ∂ h ∂ y ) + ∂ h ∂ z ( K z ∂ h ∂ z ) ] = S s ∂ h ∂ t [\frac{\partial}{\partial x}(K_x\frac{\partial h}{\partial x})+\frac{\partial h}{\partial y}(K_y\frac{\partial h}{\partial y})+\frac{\partial h}{\partial z}(K_z\frac{\partial h}{\partial z})]=S_s\frac{\partial h}{\partial t} [∂x∂(Kx∂x∂h)+∂y∂h(Ky∂y∂h)+∂z∂h(Kz∂z∂h)]=Ss∂t∂h
以上即为控制方程PDE
Governing equation G.E.
3D , heterogeneous, anisotropic, transient , groundwater flow.
heterogeneous
K是x,y,z的函数
homogeneous
K is a constant in space
Steady state稳态
h and v is constant in time.
以上基于质量守恒和达西定律
初始条件和边界条件来解微分方程。两者称为定解条件
initial condition
boundary condition
governing equation
parameters
analytical
numerical
- soluiton.
B.C.
First type (Dirchlet)
h ( x , y , z , t ) = H b ( x , y , z , t ) 边 界 处 的 水 头 已 知 h(x,y,z,t)=H_b(x,y,z,t) \\ 边界处的水头已知 h(x,y,z,t)=Hb(x,y,z,t)边界处的水头已知
Second type(Neuman)
− K ∂ h ∂ n = Q b ( x , y , z , t ) 边 界 处 的 流 量 或 者 水 头 的 导 数 已 知 -K\frac{\partial h}{\partial n}=Q_b(x,y,z,t)\\ 边界处的流量或者水头的导数已知 −K∂n∂h=Qb(x,y,z,t)边界处的流量或者水头的导数已知
Third type(Cauchy)
简化模型
simplification
- steady-state flow
[ ∂ ∂ x ( K x ∂ h ∂ x ) + ∂ h ∂ y ( K y ∂ h ∂ y ) + ∂ h ∂ z ( K z ∂ h ∂ z ) ] = 0 h ( t ) = c , v ( t ) = c , h ( x , y , z ) ≠ c , v ( x , y , z ) ≠ c [\frac{\partial}{\partial x}(K_x\frac{\partial h}{\partial x})+\frac{\partial h}{\partial y}(K_y\frac{\partial h}{\partial y})+\frac{\partial h}{\partial z}(K_z\frac{\partial h}{\partial z})]=0 \\ h(t)=c,v(t)=c,h(x,y,z)\ne c,v(x,y,z)\ne c [∂x∂(Kx∂x∂h)+∂y∂h(Ky∂y∂h)+∂z∂h(Kz∂z∂h)]=0h(t)=c,v(t)=c,h(x,y,z)=c,v(x,y,z)=c
-
homogeneous, anisotropic
[ K x ∂ ∂ x ( ∂ h ∂ x ) + K y ∂ h ∂ y ( ∂ h ∂ y ) + K z ∂ h ∂ z ( ∂ h ∂ z ) ] = S s ∂ h ∂ t [K_x\frac{\partial}{\partial x}(\frac{\partial h}{\partial x})+K_y\frac{\partial h}{\partial y}(\frac{\partial h}{\partial y})+K_z\frac{\partial h}{\partial z}(\frac{\partial h}{\partial z})]=S_s\frac{\partial h}{\partial t} [Kx∂x∂(∂x∂h)+Ky∂y∂h(∂y∂h)+Kz∂z∂h(∂z∂h)]=Ss∂t∂h -
homogeneous, isotropic
K [ ∂ ∂ x ( ∂ h ∂ x ) + ∂ h ∂ y ( ∂ h ∂ y ) + ∂ h ∂ z ( ∂ h ∂ z ) ] = S s ∂ h ∂ t K[\frac{\partial}{\partial x}(\frac{\partial h}{\partial x})+\frac{\partial h}{\partial y}(\frac{\partial h}{\partial y})+\frac{\partial h}{\partial z}(\frac{\partial h}{\partial z})]=S_s\frac{\partial h}{\partial t} K[∂x∂(∂x∂h)+∂y∂h(∂y∂h)+∂z∂h(∂z∂h)]=Ss∂t∂h
laplace 算子
K ▽ 2 h = S s ∂ h ∂ t K\bigtriangledown ^2h=S_s\frac{\partial h}{\partial t} K▽2h=Ss∂t∂h
2-D problem
[ ∂ K x ∂ x ( ∂ h ∂ x ) + ∂ h ∂ y ( K y ∂ h ∂ y ) ] = S s ∂ h ∂ t [\frac{\partial}{K_x\partial x}(\frac{\partial h}{\partial x})+\frac{\partial h}{\partial y}(\frac{K_y\partial h}{\partial y})]=S_s\frac{\partial h}{\partial t} [Kx∂x∂(∂x∂h)+∂y∂h(∂yKy∂h)]=Ss∂t∂h
PDE是一般性方程,不限制于潜水和承压,描述水面以下任意位置为微元体的控制方程
2-D confined aquifer horizontal
b K ( ∂ 2 h ∂ x 2 + ∂ t 2 h ∂ y 2 ) = b S S ∂ h ∂ t T ( ∂ 2 h ∂ x 2 + ∂ 2 h ∂ y 2 ) = b S ∂ h ∂ t bK(\frac{\partial^2 h}{\partial x^2}+\frac{\partial t^2 h}{\partial y^2})=bS_S\frac{\partial h}{\partial t}\\ T(\frac{\partial^2 h}{\partial x^2}+\frac{\partial^2 h}{\partial y^2})=bS\frac{\partial h}{\partial t}\\ bK(∂x2∂2h+∂y2∂t2h)=bSS∂t∂hT(∂x2∂2h+∂y2∂2h)=bS∂t∂h
量纲
T【 L 2 / T L^2/T L2/T】
S【-】