OpenCV学习笔记13_霍夫变换
文章目录
- 霍夫变换的原理:
-
- 1、检测直线
- 推导过程:
- 2、检测圆
- 二、OpenCV中的函数:
-
- 累计概率霍夫变换
- 霍夫变换检测圆
- 三、代码:
霍夫变换的原理:
1、检测直线
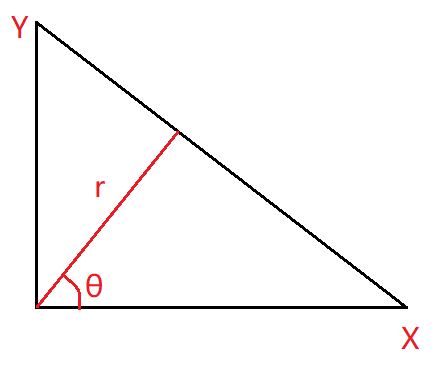
y = ( − c o s θ / s i n θ ) x + ( r / s i n θ ) y=(-cosθ/sinθ )x+(r/sinθ ) y=(−cosθ/sinθ)x+(r/sinθ)
r = x c o s θ + y s i n θ r=x cosθ+y sinθ r=xcosθ+ysinθ
推导过程:
直线y=kx+b为斜率为k截距为b的直线,假设已知一个点(m,n)在直线上,
代入直线方程那么n=mk+b,转换一下形式得k=n/m-b/m,m与n为常数,上式变为k=C1b+C2。
图像为:

当k=k0,b=b0时三条线相交,则三点在k=k0,b=b0时候在同一直线上,由此可判断各点是否在一条直线上。
霍夫变换检测直线就是列出所有点的k,b坐标系方程,
找出相交的线,对应的点就在一个直线上。
由于k的范围为[0,无穷),后续投票箱算法无法对无穷的k投票。
所以改为
r=x cosθ+y sinθ
其中r为原点到直线的垂线的长度,θ为r相对于横轴的角度。
具体实现方法分为7步:
1、设置θ与r的步长(r最大值为图像对角线长度);
2、建立r与θ的投票箱(二维数组);
3、根据步长算出每个点的θ值与r值;
4、投票箱一一对应计算出的θ值与r值如果相同则加1;
5、设置数量阈值;
6、获取数组中值大于阈值的数的θ与r值;
7、通过当前θ与r画出直线。
注意:需要理解的一点是笛卡尔坐标系下的一条直线的θ与r值(r垂直于直线)在极坐标系下是不变的。
霍夫变换检测直线有两个参数(θ值与r值);
霍夫变换检测圆需要三个参数(圆心坐标值(x0,y0),半径r值)
2、检测圆
步骤为(霍夫梯度法):
1、使用sobel算子得到图像的梯度值,得出梯度方向;
2、在所有检测到的点的在梯度方向上画出直线;
3、建立圆心点坐标投票箱;
4、建立圆心坐标点与半径r的投票箱;
5、设置圆心坐标投票箱的数量阈值;
6、找出直线相交大于阈值的点为待选圆心;
7、计算所有点距离待选圆心的距离;
8、设置圆心与半径投票箱的阈值;
9、非极大值抑制。
二、OpenCV中的函数:
①普通霍夫变换;
CV_EXPORTS_W void HoughLines(
InputArray image,
OutputArray lines,
double rho, double theta, int threshold,
double srn = 0, double stn = 0,
double min_theta = 0, double max_theta = CV_PI );
参数解释:
1、InputArray image:输入图像,8位的二值图;
2、OutputArray lines:存放2或3个元素的vector,(r,θ )或(r,θ,vote(投票数));
3、double rho:r的最小步长(像素距离分辨率);
4、double theta:θ的最小分辨率,θ的范围为[0,360],一般取1度,也就是pi/180;
5、int threshold:交点个数阈值,小于阈值的交点忽略;
6、double srn = 0:对于多尺度 hough 变换,它是距离分辨率r的除数;
7、double stn = 0:对于多尺度 hough 变换,它是角度分辨率θ的除数;
8,9、double min_theta = 0, double max_theta = CV_PI:θ的最大最小值;
使用步骤:
1、将源图像转化为灰度图,使用边缘检测算子检测边缘并返回二值检测图;
2、设置接收vector,使用HoughLines函数,设置HoughLines函数的参数;
3、接收到lines之后循环将点画到源图像上,具体操作为:
假设已知θ与r,可以求出待求线的垂直交点坐标为r0(rcos(θ),rsin(θ));
根据直线求斜率的一些定理:
s i n ( π / 2 − θ ) / c o s ( π / 2 − θ ) = ( n s i n θ ) / ( − n c o s θ ) = k sin(π/2-θ)/cos(π/2-θ) =(n sinθ)/(-ncosθ )=k sin(π/2−θ)/cos(π/2−θ)=(nsinθ)/(−ncosθ)=k
而:
( Y 1 − r s i n θ ) / ( X 1 − r c o s θ ) = k (Y_1-r sinθ)/(X_1-r cosθ )=k (Y1−rsinθ)/(X1−rcosθ)=k
假设
Y 1 − r s i n θ = n s i n θ Y_1-r sinθ= n sinθ Y1−rsinθ=nsinθ
X 1 − r c o s θ = − n c o s θ X_1-r cosθ=-ncosθ X1−rcosθ=−ncosθ
(相当于两点间的最小距离设为了1,再扩大n倍,相应坐标也扩大,线段长度也扩大)
则可以在r0点向上或向下找到不同两个在此直线上的点,画出相应的直线;
具体代码:
double x_0 = r*cos(theta);
double y_0 = r*sin(theta);
Point P1, P2;
P1.x = cvRound(x_0 + 1000 * sin(theta));//四舍五入
P1.y = cvRound(y_0 - 1000 * cos(theta));
P2.x = cvRound(x_0 - 1000 * sin(theta));
P2.y = cvRound(y_0 + 1000 * cos(theta));
line(src, P1, P2, Scalar(255, 0, 0));
累计概率霍夫变换
函数定义:
CV_EXPORTS_W void HoughLinesP(
InputArray image,
OutputArray lines,
double rho, double theta, int threshold,
double minLineLength = 0, double maxLineGap = 0 );
参数解释:
1、InputArray image:输入图像,8位的二值图;
2、OutputArray lines:存放4个元素的vector,(x1,y1,x2,y2);
3、double rho:r的最小步长(像素距离分辨率);
4、double theta:θ的最小分辨率,θ的范围为[0,360],一般取1度,也就是pi/180;
5、int threshold:交点个数阈值,小于阈值的交点忽略
6、minLinLength: 能组成一条直线的最少点的数量. 点数量不足的直线将被抛弃.线段的最小长度
7、maxLineGap:线段上最近两点之间的阈值
因为接收的lines为x1,y1,x2,y2两端点的坐标:
所以可直接使用cv::Point类型设置x与y值;
霍夫变换检测圆
函数定义:
CV_EXPORTS_W void HoughCircles(
InputArray image, OutputArray circles,
int method, double dp, double minDist,
double param1 = 100, double param2 = 100,
int minRadius = 0, int maxRadius = 0 );
参数解释:
1、InputArray image:输入图像为8位单通道灰度图;
2、OutputArray circles:3个或4个元素的vector,(x, y, radius),圆心坐标与半径;
3、int method:使用的运算方法;有霍夫梯度法等
4、Double dp:dp = 1; 输入图像与累加器分辨率的比值,且此参数允许创建一个比输入图像分辨率低的累加器。例如,如果dp= 1时,累加器和输入图像具有相同的分辨率。如果dp=2,累加器便有输入图像一半那么大的宽度和高度。
5、Double mindist: 检测到的圆心之间的最小距离。如果参数太小,除了一个真实的圆之外,多个相邻圆可能会被错误地检测到。如果太大的话,有些圆圈可能会漏掉。
6、Double param1:它表示传递给canny边缘检测算子的高阈值,而低阈值为高阈值的一半。
7、Double param2:投票数量阈值,它越小的话,就可以检测到更多根本不存在的圆,而它越大的话,能通过检测的圆就更加接近完美的圆形了。
8、Int minradius:最小半径
9、Int maxradius:最大半径
三、代码:
#include 
