重学数据结构与算法系列：链表及其应用

引言

链表是非常常用的基础数据结构，我们经常把它和数组放在一起进行比较。那我们首先来看下这两个常用的数据结构各自的特点是什么吧。

我们在实际编程的时候，如果进行数组的定义，那么就需要向系统申请连续的内存空间进行数据数据的存储。但是对于链表来说，它并不需要连续的内存空间。每个链表节点都存有指向下一个节点的地址，基于这种独特的数据结构，链表可以将不连续的内存区域串联起来进行数据存储。数据存储空间的连续与否是数组与链表数据结构最大的不同。

链表

本文主要给大家介绍下三种非常常见的链表结构，分别是单链表、循环链表以及双向链表。

单链表

就如上文讲述的那样，链表数据结构最大的特征就是可以将不连续的内存区域串联起来进行数据存储。链表中的每个节点实际就是内存区域的一块区域，他存储了节点的数据以及下一节点的地址信息。但是有两个各节点比较特殊，一个是头部节点，一个是尾部节点。头部节点是整个链表的初始位置，通过它来实现对于链表的访问。不过要注意的是头结点实际并不存储数据，它只包含了链表第一个节点的地址信息。

链表的操作主要包括了查找元素、添加元素以及删除元素等。对于数组的操作，由于它的内存区域是连续的，因此在进行增删操作的时候，为了保证数组的存储区域的连续，需要将数据进行整体的挪动，时间复杂度达到O（n）。

但是对于链表来说无论是添加还是删除元素，都不会涉及数据的整体移动，因此它的效率相对来说就会更加高一点。在删除元素的时候，只需要将上一节点的地址信息修改为下一节点的地址信息就完成了链表元素的删除动作。

 同样在进行链表元素的添加操作的时候，只要调整元素的地址信息指向新元素，同时将新元素的地址信息指向原来链表中的下一个节点元素，这样就完成了链表节点的添加操作。

 看上去好像很完美，但是在进行元素的查找操作的时候，就没有数组那么高效率了。大家可以从链表的数据结构特征中看的出来，如果要想访问链表中某个指定元素的话，必须要从链表的头部开始进行查找，一个一个去遍历，直到找到自己想要的元素

循环链表

循环链表可以说是一种特殊的单链表结构，那么它到底特殊在哪里呢？主要就是链表的最后一个节点不是指向null，而是指向链表的第一个节点，这就形成了一个环状结构。

双向链表

双向链表结构就稍微有点复杂了，他的数据节点中不仅包含了指向下一节点的next指针，还包含了指向前一节点的前置指针pre，因此称作为双向链表。由于增加了前置指针，双向链表需要更多的空间来进行数据存储，但是由于支持双向的数据查找，因此效率会更高点，这也是一种利用空间换时间的设计思路。

如何用链表实现LRU

上文我们对链表的数据结构进行了详细的说明，那么接下来就一起看看如何利用链表实现一个LRU。LRU的全称为Least Recently Used，它是一种内存数据淘汰算法。我们大家都知道内存大小是有限制的，如果无限制的往内存中塞数据，必定会导致内存数据暴涨而导致内存溢出最终引发平台异常。因此我们需要有对应的内存数据淘汰算法，将一些内存数据清除出去，确保内存不会被数据占满。

而常见的内存缓存淘汰算法有FIFO（First In，First Out）、最少使用策略 LFU（Least Frequently Used）、最近最少使用策略 LRU（Least Recently Used）。怎么理解这些缓存淘汰算法呢？实际上我用一个生活中的小例子说明下你就很容易理解了。我们家里面都有衣柜，有一天你发现衣柜快满了，你想清理一些衣服出去捐给希望工程。那么你该怎么选择需要被清理出去的衣服呢？一般我们的思路肯定就是把最旧的衣服（FIFO）、已经不怎么穿的衣服（LFU）的清理出去，同时会把一些最近不怎么穿（ LRU）的衣服放到其他的柜子中，而当前的这个柜子中永远放着当下经常穿的换洗衣服。你看，结合这个生活中最常见的例子是不是就很好理解这些看上去不明觉厉的缓存淘汰算法了。

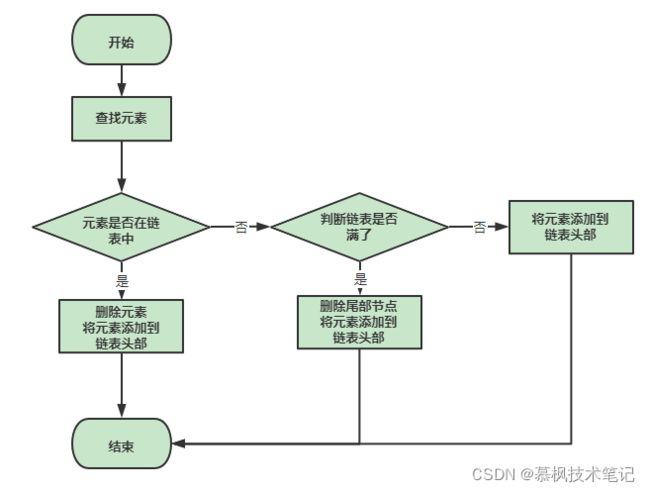
结合上文提到的链表数据结构，我们来考虑下LRU的实现方式。LRU的特点就是最少使用的进行删除，那么我们可以初始化一个指定大小的链表（类比具有固定大小的缓存），具体的实现的逻辑如下：

1、在这个链表当中，链表的尾部存放比较之前访问的元素，末尾节点就是最早访问过的元素；

2、当进行数据访问的时候，遍历链表进行查找，如该数据之前已经存在于链表中，那么就把当前接的节点进行删除，将该数据插入到链表的头部作为第一个节点；

3、如果遍历链表发现没有此数据，那么需要执行数据插入操作。在进行插入当前需要先检查下当前的链表的节点数是不是达到最大值了。如果达到最大值，需要对链表的末尾节点进行删除后再降数据插入到首位节点，如果链表节点个数没有达到最大值，那么可以直接将数据插入到链表的首位节点。

 下面结合双向链表以及HashMap实现了LRU的缓存功能，这也是面试中编码题目中经常会遇到的，大家务必要掌握。

这里使用了双向链表结合HashMap的方式实现LRU缓存数据淘汰，选择双向链表是为了可以加快数据的检索效率，而HashMap记录了数据在链表中的位置。通过这样的方式，我们可以通过HashMap进行节点的定位，迅速找出数据在链表中的位置，然后将其移动到双向链表的首部。这些操作可以在O（1）时间复杂度完成，提升了数据获取的效率。

/**
 * @Author: 慕枫技术笔记
 * @Date: 2022/3/9 07:39
 * @Version: V 1.0.0
 * @Description: LRU缓存淘汰
 */
public class LRUCache {
    
    class Node {
        String key;
        T value;
        Node prev;
        Node next;
        public Node() {}
        public Node(String key, T value) {this.key = key; this.value = value;}
    }

    //缓存数据节点
    private Map cache = new HashMap<>();
    private int size;
    private int capacity;
    private Node head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // 在添加节点和删除节点的时候进行边界检查
        head = new Node();
        tail = new Node();
        head.next = tail;
        tail.prev = head;
    }

    public T get(String key) {
        Node node = cache.get(key);
        if (node == null) {
            return null;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        moveToHead(node);
        return (T)node.value;
    }

    public void put(String key, T value) {
        Node node = cache.get(key);
        if (node == null) {
            // 如果 key 不存在，创建一个新的节点
            Node newNode = new Node(key, value);
            // 添加进HashMap缓存
            cache.put(key, newNode);
            // 需要添加到链表头部
            addToHead(newNode);
            ++size;
            //检查容量
            if (size > capacity) {
                // 如果超出，需要删除链表的末尾节点
                Node tail = removeTail();
                // 删除HashMap中对应的项

                cache.remove(tail.key);
                --size;
            }
        }
        else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;
            moveToHead(node);
        }
    }

    private void addToHead(Node node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(Node node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(Node node) {
        removeNode(node);
        addToHead(node);
    }

    private Node removeTail() {
        Node res = tail.prev;
        removeNode(res);
        return res;
    }

}