《数据结构》十道链表经典面试题多种方法深度解析
目录
⛰️一、题目解析
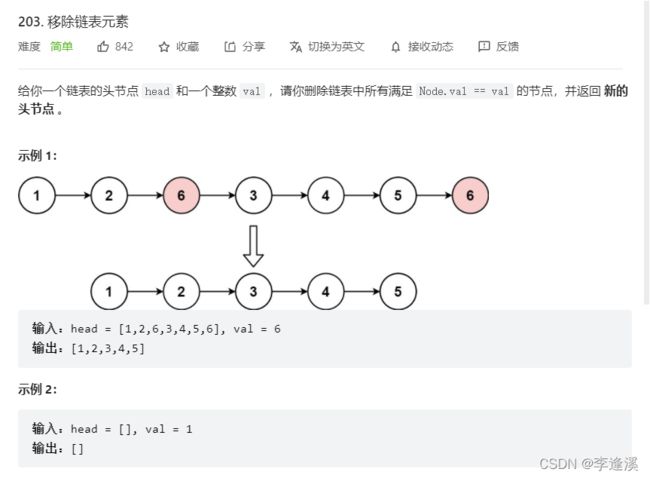
1.1删除链表中等于给定值 val 的所有节点(力扣)
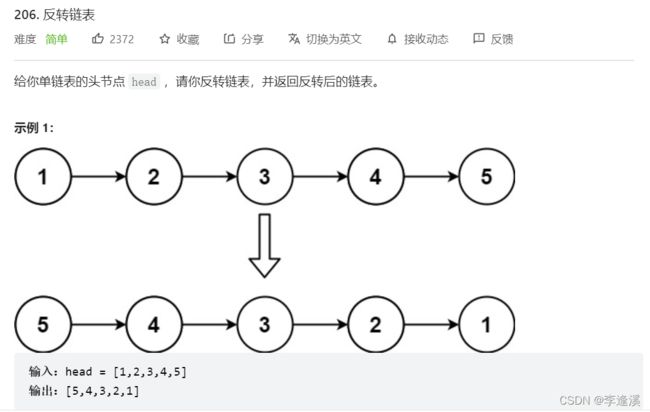
1.2反转一个单链表。(力扣)
1.3给定一个带有头结点 head 的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个 中间结点。(力扣)
1.4输出链表中倒数第k个结点。
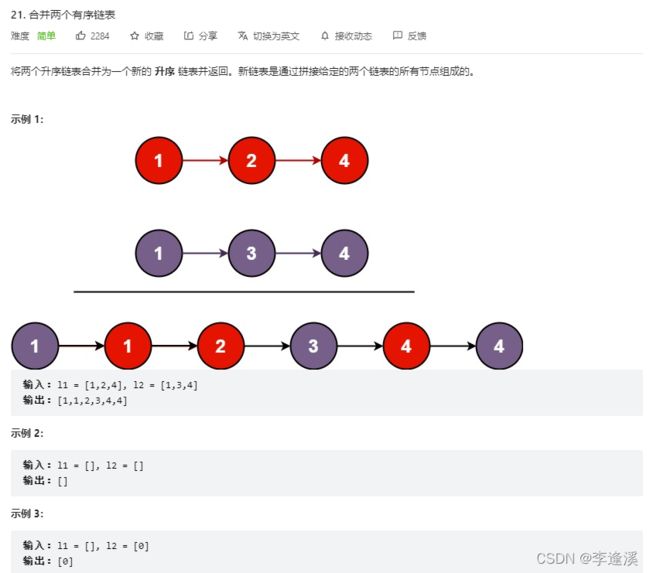
1.5将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
1.6编写代码,以给定值x为基准将链表分割成两部分,所有小于x的结点排在大于或等于x的结点之前 。
1.7 链表的回文结构
1.8输入两个链表,找出它们的第一个公共结点。
1.9给定一个链表,判断链表中是否有环。
1.10给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 NULL
⛰️一、题目解析
1.删除链表中等于给定值 val 的所有节点。2.反转一个单链表。3.给定一个带有头结点 head 的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个 中间结点。4.输出链表中倒数第k个结点。5.将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。6.编写代码,以给定值x为基准将链表分割成两部分,所有小于x的结点排在大于或等于x的结点之前 。7.链表的回文结构。8.输入两个链表,找出它们的第一个公共结点。9.给定一个链表,判断链表中是否有环。10.给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 NULL
1.1删除链表中等于给定值 val 的所有节点(力扣)
⚓思路一:剔除某些值,反之,保留某些值。
将不等于val的节点全都尾插至新的链表中,然后返回新的头节点。
细节:
新的链表尾指针需指向空
否则遇到1->2->3->6->5->8->6 val=6。这种情况会有问题。
因为tail的最后的指向是8,而8指向6,6指向空。
最后的错误输出是1->2->3->5->8->6。
解决:在cur退出循环的时候,将tail->next=NULL。但要保证前题tail不为空。
代码:
typedef struct ListNode ListNode;
struct ListNode* removeElements(struct ListNode* head, int val)
{
struct ListNode* newhead=NULL;
struct ListNode* newtail=NULL;
struct ListNode* cur=head;
while(cur)
{
if(cur->val!=val)
{
//将节点尾插至新链表
if(newhead==NULL)
{
newhead=newtail=cur;
}
else
{
newtail->next=cur;
newtail=cur;
}
}
cur=cur->next;
if(cur==NULL)
{
if(newtail)
newtail->next=NULL;
}
}
return newhead;
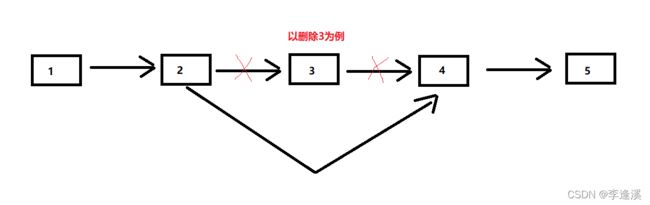
}⚓思路二:在原链表中操作,找到等于val值的节点,在删除它,这种删除就是把它前一个指针的指向后一个节点的地址。图解:细节:
当要删除的节点为头节点时,prev==NULL。
struct ListNode* temp=cur;
cur=cur->next;
prev->next=cur;(对空指针解引用,发生错误)。
free(temp);
解决:
分情况讨论,当要删除的节点是头节点时。执行以下操作。
cur=cur->next;
free(newhead);
newhead=cur;
代码:
typedef struct ListNode ListNode;
struct ListNode* removeElements(struct ListNode* head, int val)
{
if(head==NULL)
{
return head;
}
struct ListNode* prev=NULL;
struct ListNode* newhead=head;
struct ListNode* cur=head;
while(cur)
{
if(cur->val==val)
{
if(cur==newhead)
{
cur=cur->next;
free(newhead);
newhead=cur;
}
else
{
struct ListNode* temp=cur;
cur=cur->next;
prev->next=cur;
free(temp);
}
}
else
{
prev=cur;
cur=cur->next;
}
}
return newhead;
}1.2反转一个单链表。(力扣)
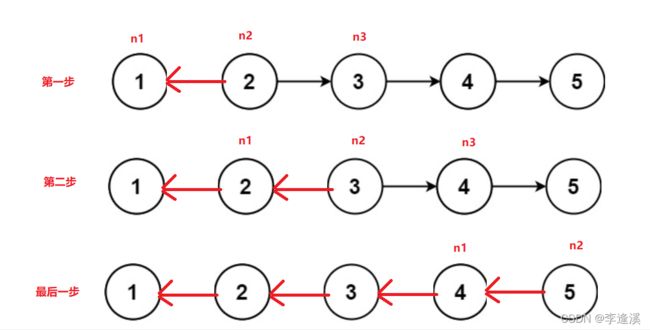
⚓思路一:
三指针法:前指针 中指针 后指针
翻转部分:中指针指向前指针
迭代部分:前指针=中指针;中指针=后指针;后指针=后指针->next。
图解:
细节:
最后循环的结束条件是n2==NULL。当n2是最后一个节点的地址时,n3是为空的。迭代部分将n3赋值给n2,此时再进行n3=n3->next显然是不合适的。
解决:
if(n3) n3=n3->next;
代码:
struct ListNode* reverseList(struct ListNode* head)
{
if(head==NULL)
{
return head;
}
struct ListNode* n1=NULL;
struct ListNode* n2=head;
struct ListNode* n3=head->next;
while(n2)
{
//翻转部分
n2->next=n1;
//迭代部分
n1=n2;
n2=n3;
if(n3)
n3=n3->next;
}
return n1;
}
⚓思路二:
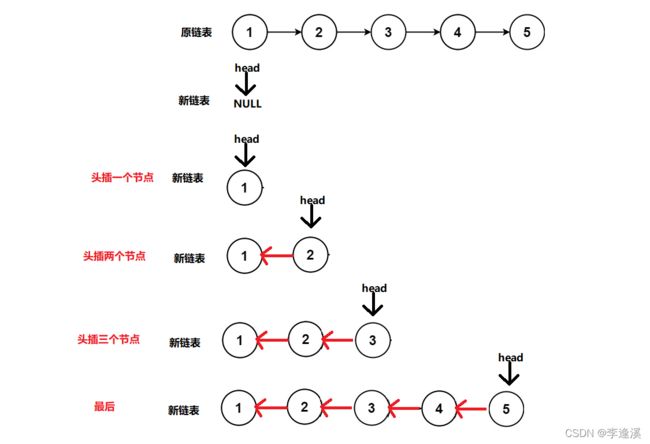
头插法:将原链表的节点头插至新链表,新链表初始为空。
图解:
代码:
struct ListNode* reverseList(struct ListNode* head)
{
struct ListNode* cur = head;
struct ListNode* newhead = NULL;
while(cur)
{
struct ListNode* next = cur->next;
cur->next = newhead;
newhead = cur;
cur = next;
}
return newhead;
}1.3给定一个带有头结点 head 的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个 中间结点。(力扣)
⚓思路一:
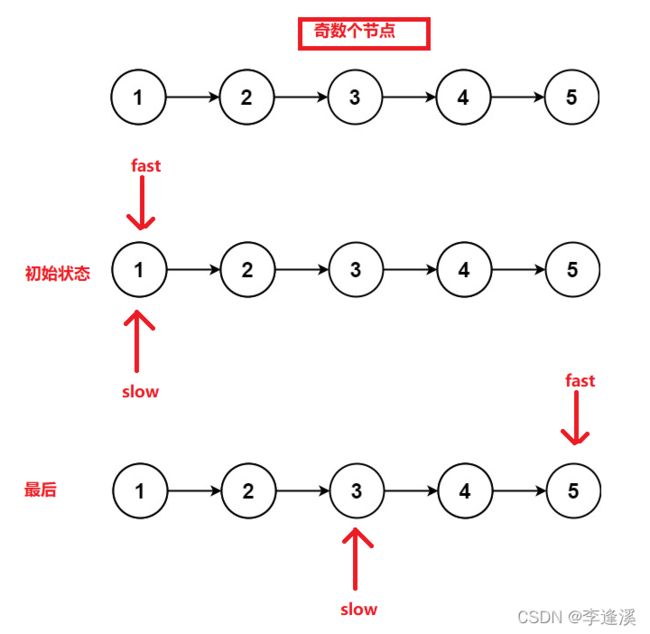
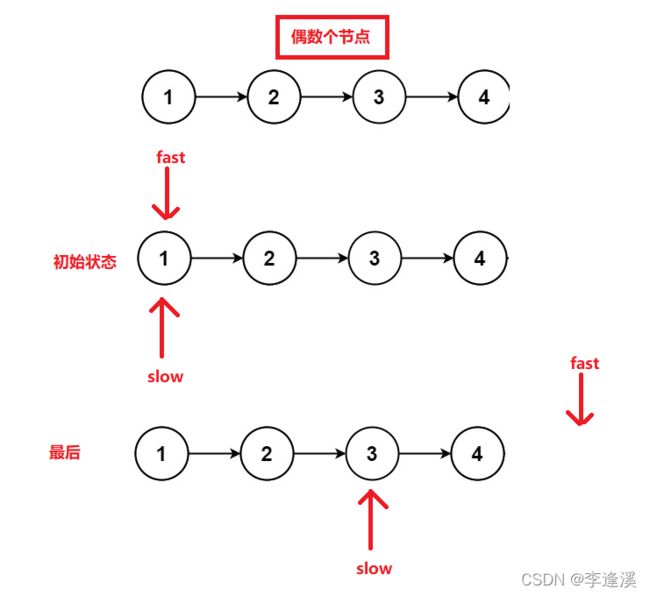
快慢指针:一个快指针(fast),一个慢指针(slow)。初始状态它们都指向空,快指针一次走两步,慢指针一次走一步。当节点数为偶数时,快指针走到NULL时,slow就是中间节点,当节点数为奇数时,快指针走到最后一个节点时,slow就是中间节点。
图解:
代码:
struct ListNode* middleNode(struct ListNode* head)
{
if(head==NULL)
{
return head;
}
struct ListNode* fast=head;
struct ListNode* slow=head;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
}
return slow;
}⚓思路二:
求总链表长度,取一个cur指针,它初始指向head,走总链表长度/2的步数即到达中间节点。
1.4输出链表中倒数第k个结点。
⚓思路一:
快慢指针:一个快指针(fast),一个慢指针(slow),起初它们都指向head。先让fast走k步,此时它们之间的距离就是k,在同时让快指针走一步,慢指针走一步,当快指针走到NULL时,slow即为倒数第k个节点。
细节:
当输入的k大于节点个数时,会出现fast越界的问题。
解决:
在fast移动之前判断fast是否为空,如果为空则返回NULL,不为空就向后移动。
代码:
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{
if(pListHead==NULL)
{
return NULL;
}
struct ListNode* prev=pListHead;
struct ListNode* cur=pListHead;
while(k--)
{
if(cur)
cur=cur->next;
else
{
return NULL;
}
}
while(cur)
{
cur=cur->next;
prev=prev->next;
}
return prev;
}1.5将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
⚓思路一:
归并思想:取一个初始为空的新链表,比较指向list1和指向list2的节点值,小的先放入新链表,放完之后,小的节点指针向后移动。当有一个指针为空时,就将另一个链表直接连接至新链表。
代码:
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
if(list1==NULL)
{
return list2;
}
if(list2==NULL)
{
return list1;
}
struct ListNode* cur1=list1;
struct ListNode* cur2=list2;
struct ListNode* newhead=(struct ListNode*)malloc(sizeof(struct ListNode));
struct ListNode* tail=newhead;
while(cur1 && cur2)
{
if(cur1->val>cur2->val)
{
tail->next=cur2;
tail=cur2;
cur2=cur2->next;
}
else
{
tail->next=cur1;
tail=cur1;
cur1=cur1->next;
}
}
if(cur1)
{
tail->next=cur1;
}
else
{
tail->next=cur2;
}
return newhead->next;
}1.6编写代码,以给定值x为基准将链表分割成两部分,所有小于x的结点排在大于或等于x的结点之前 。
⚓思路一:
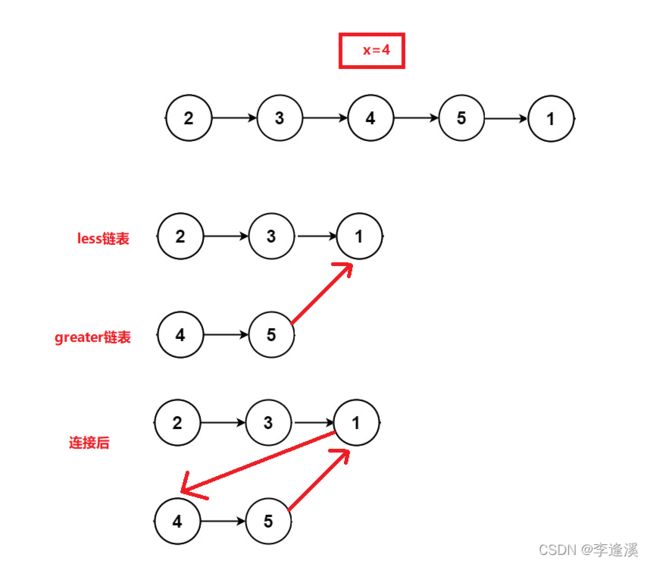
取新链表less和新链表greater,它们初始都为空。然后用指针cur遍历一遍原链表,小于x的节点放入less链表中,大于x的放入greater链表中,最后再将less和greater连接起来,返回less的头指针。
细节:
小于x的节点放less链表中,不要写成小于等于x的节点放入less链表中。
当less为空时,返回greater的头指针。
当less不为空时,less最后的节点要指向greater的头节点。并且将greater最后节点的指针指向空。因为greater最后的指向可能指向less的某个节点,连接less和greater的时候就会形成环。
图解:
代码:
class Partition {
public:
ListNode* partition(ListNode* pHead, int x)
{
ListNode* less=NULL;
ListNode* lesstail=NULL;
ListNode* greater=NULL;
ListNode* greatertail=NULL;
ListNode* cur=pHead;
while(cur)
{
if(cur->valnext=cur;
lesstail=cur;
}
}
else
{
if(greater==NULL)
{
greater=greatertail=cur;
}
else
{
greatertail->next=cur;
greatertail=cur;
}
}
cur=cur->next;
}
if(less)
{
lesstail->next=greater;
if(greatertail)
{
greatertail->next=NULL;
}
return less;
}
else
{
return greater;
}
}
}; 1.7 链表的回文结构
什么是回文结构?就是正着读和反着读没区别,即对称的图形。
比如1->2->3->2->1。该结构就是回文结构。
⚓思路一:
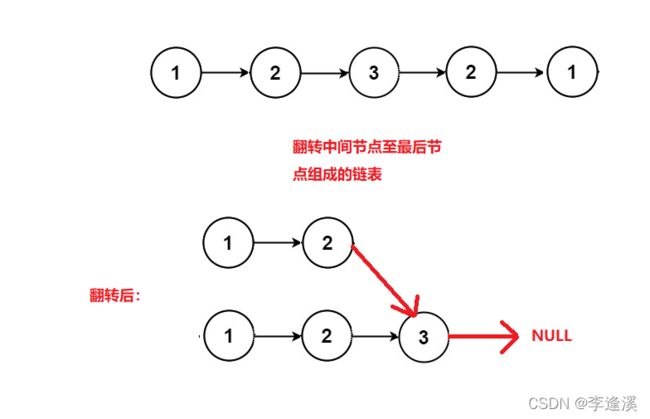
找中间节点,然后翻转中间节点至最后节点组成的链表
图解:
如果head1链表和head2链表一致则说明该链表是回文结构。
结束条件是:head2==NULL。
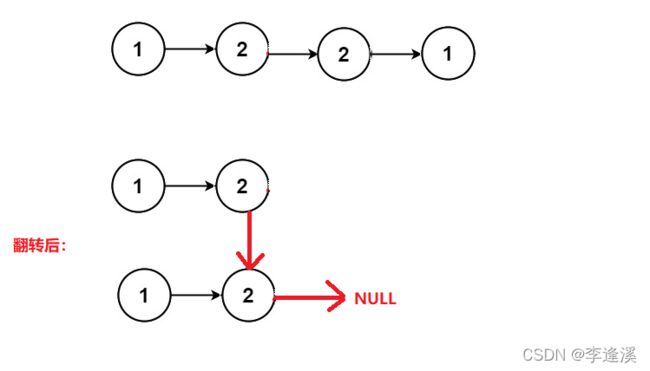
偶数个节点情况:
与奇数个链表的情况结束条件一致。
代码:
class PalindromeList {
public:
bool chkPalindrome(ListNode* A)
{
//找中间节点
ListNode* slow=A;
ListNode* fast=A;
ListNode* mid=NULL;
ListNode* head1=A;
ListNode* head2=NULL;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
}
mid = slow;
//逆置mid-NULL各节点(核心)
ListNode* n1=NULL;
ListNode* n2=mid;
ListNode* n3=mid->next;
while(n2)
{
n2->next=n1;
n1=n2;
n2=n3;
if(n3)
n3=n3->next;
}
head2=n1;
//判断是否回文
while(head2)
{
if(head1->val != head2->val)
{
return false;
}
head1=head1->next;
head2=head2->next;
}
return true;
}
};
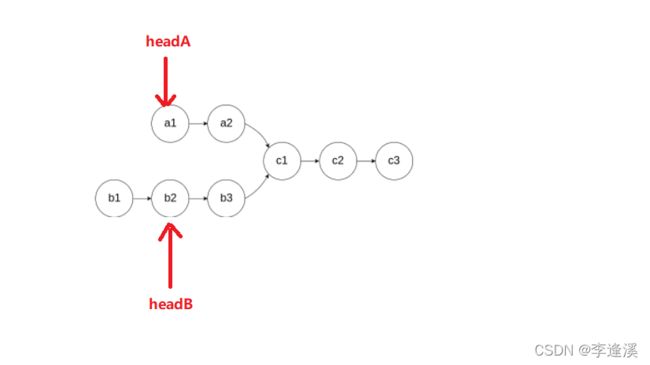
1.8输入两个链表,找出它们的第一个公共结点。
⚓思路一:
先判断是否存在交点,判断方法如下:
当A和B有相同的尾节点,则说明A和B有交点。
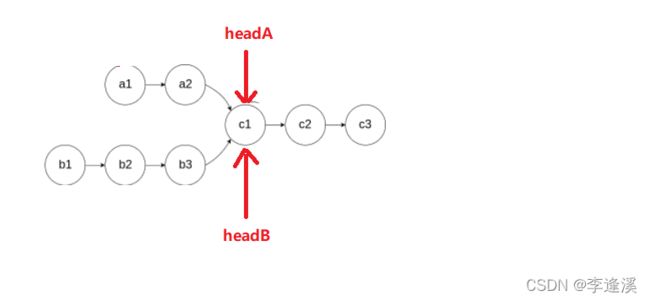
当存在交点时,让长的链表(图B)先走A和B链表长度的差距步,然后让A和B同时走,直到指针A等于指针B,此时指针A就是交点的地址。
图解:
先让headB走差距步,即走1步。
让headA和heaB同时走,直到headA等于headB,此时headA就是交点的地址。
代码:
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
ListNode* list1_tail=headA;
ListNode* list2_tail=headB;
ListNode* greater=headA;
ListNode* less=headB;
int lenA=1;
int lenB=1;
//判断是否有交点的核心思想:尾部节点的地址一致。
while(list1_tail->next)
{
list1_tail=list1_tail->next;
lenA++;
}
while(list2_tail->next)
{
list2_tail=list2_tail->next;
lenB++;
}
if(list1_tail!=list2_tail)
{
return NULL;
}
//找交点
int gap=abs(lenA-lenB);
if(lenAnext;
}
while(greater && less)
{
if(greater == less)
{
return less;
}
greater=greater->next;
less=less->next;
}
return NULL;
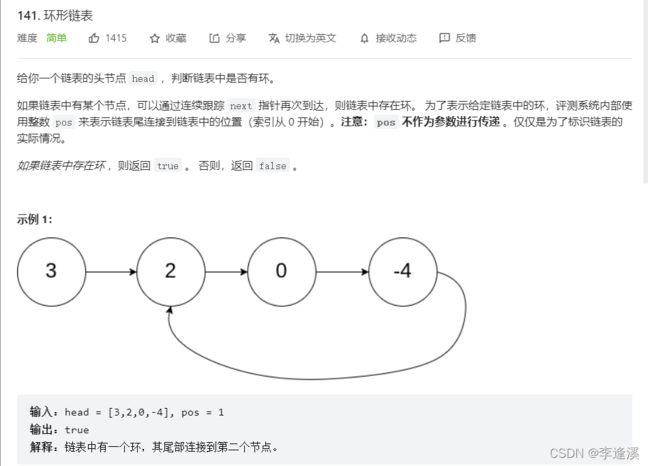
} 1.9给定一个链表,判断链表中是否有环。
⚓思路一:
快慢指针:定义两个指针,一个快指针(fast),一个慢指针(slow),初始它们都指向头节点,快指针一次走两步,慢指针一次走一步,如果有环,则快指针必定与慢指针在环的某个节点处相遇。无环,则它们绝对不会相遇。
细节:
while(fast && fast->next) { slow=slow->next; fast=fast->next->next; if(slow==fast) { return true; } }能这样写吗?
不能,因为初始值slow和fast是相等的,直接就return true了。
正确写法:
while(fast && fast->next) { slow=slow->next; fast=fast->next->next; if(slow==fast) { return true; } }讨论:
如果fast一次走两步,slow一次走一步,它们一次会相遇吗?
如果fast一次走3步,slow一次走1步,它们一次会相遇吗?
如果fast一次走4步,slow一次走一步,它们一次会相遇吗?
代妈:
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head)
{
ListNode* slow=head;
ListNode* fast=head;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
return true;
}
}
return false;
}
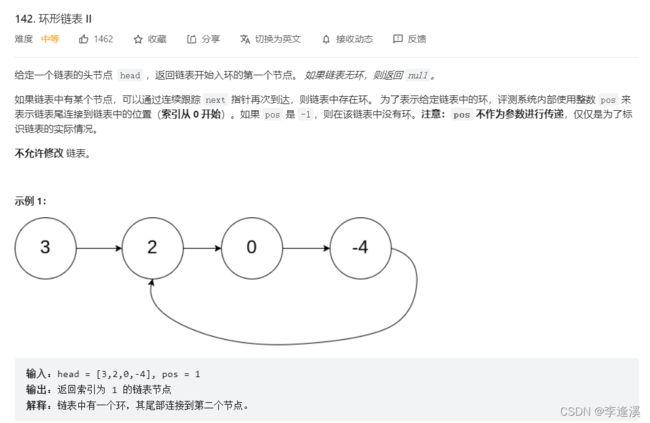
1.10给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 NULL
⚓思路一:
先判断是否有环,使用快慢指针的方法。
如果有环,则记录快指针和慢指针相遇的节点地址。
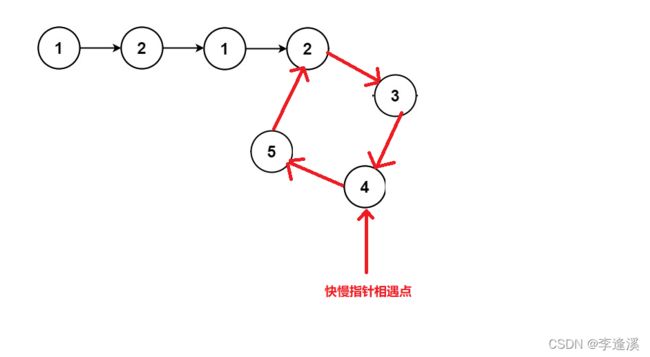
假设在值为4的位置快慢指针相遇,我们让mee指向相遇点。
此时我们做如下操作:
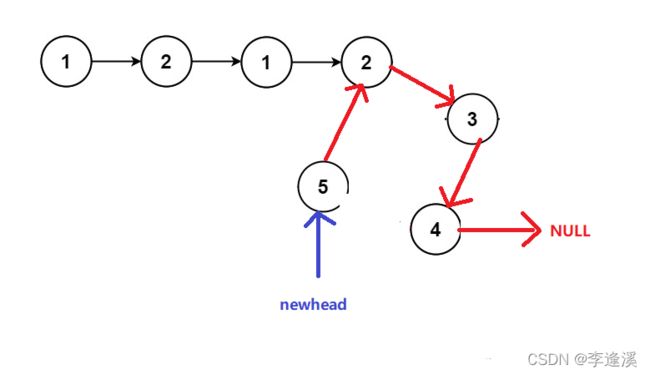
newhead=meet->next(让newhead指向值为5的这一节点)。
然后mee->next=NULL。(让meet指向空)。
此时图转化为:
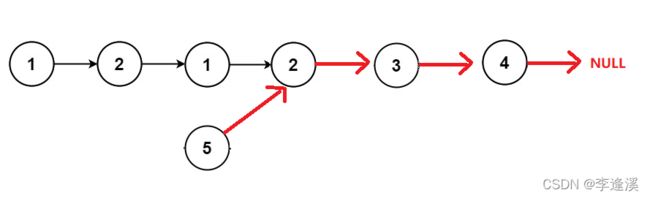
我们调整一下图
我们要找的环入口就是head和newhead两链表的相交点。
与题1.8解法一致。
代码:
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
ListNode* list1_tail=headA;
ListNode* list2_tail=headB;
ListNode* greater=headA;
ListNode* less=headB;
int lenA=1;
int lenB=1;
//判断是否有交点的核心思想:尾部节点的地址一致。
while(list1_tail->next)
{
list1_tail=list1_tail->next;
lenA++;
}
while(list2_tail->next)
{
list2_tail=list2_tail->next;
lenB++;
}
if(list1_tail!=list2_tail)
{
return NULL;
}
//找交点
int gap=abs(lenA-lenB);
if(lenAnext;
}
while(greater && less)
{
if(greater == less)
{
return less;
}
greater=greater->next;
less=less->next;
}
return NULL;
}
struct ListNode *detectCycle(struct ListNode *head)
{
ListNode* slow=head;
ListNode* fast=head;
ListNode* meet=NULL;
ListNode* head1=head;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
meet=fast;
//找交点,即链表head1和链表head2的公共节点。
ListNode* head2=meet->next;
meet->next=NULL;
return getIntersectionNode(head1,head2);
}
}
return NULL;
} ⚓思路二:
数学推理法:与思路一相同,先用快慢指针判断是否出现环,如果无环,直接返回NULL,如果有环,则记录快慢指针的相遇点。
设从头节点到环的入口点的步数为L,环的长度为C。
假设环入口点走x步快慢指针相遇了。
可得出:
慢指针走的路程为:L+X。
快指针走的路程为:L+X+C*N(其中N代表圈数,N>=1)。
快指针路程是慢指针路程的两倍
所以:L+X+C*N=2*(L+X)。
化简得:L=C*N-X
L=C*(N-1)+C-X。
因此我们只需要让一个指针从head走,另一个指针从meet走,当两指针相等时,它们就指向环的入口点。
代码:
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head)
{
ListNode* slow=head;
ListNode* fast=head;
ListNode* cross_point=NULL;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
cross_point=slow;
while(cross_point!=head)
{
head=head->next;
cross_point=cross_point->next;
}
return cross_point;
}
}
return NULL;
}