【理解】经典角点检测算法--Harris角点
目录
-
-
- 什么是角点
- 角点检测算法的原始思想:
- Harris角点检测原理
- Harris角点算法的基本步骤
- 实践:
-
- Harris角点检测可能会用到的OpenCV API:
- 手写API:
-
- 1.展示图片:
- 2.手写Harris特征:
- 3.手写非极大值抑制:
- 4.在原图标注角点:
- 5.响应值颜色渐变(为了美观,没什么用)
- 6.滑动窗口:
- 7.Harris角点检测回调函数:
- main:
- 实现效果:
-
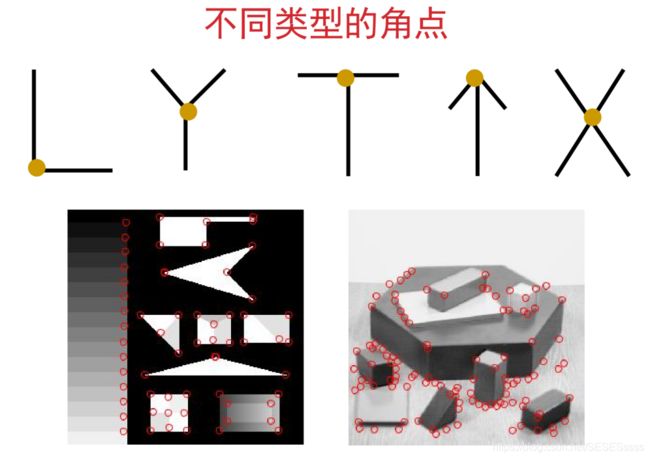
什么是角点
角点还没有明确的数学定义,但普遍具有以下特征:
角点检测算法的原始思想:
我们可以从角点具有的特征出发:
即选取一个局部窗口,将这个窗口沿着各个方向移动,计算移动前后窗口内像素的差异的多少进而判断窗口对应的区域是否是角点。
有了基本的对角点的描述思想,我们可以进一步把它转化为数学描述:

通过数学描述,我们可以总结出Harris角点的特征:
但事实上,如果我们此时用以上公式进行角点检测,会发现其中的参数u和v没有明确的规定,也就是窗口移动的方向。
●所以我们也可以人为规定u和v,但这样一来,指定方向窗口滑动又可能导致检测出来的角点其实是边缘点;
●所有我们可以指定若干组的u和v,即不同的窗口滑动方向,对所有的u和v求得E再进行加权平均,完美。
然而事实上Harris角点检测并没有这么做。
Harris可能在想,我应该如何优化这个原始的检测函数呢,提高精度,降低算法的复杂度呢?
Harris角点检测原理
这时候就要用到数学工具:
对于不同区域的图像灰度梯度:

不同区域的图像灰度梯度分布:
当图像中灰度变化较为平坦时,Ix和Iy集中分布在原点附近
当图像中存在边缘点时,x和y其中一方具有较大的梯度
当图像中存在角点时,x和y都具有较大的梯度

![]()

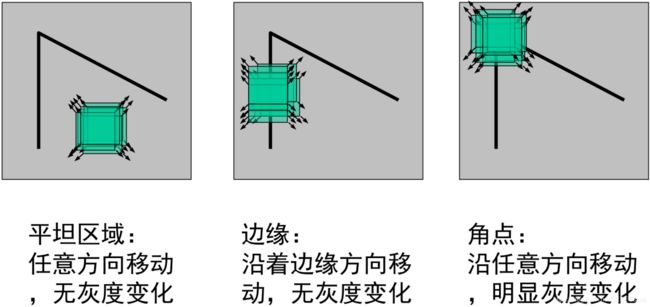
平坦区域:两个特征值都小,且近似相等,能量函数在各个方向上都较小;
边缘区域:一个特征值大,另一个特征值小,能量函数在某一方向上增大,其他方向较小;
角点区域:两个特征值都大,且近似相等,能量函数在所有方向上都增大。
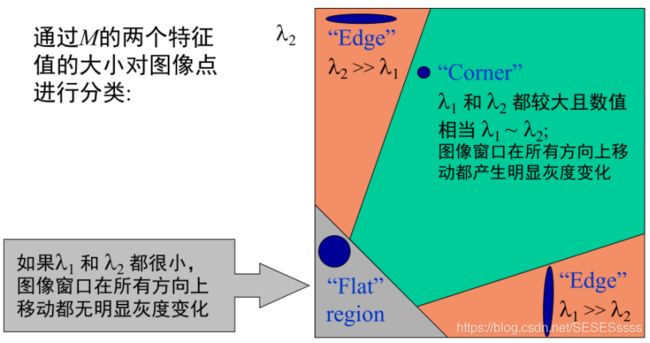
这样一来,我们就可以仅通过矩阵M的特征值,来评估图像是否存在角点
但Harris角点的计算方法甚至不需要用到特征值,只需要计算一个Harris响应值R:

而对于n阶方阵又有以下性质:
行列式等于特征值之和;
迹等于特征值之积。
这样一来就避免单独求出特征值:

到此,通过求出R,我们便可以进行角点检测。(你会发现最后根本不需要代入u,v进行计算)
Harris角点算法的基本步骤
根据上述的讨论,我们总结出Harris角点算法的基本步骤:
- 计算窗口中各像素点在x和y方向的梯度;
- 计算两个方向梯度的乘积,即Ix ^ 2 , Iy ^ 2 , IxIy(可以用一些一阶梯度算子求得图像梯度)
- 使用滤波核对窗口中的每一像素进行加权,生成矩阵M和元素A,B,C
- 计算每个像素的Harris响应值R,并对小于某阈值T的R置0;
- 由于角点所在区域的一定邻域内都有可能被检测为角点,所以为了防止角点聚集,最后在3×33×3或5×55×5的邻域内进行非极大值抑制,局部最大值点即为图像中的角点。
实践:
Harris角点检测可能会用到的OpenCV API:
normalize(),归一化函数Sobel(),Sobel算子,求图像梯度cornerHarris(), OpenCV的Harris角点检测APIcreateTrackbar(),添加滑动窗口convertScaleAbs(),图像的线性变换:

手写API:
bool Pic_show(Mat src,const char *param); //展示图片
void Harris_threshold_arrange(); //滑动窗口
void Harris_detaction(int, void*); //Harris角点检测回调函数
void draw_Point(Mat src,Mat SRC,int T); //在原图标注角点
void Gradient_change(Mat src); //响应值颜色渐变(channel:B0,G1,R2)
void My_cornerHarris(Mat src, Mat& dst, int ksize, double k); //手写Harris特征
void NMF(Mat &src); //手写非极大值抑制
1.展示图片:
bool Pic_show(Mat src,const char *param) //展示图片
{
if(src.empty()) {
cout<<"图片打开失败!\n";
return false;
}
else imshow(param,src);
waitKey(0);
return true;
}
2.手写Harris特征:
void My_cornerHarris(Mat src, Mat& dst, int ksize, double k) //手写Harris特征
{
Mat Ix, Iy; //存储图像一阶梯度
Mat M(src.size(),CV_32FC3); //创建3通道矩阵M存储 Ix*Ix , Ix*Iy , Iy*Iy
Mat R(src.size(),CV_32FC1); //创建3通道矩阵R存储Harris响应值
//使用Sobel算子提取图像x方向梯度和y方向梯度
Sobel(src,Ix,CV_32FC1,1,0,ksize);
Sobel(src,Iy,CV_32FC1,0,1,ksize);
//存储Ix*Ix , Ix*Iy , Iy*Iy
for(int i = 0;i<src.rows;i++){
for(int j = 0;j<src.cols;j++){
M.at<Vec3f>(i,j)[0]= Ix.at<float>(i,j)*Ix.at<float>(i,j); //Ix*Ix
M.at<Vec3f>(i,j)[1]= Ix.at<float>(i,j)*Iy.at<float>(i,j); //Ix*Iy
M.at<Vec3f>(i,j)[2]= Iy.at<float>(i,j)*Iy.at<float>(i,j); //Iy*Iy
}
}
//高斯滤波对M矩阵进行加权求和
GaussianBlur(M, M, Size(ksize, ksize),2,2);
//求得Harris响应值
for(int i = 0;i<src.rows;i++){
for(int j = 0;j<src.cols;j++){
float A = M.at<Vec3f>(i,j)[0]; //Ix*Ix
float C = M.at<Vec3f>(i,j)[1]; //Ix*Iy
float B = M.at<Vec3f>(i,j)[2]; //Iy*Iy
//响应值计算公式
R.at<float>(i,j) = (A*B - C*C) - (k*( A+B )*( A+B ));
}
}
dst = R.clone();
}
3.手写非极大值抑制:
void NMS(Mat &src) //手写非极大值抑制
{
int i,j,k,l,cnt=0;
//遍历图像
for(i = 2;i<src.rows;i++)
for(j = 2;j<src.cols;j++)
//采用5×5窗口,小于中心像素置零
for(k=i-2;k<=i+2;k++)
for(l = j-2; l<=j+2;l++)
if(src.at<float>(k,l)<=src.at<float>(i,j) && k!=i && l!=j && src.at<float>(k,l)>0)
src.at<float>(i,j) = 0;
}
4.在原图标注角点:
void draw_Point(Mat src,Mat SRC,int T) //在原图标注角点
{
cvtColor(SRC,DST,CV_GRAY2BGR);
int Num_of_corner = 0;
for(int row=0;row<src.rows;row++){
uchar* Currunt_row = src.ptr(row); //行指针
for(int col = 0;col<src.cols;col++){
int R_value = Currunt_row[col]; //提取处理后的角点响应
if(R_value >= T){
//颜色渐变
Num_of_corner++; //计算角点数
int R,G,B;
if(R_value<=63.75){
B = 255;
G = int(255*R_value/63.75);
R = 0;
circle(DST,Point(col,row),3,Scalar(B,G,R),1,LINE_MAX); //圈出大于阈值的角点
}
else if(R_value<=127.5){
B = 255-int(255*(R_value-63.75)/63.75);
G = 255;
R = 0;
circle(DST,Point(col,row),3,Scalar(B,G,R),1,LINE_MAX); //圈出大于阈值的角点
}
else if(R_value<=191.25){
B = 0;
G = 255;
R = int(255*(R_value-127.5)/63.75);
circle(DST,Point(col,row),3,Scalar(B,G,R),1,LINE_MAX); //圈出大于阈值的角点
}
else if(R_value<=255){
B = 0;
G = 255-saturate_cast<uchar>(255*(R_value-191.25)/63.75);
R = 255;
circle(DST,Point(col,row),3,Scalar(B,G,R),1,LINE_MAX); //圈出大于阈值的角点
}
}
}
Currunt_row++;
}
cout<<"total nums of corner is:"<<Num_of_corner<<endl;
}
5.响应值颜色渐变(为了美观,没什么用)
void Gradient_change(Mat src) //通道阈值渐变(channel:B0,G1,R2)
{
Mat dst = Mat::zeros(src.size(),CV_8UC3);
for(int row=0;row<src.rows;row++){
for(int col=0;col<src.cols;col++){
int BGR_value = src.at<uchar>(row,col); //三通道像素指针(RGB)
if(BGR_value<=63.75){
dst.at<Vec3b>(row,col)[0]= 255;
dst.at<Vec3b>(row,col)[1]= int(255*BGR_value/63.75);
dst.at<Vec3b>(row,col)[2]= 0;
}
else if(BGR_value<=127.5){
dst.at<Vec3b>(row,col)[0]= 255-int(255*(BGR_value-63.75)/63.75);
dst.at<Vec3b>(row,col)[1]= 255;
dst.at<Vec3b>(row,col)[2]= 0;
}
else if(BGR_value<=191.25){
dst.at<Vec3b>(row,col)[0]= 0;
dst.at<Vec3b>(row,col)[1]= 255;
dst.at<Vec3b>(row,col)[2]= int(255*(BGR_value-127.5)/63.75);
}
else if(BGR_value<=255){
dst.at<Vec3b>(row,col)[0]= 0;
dst.at<Vec3b>(row,col)[1]= 255-saturate_cast<uchar>(255*(BGR_value-191.25)/63.75);
dst.at<Vec3b>(row,col)[2]= 255;
}
}
}
imshow("My_Gradient_change",dst);
}
6.滑动窗口:
int Threshold = 172;
int K = 400;
void Harris_threshold_arrange() //滑动窗口
{
namedWindow("Harris_detaction",CV_WINDOW_NORMAL);
Harris_detaction(0,0);
createTrackbar("T_value","Harris_detaction",&Threshold,255,Harris_detaction); //阈值T
createTrackbar("k_value","Harris_detaction",&K,700,Harris_detaction); //阈值k
waitKey(0);
}
7.Harris角点检测回调函数:
void Harris_detaction(int, void*) //Harris角点检测回调函数
{
Mat dst = Mat::zeros(SRC.size(), CV_32FC1);
int blockSize = 2; //矩阵M的维数(二维以上的原理不太清楚)
int ksize = 3; //窗口大小
double k = K*0.0001; //阈值k
//求出每一个像素点的Harris响应值(使用OpenCV API)
//cornerHarris(SRC, dst,blockSize, ksize, k);
My_cornerHarris(SRC, dst, ksize, k);
NMS(dst); //手写非极大值抑制
normalize(dst,dst,0,255,NORM_MINMAX,CV_32FC1,Mat());//将Harris响应值归一化
convertScaleAbs(dst,dst,1,0); //将Harris响应值转为整型(uchar)
Gradient_change(dst); //绘制角点响应分布图(渐变)
imshow("Harris_callback",dst); //角点响应分布图
draw_Point(dst,SRC,Threshold); //在原图标注角点
imshow("Harris_detaction",DST); //result
}
main:
int main()
{
Mat src = imread("test13.jpg",1);
Pic_show(src,"input");
cvtColor(src,SRC,CV_BGR2GRAY);
Harris_threshold_arrange();
//resize(src,DST,Size(1404,648));
//imwrite("test13.jpg",DST);
}
实现效果:
左 with NMS ,右 without NMS:
在角点数量相似的情况下,通过非极大值抑制能使角点较为分散。
归一化后的Harris响应图:


参考:
Harris角点检测原理详解
Harris角点详细解释
Harris角点检测原论文:
http://www.bmva.org/bmvc/1988/avc-88-023.pdf