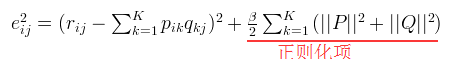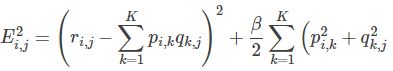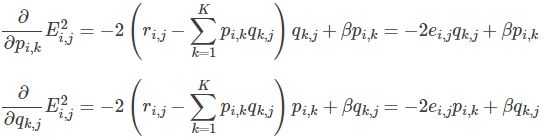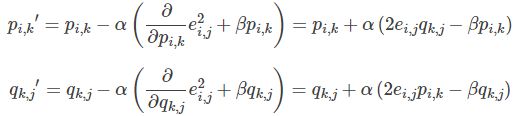矩阵分解
MF
有如下R(5,4)的打分矩阵：（“-”表示用户没有打分）
其中打分矩阵R(n,m)是n行和m列，n表示user个数，m行表示item个数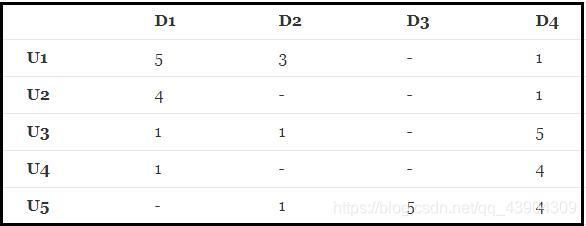
那么，如何根据目前的矩阵R（5,4）如何对未打分的商品进行评分的预测（如何得到分值为0的用户的打分值）？
——矩阵分解的思想可以解决这个问题，其实这种思想可以看作是有监督的机器学习问题（回归问题）。
矩阵R可以近似表示为P与Q的乘积：R（n,m）≈ P(n,K)*Q(K,m)
矩阵分解的过程中，将原始的评分矩阵
分解成两个矩阵
和
的乘积： 
矩阵P(n,K)表示n个user和K个特征之间的关系矩阵，这K个特征是一个中间变量，矩阵Q(K,m)的转置是矩阵Q(m,K)，矩阵Q(m,K)表示m个item和K个特征之间的关系矩阵，这里的K值是自己控制的，可以使用交叉验证的方法获得最佳的K值。为了得到近似的R(n,m)，必须求出矩阵P和Q，如何求它们呢？
【方法】
-
首先令
-
损失函数：使用原始的评分矩阵
与重新构建的评分矩阵
之间的误差的平方作为损失函数，即：如果R(i,j)已知，则R(i,j)的误差平方和为：
最终，需要求解所有的非“-”项的损失之和的最小值：
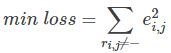
3. 使用梯度下降法获得修正的p和q分量：
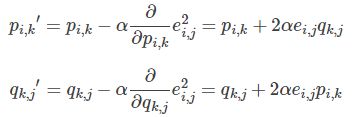
4. 不停迭代直到算法最终收敛（直到sum(e^2) <=阈值）
（Plus：为了防止过拟合，增加正则化项）
【加入正则项的损失函数求解】
-
首先令
-
通常在求解的过程中，为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束，加入正则的损失函数为：
也即：
- 使用梯度下降法获得修正的p和q分量：
求解损失函数的负梯度：
根据负梯度的方向更新变量：
- 不停迭代直到算法最终收敛（直到sum(e^2) <=阈值）
【预测】利用上述的过程，我们可以得到矩阵和，这样便可以为用户 i 对商品 j 进行打分：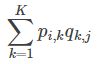
import numpy as np
from math import pow
import matplotlib.pyplot as plt
R=np.array([[5,3,0,1],[4,0,0,1],[1,1,0,5],[1,0,0,4],[0,1,5,4]])
print("原始的评分矩阵R为：")
print(R)
alpha=0.0002#学习率
beta=0.02
N=len(R)
M=len(R[0])
K=2
P=np.random.rand(N,K)#生成N行K列的矩阵
Q=np.random.rand(K,M)#生成K行M列的矩阵
result=[]
for i in range(5000):#运行5000次
for i in range(len(R)):
for j in range(len(R[i])):
if R[i][j]>0:
eij=R[i][j]-np.dot(P[i,:],Q[:,j])
for k in range(K):
P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
eR=np.dot(P,Q)#填充后的矩阵
e=0#误差
for i in range(len(R)):
for j in range(len(R[i])):
if R[i][j]>0:
e = e + pow(R[i][j] - np.dot(P[i, :], Q[:, j]), 2)
for k in range(K):
e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
result.append(e)
if e<0.001:
break
print("经过填充后的矩阵eR:")
print(eR)
n = len(result)
x = range(n)
print(x)
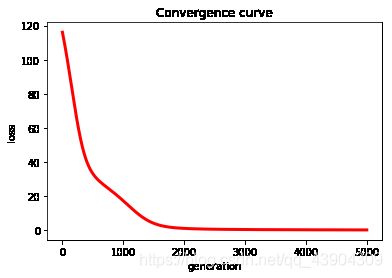
plt.plot(x, result, color='r', linewidth=3)
plt.title("Convergence curve")
plt.xlabel("generation")
plt.ylabel("loss")
plt.show()
结果
原始的评分矩阵R为：
[[5 3 0 1]
[4 0 0 1]
[1 1 0 5]
[1 0 0 4]
[0 1 5 4]]
经过填充后的矩阵eR:
[[4.99624873 2.93544304 4.48473294 0.99914131]
[3.96256443 2.3373952 3.7417222 0.99661392]
[1.06212841 0.83976764 5.25422718 4.96327875]
[0.96875908 0.74074439 4.28993813 3.97199539]
[1.76812146 1.20587323 4.91735138 4.03231098]]
结果图
